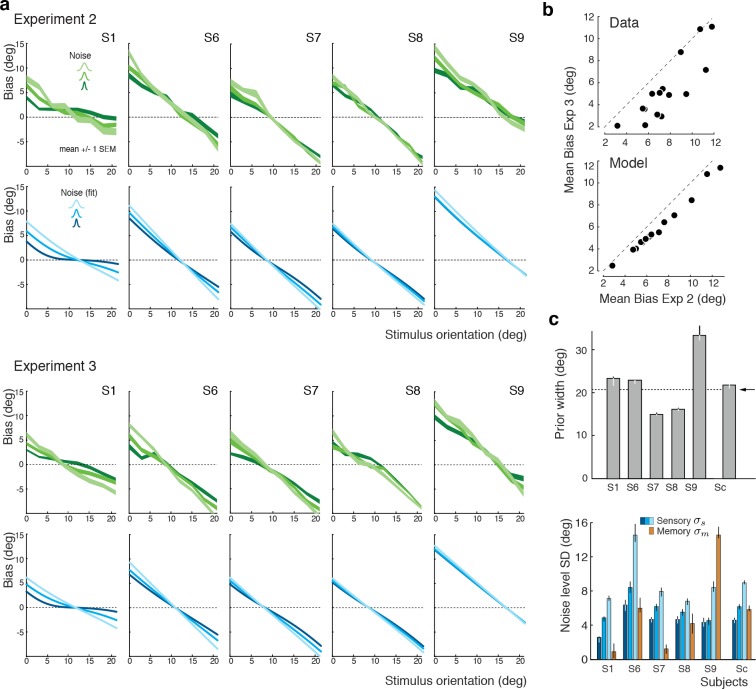
Figure 7. Experiments 2 and 3: Joint fit to data for individual subjects.

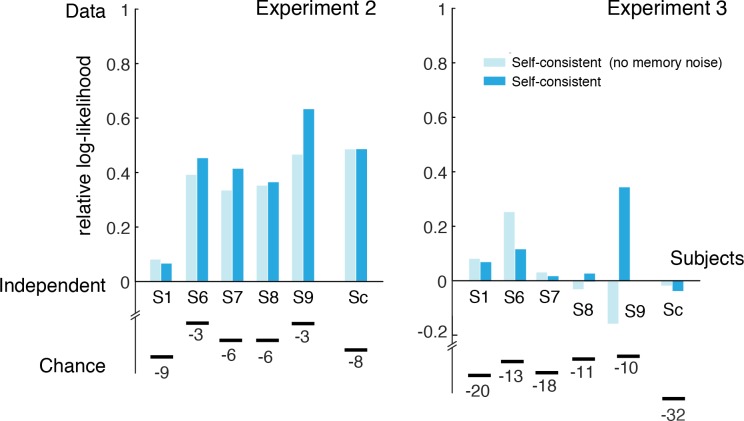
(a) Five subjects (S1, S6-9) participated both in Exp. 2 and 3. We performed a joint model fit to the data from both experiments for every subject. Each column shows data (green curves) and fit (blue curves) for a particular subject. As in Exp. 1, the bias pattern across subjects shows substantial variability yet is strikingly similar between the two experiments. (b) Comparing the mean biases observed in Exps. 2 and 3 reveals that biases in Exp. 3 are slightly smaller for stimulus orientations close to the boundary. This effect is predicted by the model. (c) Fit prior widths $w_p$ and noise levels for individual subjects and the combined subject. Subjects’ priors were closer to the experimental distribution than in Exp. 1 because in Exps. 2 and 3 subjects were reminded about the stimulus range at the beginning of each trial. Noise levels were comparable to those in Exp. 1 (for S1 we jointly fit data from all three experiments). Errorbars indicated the 95% confidence interval over 100 bootstrapped samples of the data. See Figure 7—figure supplement 1 for a goodness-of-fit analysis.

Figure 7—figure supplement 1. Goodness-of-fits for Experiments 2 and 3.

Relative log-likelihood values of the fit self-consistent observer model for every subject (as well as the combined subject Sc). Relative scale is defined as described for Figure 4—figure supplement 1. The self-consistent observer model is consistently outperforming the independent Bayesian model in explaining data from Experiment 2. For Experiment 3 both models are formally identical; the marginal differences in likelihood are simply because their fit parameter values slightly differ due to the joint fit to data from both Experiments 2 and 3 (subject S1; joint fit to all three experiments). Note, the self-consistent and the independent observer model have exactly the same model parameters. Also, a model that does not include noise in the memory recall of the sensory signal generally does not fit the data as well as the full self-consistent observer model.