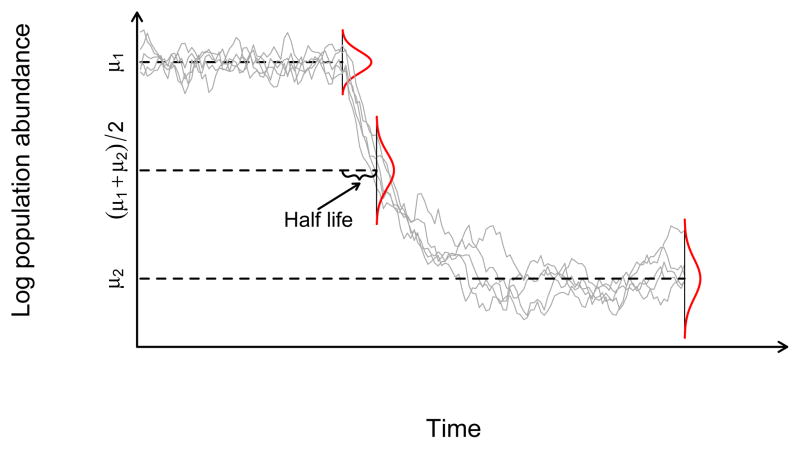
Figure 2.

The stochastic Gompertz change-point process and the half life of the change in the mean of the dynamical process, t̄ = ln(1/2)/ln c₂. Plotted are 5 realizations of the Stochastic Gompertz model of population abundance under a change-point process. Dotted lines mark the process mean before the breakpoint (μ₁), the mean after the breakpoint (μ₂), and the arithmetic average of both means ((μ₁ + μ₂)/2). The time at which such arithmetic average is reached is the half life of the process, t̄. As noted in the text, c₂ = e^−θ₂ corresponds to the post-change point strength of density dependence.