Abstract
Objectives
To investigate the association between recurrent AIDS-defining events and a semi-competing risk of death in patients with advanced, multi-drug resistant HIV infection and to identify individuals at increased risk for these events using a joint frailty model.
Study Design and Setting
368 patients with antiretroviral treatment failure in the OPTIMA Trial randomized to two antiretroviral treatment strategies using a 2x2 factorial design, intensive vs. standard and interruption vs. continuation, and followed for development of AIDS-defining events and death.
Results
Participants were heterogeneous for risk of AIDS-defining events and death (p<0.001) and AIDS-defining events were strongly associated with death (p<0.001), irrespective of treatment. The frailty model was used to classify individuals into high- and low-risk groups based on unobserved heterogeneity. Low-risk individuals were unlikely to die (0%) or have an AIDS-defining event (<4%), while high-risk individuals had event rates approaching 70%. About one-third of high-risk individuals had accelerated mortality, all who died before experiencing an AIDS-defining event. High-risk was associated with being immunocompromised and higher predicted 5-year mortality.
Conclusion
The joint frailty model permits classification of individuals into risk groups based on unobserved heterogeneity that may be identifiable based on observed covariates, providing advantages over the traditional Cox model.
Keywords: Recurring AIDS-defining event, semi-competing risk of death, joint frailty model, frailty risk stratification, OPTIMA Trial
1. Introduction
Over 37 million people are currently infected with the human immunodeficiency virus (HIV) world-wide and over two million were newly HIV infected in 2015 [1]. As a result of HIV infection, many people have developed the acquired immunodeficiency syndrome (AIDS), which is manifested by the development of one or more opportunistic infections or malignancies (AIDS-defining events) as a result of HIV-associated immune system destruction [2]. Although antiretroviral therapy has resulted in a significant decline in AIDS-defining events world-wide, there were over one million AIDS-related deaths in 2015 [1]. Thus, AIDS-defining events are still currently seen in clinical practice, either because of late stage diagnosis, failure of or lack of antiretroviral treatment, or progression of HIV infection.
Recurrent events, such as AIDS-defining events, are common in clinical research as patients may experience more than one event during follow-up [3–6]. These recurrent events can adversely affect a patient’s health and potentially result in death, a semi-competing risk that precludes the event of interest from being observed [7,8]. Thus, recurrent events and death can be dependent and standard survival analysis approaches, such as Cox regression models, are not sufficient because they ignore all subsequent events and only account for the time-to-first-event. These models also assume that a semi-competing risk of death is independent of the event of interest, thus, is censored in the same manner as loss to follow-up. Therefore, in these circumstances the standard models could potentially result in biased parameter estimates, leading to erroneous inferences [4,9–11]. Hence, frailty models are frequently used to analyze recurrent event processes [5,12,13] and are extensions to the standard Cox model.
Frailty models assume that some patients are either more or less likely to experience the events of interest compared to others, i.e., more frail. Frailty captures the “vulnerability” of an individual patient for events and accounts for the unobserved heterogeneity that cannot be explained by observed covariates alone. It can also be viewed as a latent variable that reflects the “health status” of a patient, i.e., some patients may be more vulnerable for an event than others based on unobserved health factors such as genetics, chronic diseases, or lifestyle. These more vulnerable or “frail” patients will a have higher risk of events resulting in heterogeneity among patients leading to a correlation between the subsequent events within a particular subject.
In this article, we present a secondary analysis of the Options in Management of Antiretrovirals (OPTIMA) trial focusing on recurrent AIDS-defining events in the presence of a semi-competing risk of death. OPTIMA, at the time it was conducted, was the largest and longest randomized clinical trial of alternative treatment strategies for patients with advanced, multi-drug resistant HIV infection [14] manifested by the development of one or more opportunistic infections or malignancies and was not CD4 count-based. The primary objective of this clinical trial was to evaluate two treatment strategies in a 2x2 factorial design: 1) intensive vs. standard antiretroviral treatment and 2) interruption vs. continuation of treatment in patients who experienced antiretroviral treatment failure requiring retreatment. The primary analysis assessed the effect of treatment on time-to-first AIDS-defining event, death, and the composite outcome of time to AIDS-defining event or death via the Cox model assuming independent censoring because of death. Although participants in this study experienced more than one AIDS-defining event in the presence of a semi-competing risk of death, this information was not previously analyzed. Therefore, we investigated the impact of antiretroviral treatment on recurrent AIDS-defining events and death using a joint frailty model that simultaneously models the recurrent event and death processes.
2. Methods
2.1. OPTIMA Design
OPTIMA was designed as a 2x2 factorial clinical trial to compare standard antiretroviral treatment (≤ 4 antiretroviral drugs) with intensive ART (5+ antiretroviral drugs) and a 12-week antiretroviral drug-free period interruption vs. no interruption (continuation of treatment). Between 2001 and 2006, 368 individuals with advanced multi-drug resistant HIV infection were enrolled from over 70 clinical sites in three participating countries (United States, Canada, and United Kingdom) and were followed in clinic for a median of 4 years until study closure in 2007. 288 participants were enrolled in the United States, 41 in Canada and 39 in the United Kingdom. Eligible patients had CD4 counts below 300/μl and failed two different multi-drug antiretroviral regimens. Details of the study protocol, procedures and entry characteristics of the study population are reported elsewhere [14–16]. OPTIMA was registered on Clinicaltrials.gov: NCT00050089.
2.2. Outcomes
The outcomes evaluated were death from any cause and AIDS-defining events. An AIDS-defining event has previously been defined by the Centers for Disease Control and Prevention [17]. In this analysis, all types of AIDS-defining events were assumed to be of equal clinical importance, thus, no weighting of AIDS-defining events by severity was done.
2.3. Analysis
Because there was no interaction between treatment and outcome in the primary study results, only the marginal effects of each antiretroviral treatment strategy were analyzed in the 2x2 factorial design, that is, standard vs. intensive and interruption vs. continuation. We did not adjust for baseline covariates in either the Cox or joint frailty models because the randomization produced reasonable balance on baseline characteristics between treatment arms [12]. OPTIMA was powered to detect treatment effects for time to first AIDS-defining event or death [15], but not for the secondary analyses presented herein.
2.3.1. Standard Cox Regression Model
The Cox proportional hazards model was used to analyze time-to-first AIDS-defining event and death, separately. The findings in the original study publication were replicated in this report [14]. For the analysis of AIDS-defining events, patients without an event who were lost to follow-up were censored at their date last seen, i.e., date of death, date lost to follow or date of study completion (administrative censoring). Deaths were considered as independent censoring. For the analysis of death, survivors were censored at their date last seen, i.e., date lost to follow-up or date of study completion. Cox analyses were performed using the PHREG procedure in SAS version 9.4 (SAS Institute Inc.).
2.3.2. Joint Frailty Model
The joint frailty model simultaneously models the recurrent event and death processes linked by a shared common random effect [5,12,13]. Briefly, the hazard (intensity) functions at time t for the recurrent events and death processes can be expressed as
| (1) |
| (2) |
where i indexes patient and j the recurrent event, Zi is a vector of patient level covariates (assumed to be same for both processes in this report), β and α are the respective vectors of regression coefficients for the recurrent events and death processes, vi is the common shared random effect, and g estimates the degree of dependence (association) between the recurrent events and death processes; r0(t) and λ0(t) represent the underlying hazards for recurrent events (1) and death (2), respectively. We assume the random effect vi follows a normal distribution with mean 0 and variance j. In this case, frailty is defined as exp(vi) and has a lognormal distribution [10].
The unobservable random effect vi acts multiplicatively on the hazard functions [i.e., through exp(vi)], so a large value of the random effect will increase the risk of recurrent event and death. The variance of the random effect (j) captures the degree of unobserved heterogeneity among patients [18]. The larger the variance, the more heterogeneity there is among patients with respect to their risk of events, while a null variance indicates patients are homogeneous for their risk of recurrent events.
The g coefficient in equation (2) links the recurrent events and death processes, the larger the value the greater the degree of dependence. When g = 0 the two different survival processes are independent, which is the assumption of the traditional Cox survival model. When g = 1 frailty has the same effect on the recurrent events and death processes, and when g is negative the two processes are negatively correlated. Note, g only has interpretation in the presence of significant heterogeneity or when j is different from zero. Joint frailty models were fitted using the NLMIXED procedure in SAS version 9.4 (SAS Institute Inc.). For all analyses, statistical significance is established at 0.05.
3. Results
3.1. Characteristics of the OPTIMA Cohort
In OPTIMA, 368 patients were randomized to treatment strategy 1 (standard = 192 vs. intensive = 176) and 339 to treatment strategy 2 ( interruption = 164 vs. continuation = 175); 29 patients in the United Kingdom opted out of strategy 2 and were only randomized to strategy 1. The entry characteristics of patients in the two treatment strategies were comparable (Table 1). Nearly all enrolled patients were male (98%), approximately 50% were white, 40% black, and the majority had AIDS or prior AIDS at entry. The Veterans Aging Cohort Study Index (range 0 to 164), a validated predictor of 5-year mortality in those under treatment for HIV infection, was also comparable between treatment groups [19,20]. The Veterans Aging Cohort Study Index includes age, routinely monitored indicators of HIV disease (CD4 count and HIV-1 RNA), and general indicators of organ system injury including hemoglobin, platelets, aspartate and alanine transaminase, creatinine, and viral hepatitis C infection. Higher Veterans Aging Cohort Study Index scores are associated with increased risk of mortality.
Table 1.
Entry characteristics of OPTIMA cohort by treatment strategy*
| Characteristic | Strategy 1 (N=368) | Strategy 2 (N=339) | ||
|---|---|---|---|---|
| Standard N (%) | Intensive N (%) | Interruption N (%) | Continuation N (%) | |
| No. randomized | 192 | 176 | 164 | 175 |
| Age (years) - mean (SD) | 48 (9) | 48 (8) | 49 (8) | 49 (8) |
| Male | 189 (98) | 172 (98) | 160 (98) | 172 (98) |
| White | 90 (47) | 90 (51) | 73 (45) | 87 (50) |
| Black | 80 (42) | 64 (36) | 67 (41) | 71 (41) |
| AIDS or prior AIDS at entry | 107 (56) | 109 (62) | 95 (58) | 105 (60) |
| Hepatitis B virus infection | 26 (14) | 13 (7) | 23 (14) | 14 (8) |
| Hepatitis C virus infection | 46 (24) | 34 (19) | 39 (24) | 38 (22) |
| HIV RNA copies/ml -mean log10 (SD) | 4.7 (0.6) | 4.7 (0.8) | 4.7 (0.7) | 4.8 (0.7) |
| CD4 cells/ul – mean (SD) | 129 (107) | 125 (106) | 129 (106) | 131 (109) |
| Veterans Aging Cohort Study Index | 34.2 (15.6) | 35.0 (15.4) | 34.6 (15.6) | 35.2 (15.3) |
29 United Kingdom patients opted to be randomized to the standard or intensive antiretroviral treatment strategy only
SD = standard deviation
The distribution of AIDS-defining events and deaths by treatment arm within each treatment strategy is displayed in Table 2. During a median follow-up of 4 years, approximately 35% of patients died on each treatment strategy and 35% experienced at least one AIDS-defining event – about 20% had only one AIDS-defining event and 15% had two or more (recurrent) AIDS-defining events. The number of AIDS-defining events was comparable for standard and intensive antiretroviral treatment (107 vs. 106); however, it was somewhat higher for antiretroviral continuation vs. interruption (119 vs. 86). The mean time to first AIDS-defining event and mean time between recurrent AIDS-defining events (gap time) were longer for standard antiretroviral treatment and continuation of antiretroviral treatment.
Table 2.
Number of AIDS defining events and deaths by treatment strategy*
| Outcome | Strategy 1 (N=368) | Strategy 2 (N=339) | ||
|---|---|---|---|---|
| Standard N (%) | Intensive N (%) | Interruption N (%) | Continuation N (%) | |
| No. randomized | 192 | 176 | 164 | 175 |
| No. AIDS-defining events/patient | ||||
| 0 | 128 (67) | 113 (64) | 110 (67) | 107 (61) |
| 1 | 38 (20) | 37 (21) | 32 (20) | 41 (23) |
| 2+ | 26 (14) | 26 (15) | 22 (13) | 27 (15) |
| No. patients with an event | 64 (33) | 63 (36) | 54 (33) | 68 (39) |
| No. events | 107 | 106 | 86 | 119 |
| No. events/patient | 0.55 | 0.60 | 0.52 | 0.68 |
| Mean (SD) time in days between events | 560 (323) | 499 (313) | 464 (313) | 591 (313) |
| Mean (SD) time in days to first event | 647 (551) | 551 (449) | 527 (496) | 673 (508) |
| No. dead | 67 (35) | 61 (35) | 61 (37) | 62 (35) |
| Mean (SD) time in days to death | 877 (543) | 811 (500) | 751 (487) | 967 (538) |
29 United Kingdom patients opted to be randomized to the standard or intensive antiretroviral treatment strategy only
Table 3 displays the association between the number of AIDS-defining events and death for each treatment arm within each treatment strategy. For both treatment strategies, the percent dead increased according to the number of AIDS-defining events per patient, irrespective of treatment. Patients with recurrent AIDS-defining events had nearly three times the risk of dying as those without an event, and those with one AIDS-defining event had approximately double the risk of dying as those without an event. Thus, there is evidence of an association (dependence) between the AIDS-defining event and death processes.
Table 3.
Association between number of AIDS-defining events and death by treatment strategy*
| Number of AIDS-defining events/patient | Strategy 1 (N=368) | Strategy 2 (N=339) | ||
|---|---|---|---|---|
| Standard dead/N (%) | Intensive dead/N (%) | Interruption dead/N (%) | Continuation dead/N (%) | |
| 0 | 29/128 (23) | 28/113 (25) | 26/110 (24) | 28/107 (26) |
| 1 | 19/38 (50) | 16/37 (43) | 19/32 (59) | 16/41 (39) |
| 2+ | 19/26 (73) | 17/26 (65) | 16/22 (73) | 18/27 (67) |
| Total | 67/192 (35) | 61/176 (35) | 61/164 (37) | 62/175 (35) |
29 United Kingdom patients opted to be randomized to the standard or intensive antiretroviral treatment strategy only
3.2. Standard Cox Model Results
The Cox proportional hazards model showed no significant effect of either treatment strategy on time to first AIDS-defining event and death (Table 4). However, there was a suggestion that patients receiving antiretroviral treatment interruption had a lower risk of first AIDS-defining event (hazard ratio (HR) = 0.70, p = 0.09) but a higher risk of death (HR = 1.42, p=0.06) compared to those on continuation of antiretroviral treatment.
Table 4.
Cox and joint frailty model results for recurrent AIDS-defining events and death by treatment strategy
| Outcome | Cox Model | Joint Frailty Model | ||
|---|---|---|---|---|
| Strategy 1 | ||||
| Intensive vs. Standard (N=368) | HR (95% CI) | p-value | HR (95% CI) | p-value |
| AIDS-defining event | 1.30 (0.87, 1.94) | 0.21 | 1.10 (0.67, 1.82) | 0.70 |
| Death | 1.13 (0.79, 1.60) | 0.50 | 1.00 (0.54, 1.89) | 0.98 |
| Frailty | Estimate (SE) | |||
| Heterogeneity (j) | NA | 1.64 (0.15) | <0.001 | |
| Association with death (g) | NA | 1.18 (0.18) | <0.001 | |
| Strategy 2 | ||||
| Interruption vs. Continuation (N=339)** | HR (95% CI) | |||
| AIDS-defining event | 0.70 (0.46,1.07) | 0.09 | 0.99 (0.60, 1.66) | 0.99 |
| Death | 1.42 (0.99, 2.05) | 0.06 | 1.11 (0.59, 2.11) | 0.73 |
| Frailty | Estimate (SE) | |||
| Heterogeneity (j) | NA | 1.67 (0.155) | <0.001 | |
| Association with death (g) | NA | 1.18 (0.185) | <0.001 | |
Time to first AIDS-defining event was analyzed by the Cox Model and time to recurrent AIDS-defining event was analyzed by the joint frailty model.
29 United Kingdom patients opted to be randomized to the standard or intensive antiretroviral treatment strategy only
HR = hazard ratio, CI = confidence interval, SE = standard error, NA= not applicable
3.3. Joint Frailty Model Results
Table 4 also presents the results of fitting a joint frailty model for each treatment strategy on the recurrent AIDS-defining events and death processes. Similar to the Cox model, the joint frailty models show no significant effect of either treatment strategy on AIDS-defining events or death, but with hazard ratios near unity. The joint model indicates significant heterogeneity among patients with respect to recurrent AIDS-defining events (p<0.001 for j) and a significant association between AIDS-defining events and death (p<0.001 for g). The latter is also evident in Table 3, i.e., increasing death rate with increasing number of AIDS-defining events. The heterogeneity and association parameter estimates, j and g, were similar for both treatment strategies. The association parameter estimate was not far from unity (1.18) indicating that frailty has about the same effect on death as AIDS-defining events. The distribution of the patient-level random effect estimates, vi, were similar for each treatment arm within each treatment strategy indicating similar levels of frailty (data not shown). We also examined a gamma frailty and the results were similar (data not shown).
3.3.1. Frailty Risk Subgroups
Because frailty acts multiplicatively on the hazard and to gain further insights into the effect of frailty, we arbitrarily classified individuals into high- and low-risk subgroups based on the exponentiated value of the common shared random effect vi: low-risk, values < 1 (decreased risk for events) and high-risk, values ≥ 1 (increased risk for events). Using this method of classification divided the cohort into approximately equal numbers of high- and low-risk individuals. Table 5 presents the association between AIDS-defining events and death by risk group within each treatment strategy. Low-risk individuals had very few numbers of AIDS-defining events and no deaths, while high-risk individuals had a high percentage of both AIDS-defining events and deaths (approximately 70%). Thus, being high-risk has about the same impact on death as AIDS-defining events and this is reflected in the association parameter (g) with value just above one (1.18).
Table 5.
Association between AIDS-defining events and death by risk group and treatment strategy*
| Number of AIDS-defining events/patient | Low-risk dead/N (%) | High-risk dead/N (%) | Total dead/N (%) |
|---|---|---|---|
| Strategy 1 | |||
| 0 | 0/184 (0) | 57/57 (100) | 57/241 (24) |
| 1 | 0/1 (0) | 35/74 (47) | 35/75 (47) |
| 2+ | 36/52 (69) | 36/52 (69) | |
| Total | 0/185 (0) | 128/183 (70) | 128/368 (35) |
| Strategy 2** | |||
| 0 | 0/163 (0) | 54/54 (100) | 54/217 (25) |
| 1 | 0/7 (0) | 35/66 (53) | 35/73 (48) |
| 2+ | 34/49 (69) | 34/49 (69) | |
| Total | 0/170 (0) | 123/169 (73) | 123/339 (36) |
Strategy 1 = intensive vs. standard antiretroviral treatment; Strategy 2 = antiretroviral treatment interruption vs. continuation
29 United Kingdom patients opted to be randomized to the standard or intensive antiretroviral strategy only
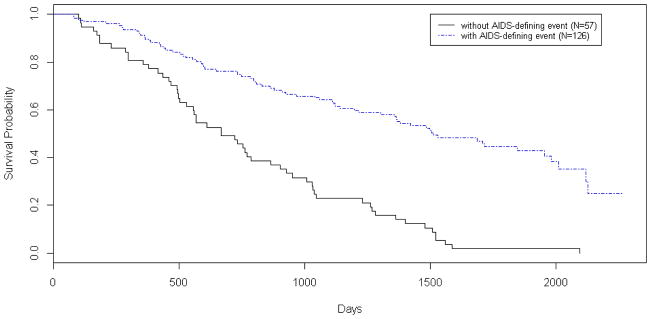
Table 5 also identifies a small group of high-risk individuals who all died before experiencing an AIDS-defining event regardless of treatment strategy. The majority (60%) of whom died from non-HIV related causes. In contrast, the majority of high-risk individuals who died after experiencing an AIDS-defining event died from HIV-related causes (65%). Figure 1 plots Kaplan-Meier survival rates in high-risk individuals with (N = 126) and without AIDS-defining events (N = 57) for strategy 1 (results were similar for strategy 2 and are not shown). Survival was significantly lower in the latter group (logrank p-value <0.001), reflecting a small group of individuals with rapid mortality.
Figure 1.
Cumulative survival rates for high-risk individuals with (blue) and without (black) AIDS-defining events for strategy 1 (logrank p-value <0.001)
Although frailty captures unobserved heterogeneity that cannot be explained by observed covariates alone, we examined the baseline characteristics of high- and low-risk individuals in an attempt to characterize them phenotypically. Given that the treatments did not really work, it allowed us to rely on the principles of randomization to look at these differences. Results for strategy 1 are presented and were similar for strategy 2. Those classified as high-risk tended to be more immunocompromised manifested by lower CD4 counts and higher viral load compared with individuals classified as low-risk. Mean CD4 counts were about 40% lower and under 100/μl in high-risk individuals and viral load was approximately 10% higher compared with low-risk individuals (data not shown). High-risk individuals also had a 36% higher Veterans Aging Cohort Study Index vs. those who were low-risk (39.9 ± 15.4 vs. 29.3 ± 13.6, p < 0.0001), indicative of increased risk for mortality at study entry. Among high-risk individuals, the Veterans Aging Cohort Study Index was about 4 points higher in those without an AIDS-defining event compared to those with an event (42.4 ± 16.4 vs. 38.8 ± 14.9, p = 0.14), which could partly explain their higher mortality. Otherwise, there were no distinguishing observable features between these two risk subgroups.
4. Discussion
The primary analysis of the OPTIMA trial evaluated time to first AIDS-defining event or death via separate Cox models assuming independent censoring. The findings replicated herein showed no significant benefit of either treatment strategy on these two separate clinical outcomes [14]. Because participants could have multiple AIDS-defining events and death could be informative, we reanalyzed the OPTIMA data via a joint frailty model treating death as a competing risk. This model is advantageous because it uses more information than traditional survival models, providing the opportunity to glean further insights into the data.
We found that the joint frailty model was generally consistent with the Cox model results regarding the significance of the effect of each treatment strategy on AIDS-defining events and death, although the hazard ratios were noticeably shrunk towards the null, particularly for strategy 2. A reason for this finding is that AIDS-defining events and death are strongly related and need to be modeled jointly to account for this dependence to avoid biased parameter estimates. Hence, the joint frailty model captures the dependency between the recurrent events and death processes that is not captured by the Cox model. In addition, the joint frailty model showed that patients were heterogeneous (variable) with respect to their risk of AIDS-defining events and death, with similar levels of risk across treatment arms and strategies.
The joint frailty model also afforded the opportunity to retrospectively classify patients into risk subgroups based on the shared random effect, a concept similar to latent class trajectory models [21, 22]. Using this concept, we found that patients who were classified as low-risk were unlikely to die or to have an AIDS-defining event, while high-risk individuals had a high rate of AIDS-defining events and death with similar risk for both events. The model also revealed a small group of high-risk individuals who had a rapid and 100% fatality rate without experiencing any prior AIDS-defining event. These insights into the data provide an advantage of the joint frailty model over the Cox model for the analysis of recurrent events in the presence of dependent censoring. It is important to note that the risk subgroups were determined post hoc based on the results of a model-dependent analysis. Thus, it would not be appropriate to reanalyze the data stratified by risk group.
Although frailty models are designed to account for unobserved heterogeneity that cannot be explained by observed covariates alone, the model can be used in an exploratory way to retrospectively characterize individuals who are at increased risk for outcomes based on the observed data, i.e., a phenotypic classification. Using this strategy, individuals in OPTIMA who were classified as high-risk tended to be more immunocompromised with lower CD4 counts and higher viral load at baseline than those who were classified as low-risk. They also had a higher Veterans Aging Cohort Study Index, indicative of their higher mortality at the time of study entry. The higher Veterans Aging Cohort Study Index has implications for the design of future treatment studies in patients with advanced, multi-drug resistant HIV infection with mortality and AIDS-defining events as outcomes. The index could be used to identify patients at higher risk for these events, lowering overall sample size requirements making the trials more efficient.
A limitation of this study is that different types of AIDS-defining events (e.g. esophageal candidiasis, Pneumocystis jirovecii pneumonia, cytomegalovirus disease, HIV wasting syndrome, etc.) were lumped together and considered to be of similar risk and severity to the patient. Although this assumption simplifies the analyses, it does not take into account the potentially different degrees of clinical impact by each type of event, e.g., some AIDS-defining events can negatively affect a patient’s health more than others. Some approaches have been developed to address this issue within the joint frailty model. For example, Oakes [23] and Xue and Brookmeyer [24] have developed a bivariate frailty model to analyze two types of recurrent events, such as hospitalization and community stays (duration of time outside of hospital), that might be correlated; however, the semi-competing risk of death was not accounted for in the model. Chen and Cook [25] later developed a model that accounts for multiple types of skeletal complications and a dependent terminal event, but the correlation between different types of recurrent events was not considered. Thus, to our knowledge there are no survival models that can account for both different types of recurrent events (clustered within individuals) and a semi-competing risk of death.
Another limitation is that only patient-level analyses were conducted, i.e., recurrent events nested within a patient and termed Level-1 analyses in the literature. In OPTIMA, the randomization was stratified by country and by clinical site within country. Thus, patients could differ within and across countries with respect to case mix, delivery of care, etc., introducing another level of heterogeneity. This additional level of heterogeneity (Level-2) was not taken into account via stratification or covariate adjustment because of the large number of clinical sites (> 70) relative to the few number of individuals enrolled in the trial (N=368). Thus, all clinical sites were considered comparable in the analysis, implying that unobserved factors such as delivery of care, hospital environment, etc. were similar within and between countries. However, there are no analytic methods that could evaluate these components (e.g., recurrent events, semi-competing risk, and multilevel clustering) simultaneously in a joint model.
It is also important to note that OPTIMA represents a unique HIV population of individuals with multi-drug resistant virus and limited retreatment options following multiple antiretroviral treatment regimen failures and with a high risk of mortality; thus, the findings may not be applicable to other HIV populations and might require replication.
In summary, the joint frailty model allows for the dependence between recurrent events and a terminal event, and the estimate of the random effect can be used to classify individuals with different levels of risk for the events. Although frailty models are traditionally used to account for unobserved heterogeneity that cannot be explained by observed covariates alone, the frailty parameter can be used to retrospectively classify individuals into risk groups based on observed characteristics in an exploratory type of analysis, conceptually similar to the approach of latent class trajectory models. This characterization can aid in the design of more efficient clinical trials by identifying a more vulnerable population at high-risk for adverse outcomes, thereby reducing sample size requirements. These features provide an advantage over the traditional Cox analysis.
What is new?
The joint frailty model accounts for unobserved heterogeneity allowing the classification of individuals into groups with different levels of risk that may be identifiable based on observed patient characteristics, conceptually similar to latent class trajectory models. The identification of such patients could aid in the design of future clinical trials by identifying a more vulnerable population at high-risk for adverse outcomes, thereby reducing sample size requirements.
Application of the joint frailty model to the OPTIMA study showed that death and AIDS-defining events were dependent. The model identified a group of high-risk individuals who were at increased risk for both events, including a small subset with accelerated mortality who all died without experiencing an AIDS-defining event. High-risk was also associated with being immunocompromised and having a higher Veterans Aging Cohort Study Index, a validated predictor of mortality for those undergoing treatment for HIV infection. These insights into the data could not be gleaned from a traditional Cox analysis.
Acknowledgments
This work was funded by the Cooperative Studies Program of the Department of Veterans Affairs Office of Research and Development and in part by CTSA Grant Number UL1 TR000142 from the National Center for Advancing Translational Science (NCATS), a component of the National Institutes of Health (NIH). Its contents are solely the responsibility of the authors and do not necessarily represent the official view of NIH and Department of Veterans Affairs. The funders did not have any involvement in the conduct of the research or in the preparation of the article. The VA Cooperative Studies Program approved the submission of the article.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.UNAIDS. AIDS by the Numbers. Geneva, Switzerland: 2016. [Google Scholar]
- 2.Guidelines for the Prevention and Treatment of Opportunistic Infections in HIV-Infected Adults and Adolescents. The National Institutes of Health, and the HIV Medicine Association of the Infectious Diseases Society of America; 2016. [Google Scholar]
- 3.Rogers JK, Pocock SJ, McMurray JJV, Granger CB, Michelson EL, Ostergren J, et al. Analysing recurrent hospitalizations in heart failure: a review of statistical methodology, with application to CHARM-Preserved. Eur J Heart Fail. 2014;16(1):33–40. doi: 10.1002/ejhf.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Amorim LD, Cai J. Modelling recurrent events: a tutorial for analysis in epidemiology. Int J Epidemiol. 2015;44(1):324–33. doi: 10.1093/ije/dyu222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cook RJ. The design and analysis of randomized trials with recurrent events. Stat Med. 1995;14(19):2081–98. doi: 10.1002/sim.4780141903. [DOI] [PubMed] [Google Scholar]
- 6.Kelly PJ, Lim LLY. Survival analysis for recurrent event data: An application to childhood infectious diseases. Stat Med. 2000;19(1):13–33. doi: 10.1002/(sici)1097-0258(20000115)19:1<13::aid-sim279>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 7.Berry SD, Ngo L, Samelson EJ, Kiel DP. Competing risk of death: an important consideration in studies of older adults. J Am Geriatr Soc. 2010;58(4):783–7. doi: 10.1111/j.1532-5415.2010.02767.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Haneuse S, Lee KH. Semi-Competing Risks Data Analysis: Accounting for Death as a Competing Risk When the Outcome of Interest Is Nonterminal. Circ Cardiovasc Qual Outcomes. 2016;9(3):322–31. doi: 10.1161/CIRCOUTCOMES.115.001841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu L, Wolfe RA, Huang X. Shared frailty models for recurrent events and a terminal event. Biometrics. 2004;60(3):747–56. doi: 10.1111/j.0006-341X.2004.00225.x. [DOI] [PubMed] [Google Scholar]
- 10.Rondeau V, Mathoulin-Pelissier S, Jacqmin-Gadda H, Brouste V, Soubeyran P. Joint frailty models for recurring events and death using maximum penalized likelihood estimation: application on cancer events. Biostatistics. 8(4):708–21. doi: 10.1093/biostatistics/kxl043. 200. [DOI] [PubMed] [Google Scholar]
- 11.Belot A, Rondeau V, Remontet L, Georgi R. A joint frailty model to estimate the recurrence process and the disease-specific mortality process without needing the cause of death. Stat Med. 2014;33(18):3147–66. doi: 10.1002/sim.6140. [DOI] [PubMed] [Google Scholar]
- 12.Cai J, Schaubel DE. Handbook of Statistics. Vol. 23. Elsevier; 2003. Analysis of Recurrent Event Data. [Google Scholar]
- 13.Cook JR, Lawless JF. The Statistical Analysis of Recurrent Events. In: Gail M, et al., editors. Statistics for Biology and Health. Springer; 2007. [Google Scholar]
- 14.Holodniy M, Brown ST, Cameron DW, Kyriakides TC, Angus B, Babiker A, et al. Results of antiretroviral treatment interruption and intensification in advanced multi-drug resistant HIV infection from the OPTIMA trial. PLoS One. 2011;6(3):e14764. doi: 10.1371/journal.pone.0014764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kyriakides TC, Babiker A, Singer J, Cameron W, Schechter MT, Holodniy M, Brown ST, Youle M. An open-label randomized clinical trial of novel therapeutic strategies for HIV-infected patients in whom antiretroviral therapy has failed: rationale and design of the OPTIMA Trial. Control Clin Trials. 2003;24(4):481–500. doi: 10.1016/s0197-2456(03)00029-1. [DOI] [PubMed] [Google Scholar]
- 16.Kyriakides TC, Babiker A, Singer J, Piaseczny M, Russo J. Study conduct, monitoring and data management in a trinational trial: the OPTIMA model. Clin Trials. 2004;1(3):277–81. doi: 10.1191/1740774504cn022oa. [DOI] [PubMed] [Google Scholar]
- 17.Castro KG, Ward JW, Slutsker L, Buehler JW, Jaffe HW, Berkelman RL. 1993 revised classification-system for HIV-infection and expanded surveillance case-definition for AIDS among adolescents and adults (Reprinted from Mmwr, Vol 41, Pg Rr 17, 1992) Clin Infect Dis. 1993;17(4):802–10. [PubMed] [Google Scholar]
- 18.Therneau TM, Grambsch PM. Statistics for Biology and Health. Springer; 2001. Modeling Survival Data: Extending the Cox Model. [Google Scholar]
- 19.Justice AC, Modur SP, Tate JP, Althoff KN, Jacobson LP, Gebo KA, et al. Predictive accuracy of the Veterans Aging Cohort Study Index for mortality with HIV infection; A North American Cross Cohort Analysis. J Acquir Immune Defic Syndr. 2013;62:149–63. doi: 10.1097/QAI.0b013e31827df36c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tate JP, Justice AC, Hughes MD, Bonnet F, Reiss P, Mocroft A, et al. An internationally generalizable risk index after one year of antiretroviral therapy. AIDS. 2013;27:563–72. doi: 10.1097/QAD.0b013e32835b8c7f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lin HQ, McCulloch CE, Turnbull BW, Slate EH, Clark LC. A latent class mixed model for analysing biomarker trajectories with irregularly scheduled observations. Stat Med. 2000;19(10):1303–18. doi: 10.1002/(sici)1097-0258(20000530)19:10<1303::aid-sim424>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 22.Lin HQ, Turnbull BW, McCulloch CE, Slate EH. Latent class models for joint analysis of longitudinal biomarker and event process data: Application to longitudinal prostate-specific antigen readings and prostate cancer. J Am Statist Assoc. 2002;97(457):53–65. [Google Scholar]
- 23.Oakes D. Bivariate survival models induced by frailties. J Am Statist Assoc. 1989;84(406):487–93. [Google Scholar]
- 24.Xue X, Brookmeyer R. Bivariate frailty model for the analysis of multivariate survival time. Lifetime Data Anal. 1996;2(3):277–89. doi: 10.1007/BF00128978. [DOI] [PubMed] [Google Scholar]
- 25.Chen BE, Cook RJ. Tests for multivariate recurrent events in the presence of a terminal event. Biostatistics. 2004;5(1):129–43. doi: 10.1093/biostatistics/5.1.129. [DOI] [PubMed] [Google Scholar]