Mixture IRT Model With a Higher-Order Structure for Latent Traits

Abstract

Mixture item response theory (IRT) models have been suggested as an efficient method of detecting the different response patterns derived from latent classes when developing a test. In testing situations, multiple latent traits measured by a battery of tests can exhibit a higher-order structure, and mixtures of latent classes may occur on different orders and influence the item responses of examinees from different classes. This study aims to develop a new class of higher-order mixture IRT models by integrating mixture IRT models and higher-order IRT models to address these practical concerns. The proposed higher-order mixture IRT models can accommodate both linear and nonlinear models for latent traits and incorporate diverse item response functions. The Rasch model was selected as the item response function, metric invariance was assumed in the first simulation study, and multiparameter IRT models without an assumption of metric invariance were used in the second simulation study. The results show that the parameters can be recovered fairly well using WinBUGS with Bayesian estimation. A larger sample size resulted in a better estimate of the model parameters, and a longer test length yielded better individual ability recovery and latent class membership recovery. The linear approach outperformed the nonlinear approach in the estimation of first-order latent traits, whereas the opposite was true for the estimation of the second-order latent trait. Additionally, imposing identical factor loadings between the second- and first-order latent traits by fitting the mixture bifactor model resulted in biased estimates of the first-order latent traits and item parameters. Finally, two empirical analyses are provided as an example to illustrate the applications and implications of the new models.

Multiple latent traits measured by a battery of tests are often correlated and can be assumed to contain a higher-order structure based on substantive knowledge. In certain cases, large-scale measurements, such as the Programme for International Student Assessment (PISA), can be treated as a measurement of three-order latent traits in which multiple domains (e.g., quality, space, and shape; change and relationship; and uncertainty) constitute a subject (mathematics), and three subjects (mathematics, reading, and science) are governed by a general concept of essential knowledge and skill. In this case, the domains, subjects, and general concepts can be treated as the first-, second-, and third-order latent traits, respectively. A general framework of higher-order item response theory (IRT) models has been developed and can accommodate a variety of item response functions for dichotomous and polytomous items (Huang, Wang, Chen, & Su, 2013). Higher-order IRT models have the ability to estimate lower and higher-order latent traits simultaneously and can enhance the testing efficiency using the higher-order latent trait as an indicator of overall assessment for examinees and the lower-order latent traits as an indicator of formative assessment (for an overview, see Huang et al., 2013).

Mixture IRT models (or factor mixture models) have been proposed as a method of accounting for the mixture distributions of different latent classes in latent traits when examinees are classified into the same group according to similar item response patterns rather than according to the observed variables (von Davier & Carstensen, 2010). In major studies, the applications of mixture IRT models focus on measuring a single latent trait and assume that examinee responses from different subgroups follow a specific Rasch model (Rasch, 1960) with different latent trait distributions and different item parameter sets (e.g., Bolt, Cohen, & Wollack, 2001, 2002; Cho & Cohen, 2010; Cohen & Bolt, 2005; Cohen, Gregg, & Deng, 2005; DeMars & Lau, 2011). However, De Boeck, Cho, and Wilson (2011) developed a mixture IRT model under a multidimensional structure to explain the causes of differential item functioning between latent classes, and De Jong and Steenkamp (2010) extended unidimensional mixture IRT models to a multidimensional mixture IRT model for a study on cross-cultural comparisons.

However, potential higher-order relationships among latent traits are rarely discussed in the literature in relation to factor mixture models or mixture IRT models. Because mixtures of latent classes occur in multiple latent traits, the assumption that multiple orders of latent traits may have different mixtures of distributions among latent classes is justified. Thus, a new class of higher-order mixture IRT models is developed in this study. In addition to higher-order IRT models, bifactor models (Gibbons & Hedeker, 1992) were used to measure a common latent trait and several specific latent traits for each test and can be treated as a special case of higher-order IRT models when two orders of latent traits are observed (Yung, Thissen, & McLeod, 1999). This bifactor modeling process is useful in testlets in which the test items in the same testlet are connected by a common stimulus and a specific latent trait for each testlet can model the local dependency among items (Wainer, Bradlow, & Wang, 2007).

Recently, Cho, Cohen, and Kim (2014) developed the mixture bifactor model by accommodating mixtures of latent classes in the bifactor model, and to the best of our knowledge, their study was the first attempt to measure the general and specific domains while simultaneously investigating the effects of different response patterns on both types of dimensionality. Although the mixture bifactor model shares several similarities with our higher-order mixture IRT models in terms of model formulation, the conceptualization differs completely between the two types of models, and the differences should be noted.

First, from a measurement perspective, the latent trait specified for each test or testlet are considered nuisance dimensionality in the mixture bifactor model but measure-intended variables in higher-order mixture IRT models. This differentiation is important because specific latent traits are considered to be a component of test information in higher-order IRT models but should be partially removed from the test information in bifactor models (Huang, Chen, & Wang, 2012).

Second, from a modeling perspective, bifactor models are mathematically equivalent to higher-order IRT models, and the development of higher-order mixture IRT models may appear redundant. Such equivalence between the two models is true when a common latent trait and several specific latent traits are measured; however, if additional common latent traits with additional hierarchical structures are involved, then the current mixture bifactor model is not applicable. In addition, a linear function in the relationship among latent traits in bifactor models is assumed, whereas higher-order IRT models allow for a nonlinear function among second- and first-order latent traits. We will demonstrate the development and application of nonlinear higher-order mixture IRT models in the following sections.

Third, from a model diversity perspective, the item response function can be specified for dichotomous and polytomous items in higher-order IRT models; therefore, its extension to a mixture approach is expected to be more flexible compared with other mixture bifactor models. Fourth, in a general bifactor model for a testlet, the factor loadings (or discrimination parameters) on the specific latent traits can be estimated separately from the factor loadings that are estimated for the common latent trait (Y. Li, Bolt, & Fu, 2006), which allows the effects of general and specific domains on each item to be evaluated. However, the mixture bifactor model of Cho et al. (2014) has imposed an identical loading on both general and specific domains for each item and is therefore considered a restricted mixture bifactor model. We will illustrate the difference in model derivations between the two types of models in detail in the next section.

Finally, the item parameters in the mixture bifactor model were treated as random effects rather than as fixed effects, which cannot be justified as a practical approach in IRT models unless an item population is included (Wang & Wilson, 2005). Based on these previous studies, creating a new class of higher-order mixture IRT models that serves as an extension and supplement to the current mixture bifactor model will be of considerable value. Therefore, this task is the major purpose of the current study and constitutes the most significant contribution of this article to testing practices.

The following sections first introduce mixture IRT models and higher-order IRT models and subsequently elaborate on the development of the new class of higher-order mixture IRT models. Two simulation studies are then conducted to assess the parameter recovery of the developed models and provide a comparison between the developed higher-order mixture IRT models and the mixture bifactor model, and the results are then summarized. Two empirical examples are presented to demonstrate the applications and implications of the new models. The final section provides our conclusions for the new models as well as suggestions for future research.

Mixture IRT Models

Mixture IRT models for dichotomous items combine a dichotomous IRT model (Lord, 1980) and a finite discrete latent class model (McLachlan & Peel, 2000), where a fixed number of discrete latent classes are identified and an IRT model is assumed to underlie the item responses in each latent class. When the item response function follows the three-parameter logistic model (3PLM; Birnbaum, 1968), a mixture 3PLM can be specified, and the probability of a correct response to item i for person n of latent class g can be formulated as

$$P(X_{\mathrm{ngi}}=1|g,{\mathrm{\theta }}_{\mathrm{ng}})={\mathrm{\lambda }}_{\mathrm{gi}}+(1-{\mathrm{\lambda }}_{\mathrm{gi}})\frac{\exp [{\mathrm{\alpha }}_{\mathrm{gi}}({\mathrm{\theta }}_{\mathrm{ng}}-{\mathrm{\delta }}_{\mathrm{gi}})]}{1+\exp [{\mathrm{\alpha }}_{\mathrm{gi}}({\mathrm{\theta }}_{\mathrm{ng}}-{\mathrm{\delta }}_{\mathrm{gi}})]},$$

with

$${\mathrm{\theta }}_{\mathrm{ng}}~N({\mathrm{\mu }}_g,{\mathrm{\sigma }}_g^2),$$

where ${\mathrm{\theta }}_{\mathrm{ng}}$ is the level of the latent trait of person n within class g; ${\mathrm{\lambda }}_{\mathrm{gi}},$${\mathrm{\alpha }}_{\mathrm{gi}},$ and ${\mathrm{\delta }}_{\mathrm{gi}}$ are the pseudo-guessing, discrimination, and difficulty parameters of item i, respectively, for class g; and ${\mathrm{\mu }}_g$ and ${\mathrm{\sigma }}_g^2$ are the mean and variance of the latent trait for class g, respectively. Because the item parameters contain the subscript g for each item, a different set of item parameters can be estimated for different latent classes. When ${\mathrm{\lambda }}_{\mathrm{gi}}=0$ for all items and classes, the mixture two-parameter logistic model (2PLM) can be formulated, and when ${\mathrm{\lambda }}_{\mathrm{gi}}=0$ and ${\mathrm{\alpha }}_{\mathrm{gi}}=1$ for all items and classes, the mixture Rasch model can be formulated (Rost, 1990, 1997).

Although mixture IRT models are flexible and can accommodate a great diversity of item response functions, the mixture Rasch model has been widely applied to latent class detection (e.g., Cho & Cohen, 2010; Cohen & Bolt, 2005; De Boeck et al., 2011; DeMars & Lau, 2011; Frick, Strobl, & Zeileis, 2015) and presents better measurement characteristics than other multiparameter IRT models (Embretson & Reise, 2000). Therefore, we expended considerable efforts to assess the higher-order mixture Rasch model in terms of its estimation efficiency in the following simulation study. In addition to the Rasch model, the higher-order mixture 2PLM and 3PLM were evaluated via simulations and compared with the corresponding mixture bifactor models.

Higher-Order IRT Models

Assume that there are p+ 1 orders on a set of latent traits, where ${\theta }_{\mathrm{nv}}^{(p)}$ is the pth-order vth latent trait for person n and ${\mathbf{\theta }}_n^{(p+1)}$ is a vector of p+ 1th-order latent traits for person n. The relationship between the pth- and p+ 1th-order latent traits can be expressed as

$${\mathrm{\theta }}_{\mathrm{nv}}^{(p)}={\mathbf{\beta }}^{(p)}{\mathbf{\theta }}_n^{(p+1)}+{\mathrm{\epsilon }}_{\mathrm{nv}}^{(p)},$$

where ${\mathbf{\beta }}^{(p)}$ is a vector of regression parameters (factor loadings) and ${\epsilon }_{\mathrm{nv}}^{(p)}$ represents the residuals for person n and test v and is assumed to be normally distributed (with a mean of zero) and independent of other $\mathrm{\theta }$ variables. Variations of Equation 3 can be attained if higher-order latent traits have polynomial and interaction effects on low-order latent traits. In the following section, the polynomial or nonlinear formulation will be illustrated.

Assuming a two-order structure with one common second-order latent trait and several first-order latent traits, for simplicity, the probability of a correct response to item i in test v for person n in the higher-order 3PLM is

$$P(X_{\mathrm{niv}}=1|{\mathrm{\theta }}_{\mathrm{nv}}^{(1)})={\mathrm{\lambda }}_{\mathrm{iv}}+(1-{\mathrm{\lambda }}_{\mathrm{iv}})\frac{\exp [{\mathrm{\alpha }}_{\mathrm{iv}}({\mathrm{\theta }}_{\mathrm{nv}}^{(1)}-{\mathrm{\delta }}_{\mathrm{iv}})]}{1+\exp [{\mathrm{\alpha }}_{\mathrm{iv}}({\mathrm{\theta }}_{\mathrm{nv}}^{(1)}-{\mathrm{\delta }}_{\mathrm{iv}})]},$$

with

$${\mathrm{\theta }}_{\mathrm{nv}}^{(1)}={\mathrm{\beta }}_v{\mathrm{\theta }}_n^{(2)}+{\mathrm{\epsilon }}_{\mathrm{nv}}^{(1)},$$

where λ_iv, α_iv, and δ_iv are the pseudo-guessing, discrimination, and difficulty parameters for item i of test v, respectively; ${\theta }_n^{(2)}$ and ${\theta }_{\mathrm{nv}}^{(1)}$ are the second-order and vth first-order latent traits for person n, respectively; ${\mathrm{\beta }}_v$ is the factor loading of ${\theta }_n^{(2)}$ on ${\theta }_{\mathrm{nv}}^{(1)};$${\epsilon }_{\mathrm{nv}}^{(1)}$ is the residual; and the other parameters are as previously defined. Similarly, the higher-order 2PLM and the higher-order Rasch model can be formulated when ${\mathrm{\lambda }}_{\mathrm{iv}}=0$ and both ${\mathrm{\lambda }}_{\mathrm{iv}}=0$ and ${\mathrm{\alpha }}_{\mathrm{iv}}=1$ are constrained, respectively. Other model extensions for higher-order latent traits within the framework of IRT models are referred to in the work of Huang et al. (2013) and Huang and Wang (2013, 2014).

Higher-Order Mixture IRT Models

If manifest groups are either not available or not reliable, a mixture IRT model can be implemented (De Boeck et al., 2011), and the same situations can apply to higher-order IRT models. Let $g_1$ and $g_2$ be the indices of latent classes that arise in the first- and second-order latent traits. Thus, the mixtures of latent classes can be accommodated in the higher-order 3PLM by formulating the probability of correctly answering item i of test v for person n within classes $g_1$ and $g_2$ as follows:

$$P(X_{n{g}_1{g}_2\mathrm{iv}}=1|g_1,g_2,{\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)})={\mathrm{\lambda }}_{g_1{g}_2\mathrm{iv}}+(1-{\mathrm{\lambda }}_{g_1{g}_2\mathrm{iv}})\frac{\exp \left[{\mathrm{\alpha }}_{g_1{g}_2\mathrm{iv}}({\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}-{\mathrm{\delta }}_{g_1{g}_2\mathrm{iv}})\right]}{1+\exp \left[{\mathrm{\alpha }}_{g_1{g}_2\mathrm{iv}}({\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}-{\mathrm{\delta }}_{g_1{g}_2\mathrm{iv}})\right]},$$

with

$${\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}={\mathrm{\beta }}_{g_{1}v}{\mathrm{\theta }}_{n{g}_2}^{(2)}+{\mathrm{\epsilon }}_{n{g}_{1}v}^{(1)},$$

and

$${\mathrm{\theta }}_{n{g}_2}^{(2)}={\mathrm{\eta }}_{g_2}^{(2)}+{\mathrm{\gamma }}_{n{g}_2}^{(2)},$$

where ${\mathrm{\lambda }}_{g_1{g}_2\mathrm{iv}},$${\mathrm{\alpha }}_{g_1{g}_2\mathrm{iv}},$ and ${\mathrm{\delta }}_{g_1{g}_2\mathrm{iv}}$ are the pseudo-guessing, discrimination, and difficulty parameters for item i of test v in classes $g_1$ and $g_2,$ respectively; ${\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}$ is the vth first-order latent traits for person n within classes $g_1$ and $g_2$; ${\mathrm{\theta }}_{n{g}_2}^{(2)}$ is the second-order latent trait for person n of class $g_2;$${\mathrm{\beta }}_{g1v}$ is the factor loading for test v in class $g_1;$${\mathrm{\epsilon }}_{\mathrm{ng}1v}^{(1)}$ is the residual in test v for person n within class $g_1$ and is assumed to be normally distributed; η_g2 is the mean second-order latent trait for class $g_2;$ and ${\mathrm{\gamma }}_{n{g}_2}^{(2)}$ is the second-order latent trait residual for person n of class $g_2$ and is assumed to follow a normal distribution (with a mean of zero) and be independent of other random-effect variables among latent classes.

Higher-order mixture IRT models are very flexible and general such that different orders can have different numbers of latent classes. For example, one may assume two latent classes in the second order and four latent classes in the first order based on substantive theory or empirical findings. For simplicity and ease of interpretation, the same number of latent classes was assumed across orders in this study; therefore, the subscripts g₁ and g₂ were reduced to g. In the following simulation studies, when the Rasch model is used as the item response function, we assumed that all latent classes had an identical set of factor loadings (i.e., metric invariance was assumed, see below). Therefore, ${\mathrm{\beta }}_{g_{1}v}$ was simplified to ${\mathrm{\beta }}_v$ and ${\mathrm{\epsilon }}_{\mathrm{ng}1v}^{(1)}$ was simplified to ${\mathrm{\epsilon }}_{\mathrm{nv}}^{(1)}.$ Furthermore, when the 2PLM and 3PLM were used, different sets of factor loadings were estimated and the assumption of metric invariance was relaxed.

It is worth noting the major differences between the model proposed here and the mixture bifactor model proposed by Cho et al. (2014). In the developed higher-order mixture 3PLM, after combining Equations 6 and 7, the numerator of the probability function in Equation 6 can be expressed as $\exp [{\mathrm{\alpha }}_{g_1{g}_2\mathrm{iv}}({\mathrm{\beta }}_{g_{1}v}{\mathrm{\theta }}_{n{g}_2}^{(2)}+{\mathrm{\epsilon }}_{n{g}_{1}v}^{(1)}-{\mathrm{\delta }}_{g_1{g}_2\mathrm{iv}})].$ Corresponding to the mixture bifactor model (Cho et al., 2014), ${\mathrm{\theta }}_{n{g}_2}^{(2)}$ is the general factor and ${\mathrm{\epsilon }}_{n{g}_{1}v}^{(1)}$ is the specific factor; however, the regression weights of the second-order latent trait on the first-order latent traits (i.e., ${\mathrm{\beta }}_{g1v}$) were not attainable (i.e., fixed to one). Therefore, the general and specific factors share a common set of factor loadings (or discrimination parameters) for each latent class. Such constraints in the mixture bifactor model limit its applicability because the factor loadings are important indicators of the effect that the general and specific factors have on each test item in real testing situations. In addition, the subscripts g₁ and g₂, which indicate the class membership in the first and second orders, respectively, reduce to a single indicator of g because the number of classes is constrained to the same number for the general and specific factors in the mixture bifactor model.

Issues of measurement invariance deserve further attention in higher-order mixture IRT models. When the discrimination parameters ($\mathrm{\alpha }\mathrm{s}$) are fixed to one and the factor loadings ($\mathrm{\beta }\mathrm{s}$) are assumed to be equal across latent classes, a restricted version of higher-order mixture IRT models can be formulated. Such a constraint on identical factor loadings results in an absences of latent class mixtures in the first-order latent traits; therefore, latent classes are present in the second-order latent trait because of the relationship between the factor loadings and first-order residuals (i.e., the variance of ${\mathrm{\epsilon }}_{\mathrm{ng}1v}^{(1)}$ is equal to $1-{\mathrm{\beta }}_{g_{1}v}^2$ when the corresponding second-order latent trait is standardized). If one of these terms lacks a $g_1$ subscript (e.g., ${\mathrm{\beta }}_v$), the other parameter also lacks such a subscript (e.g., ${\mathrm{\epsilon }}_{\mathrm{nv}}^{(1)}$). The imposition of equivalence constraints on the discrimination parameters across items and the factor loadings across classes implies that the assumption of metric invariance is satisfied. However, the assumption of scalar invariance is not fulfilled because the item difficulties are allowed to differ for each latent class (De Boeck et al., 2011; Horn & McArdle, 1992; Millsap & Kwok, 2004; Vandenberg & Lance, 2000). When appropriate, the constraints of equal factor loadings and first-order residual variances or identical discrimination parameters across latent classes and items can be relaxed. Two conditions that can be used to determine whether the metric is invariant will be demonstrated in the following simulation studies.

For identification purposes, the mean second-order latent trait for one class (e.g., the first latent class and g₂ = 1) is set to zero, and its corresponding residual variance is set to one. The mean item difficulty of each test for other classes (g₂ = 2, . . . , G) is set to an identical value as that of the mean item difficulty of the first latent class in each test. A further constraint should be considered when the metric invariance is violated. For the higher-order mixture 2PLM and 3PLM, we set the variances of ${\mathrm{\gamma }}_{n{g}_2}^{(2)}$ and ${\mathrm{\epsilon }}_{\mathrm{ng}1v}^{(1)}$ equal to one and $1-{\mathrm{\beta }}_{g1v}^2,$ respectively, such that the first-order latent traits follow a standard normal distribution and the factor loadings can be interpreted as the correlation between the second- and first-order latent traits. Note that the constraints on the first-order residual (or the specific factor) variances are not necessary in the mixture bifactor model (Cho et al., 2014) because the factor loadings (${\mathrm{\beta }}_{g1v}$) are set to one for all tests and classes. Setting these constraints on model parameters to identify the model is common practice in the literature on mixture IRT models (e.g., De Boeck et al., 2011; De Jong & Steenkamp, 2010; Paek & Cho, 2015; von Davier & Carstensen, 2010).

Nonlinear Higher-Order Mixture IRT Model

The proposed models mentioned above assume a linear relationship between higher- and lower-latent traits. Therefore, in real testing situations, linear factor analysis models may be unrealistic in many applications and yield a poor fit to the data (McDonald, 1962, 1967; Yalcin & Amemiya, 2001). In addition, because the mixtures of distributions in the second-order latent trait are of particular interest in this study and the second-order latent trait is often formulated to include polynomials in a nonlinear factor model, an investigation of the effects of mixtures of latent classes on model parameter estimations in a nonlinear or quadratic higher-order IRT model is justifiable. Therefore, a nonlinear regression curve may be a plausible alternative and can be applied to higher-order mixture IRT models in the form of a polynomial of degree r on the second-order latent trait, where the relationship between the second- and first-order latent traits is given by

$${\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}={\mathbf{\beta }}_{g_{1}v}{\mathbf{\theta }}_{n{g}_2}^{(2)}+{\mathrm{\epsilon }}_{n{g}_{1}v}^{(1)},$$

where ${\mathbf{\beta }}_{g_{1}v}=[{\mathrm{\beta }}_{1g_{1}v},\dots ,{\mathrm{\beta }}_{r{g}_{1}v}]$ is a vector of length r for the regression weights of polynomials for test v in class $g_1,$${\mathbf{\theta }}_{n{g}_2}^{{(2)}^{\prime }}=[{\mathrm{\theta }}_{n{g}_2}^{{(2)}^1},\dots ,{\mathrm{\theta }}_{n{g}_2}^{{(2)}^{\mathrm{r}}}]$ is a vector of polynomials in the second-order latent trait within class $g_2$ (if $r=1,$Equation 9 will collapse into the linear higher-order mixture IRT model as in Equation 7), and the other parameters are as defined above. Consider the quadratic factor model as an example (i.e., $r=2$). To ensure that the polynomials in the second-order latent trait are mutually orthogonal, a different type of parameterization is used to replace Equation 9 with

$${\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}={\mathrm{\beta }}_{g_{1}v1}{\mathrm{\theta }}_{n{g}_2}^{(2)}+{\mathrm{\beta }}_{g_{1}v2}\left(\frac{{\mathrm{\theta }}_{n{g}_2}^{{(2)}^2}-1}{\sqrt{2}}\right)+{\mathrm{\epsilon }}_{n{g}_{1}v}^{(1)}.$$

If $r=3,$ the formulation can be expressed as

$${\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}={\mathrm{\beta }}_{g_{1}v1}{\mathrm{\theta }}_{n{g}_2}^{(2)}+{\mathrm{\beta }}_{g_{1}v2}\left(\frac{{\mathrm{\theta }}_{n{g}_2}^{{(2)}^2}-1}{\sqrt{2}}\right)+{\mathrm{\beta }}_{g_{1}v3}\left(\frac{{\mathrm{\theta }}_{n{g}_2}^{{(2)}^3}-3\times {\mathrm{\theta }}_{n{g}_2}^{(2)}}{\sqrt{6}}\right)+{\mathrm{\epsilon }}_{n{g}_{1}v}^{(1)}.$$

The generalizations of the nonlinear factor models can be found in the references of McDonald’s studies (1962, 1967); these generalizations indicate that a higher complexity of these extensions (e.g., $r>3$) increases the flexibility of the nonlinear higher-order mixture IRT model. Similar to the linear higher-order mixture IRT model, the model identification settings, latent trait and residual distributions, and measurement invariance features can directly apply to the nonlinear higher-order mixture IRT model. Following the constraints in the linear higher-order mixture Rasch model, we assumed that all latent classes shared a set of regression weights; thus, the subscript $g_1$ was omitted from Equations 9 to 11.

Posterior Distribution and Bayesian Estimation

Assume that both orders have the same latent classes ($g_1$ and $g_2$ simplify to g) and let the parameter space in the higher-order mixture Rasch model be denoted as

$$S=\{{\mathrm{\theta }}_{\mathrm{ng}}^{(2)}{,\mathrm{\eta }}_g^{(2)},{\mathrm{\gamma }}_{\mathrm{ng}}^{(2)},{\mathrm{\theta }}_{\mathrm{ngv}}^{(1)},{\mathrm{\beta }}_{\mathrm{gv}},{\mathrm{\epsilon }}_{\mathrm{ngv}}^{(1)},{\mathrm{\lambda }}_{\mathrm{giv}},{\mathrm{\alpha }}_{\mathrm{giv}},{\mathrm{\delta }}_{\mathrm{giv}},{\mathrm{\pi }}_g\},$$

where ${\mathrm{\pi }}_g$ indicates the mixing proportion for class g. The joint posterior distribution of the parameters can then be expressed as

$$\begin{array}{cc}\multicolumn{1}{c}{}& P(S|\mathbf{X})\propto L(g,{\mathrm{\theta }}_{\mathrm{ngv}}^{(1)},{\mathrm{\lambda }}_{\mathrm{giv}},{\mathrm{\alpha }}_{\mathrm{giv}},{\mathrm{\delta }}_{\mathrm{giv}}|\mathbf{X})P({\mathrm{\eta }}_g^{(2)})P({\mathrm{\gamma }}_{\mathrm{ng}}^{(2)})P({\mathrm{\beta }}_{\mathrm{gv}})P({\mathrm{\epsilon }}_{\mathrm{ngv}}^{(1)})P({\mathrm{\lambda }}_{\mathrm{giv}})P({\mathrm{\alpha }}_{\mathrm{giv}})P({\mathrm{\delta }}_{\mathrm{giv}})P({\mathrm{\pi }}_g)\hfill \\ \multicolumn{1}{c}{}& \times P(g|{\mathrm{\pi }}_g)P({\mathrm{\theta }}_{\mathrm{ng}}^{(2)}|{\mathrm{\eta }}_g^{(2)},{\mathrm{\gamma }}_{\mathrm{ng}}^{(2)})P({\mathrm{\theta }}_{\mathrm{ngv}}^{(1)}|{\mathrm{\theta }}_{\mathrm{ng}}^{(2)},{\mathrm{\beta }}_{\mathrm{gv}},{\mathrm{\epsilon }}_{\mathrm{ngv}}^{(1)}),\hfill \end{array}$$

with the likelihood function calculated by

$$L(g,{\mathrm{\theta }}_{\mathrm{ngv}}^{(1)},{\mathrm{\lambda }}_{\mathrm{giv}},{\mathrm{\alpha }}_{\mathrm{giv}},{\mathrm{\delta }}_{\mathrm{giv}}|\mathbf{X})=\underset{n=1}{\overset{N}{\Pi }}\underset{v=1}{\overset{V}{\Pi }}\underset{i=1}{\overset{I}{\Pi }}{\left[\begin{array}{c}\hfill {\{\sum _{g=1}^G{\mathrm{\pi }}_{g}P(X_{\mathrm{niv}}=1|g,{\mathrm{\theta }}_{\mathrm{ngv}}^{(1)},{\mathrm{\lambda }}_{\mathrm{giv}},{\mathrm{\alpha }}_{\mathrm{giv}},{\mathrm{\delta }}_{\mathrm{giv}})\}}^{{\upsilon }_{\mathrm{niv}}}\hfill \\ \multicolumn{1}{c}{\times {\{1-\sum _{g=1}^G{\mathrm{\pi }}_{g}P(X_{\mathrm{niv}}=1|g,{\mathrm{\theta }}_{\mathrm{ngv}}^{(1)},{\mathrm{\lambda }}_{\mathrm{giv}},{\mathrm{\alpha }}_{\mathrm{giv}},{\mathrm{\delta }}_{\mathrm{giv}})\}}^{1-{\upsilon }_{\mathrm{niv}}}}\end{array}\right]}^{{\xi }_{\mathrm{ng}}^l},$$

where υ_niv is dichotomously scored as 1 if person n correctly responds to item i of test v and scored as 0 otherwise; ${\mathrm{\xi }}_{\mathrm{ng}}^l$ is equal to 1 if person n is sampled from latent class g and equal to 0 otherwise at iteration l; and the other parameters are as defined above.

The random-effect variables of $\mathrm{\theta },$$\mathrm{\gamma },$ and $\mathrm{\epsilon }$ increase the difficulty and decrease the efficiency of using the integral of the joint posterior distribution in conventional marginal maximum likelihood estimation because high dimensionality is involved. Thus, Bayesian estimation with Markov chain Monte Carlo (MCMC) methods were implemented to produce the full conditional distributions of the parameters to represent the joint posterior distributions, and the mean of the marginal posterior density was treated as the parameter estimate of interest.

Before applying the Bayesian estimation, a prior distribution for each parameter is required. The same priors were set in the following simulations and empirical analyses. For the item parameters, a normal prior distribution with a mean of 0 and a variance of 4 was used for the difficulty parameters, a lognormal distribution with a mean of 0 and a variance of 1 was used for the discrimination parameters, and a beta prior with both hyperparameters equal to 1 was set for the pseudo-guessing parameters. For the person parameters, a normal prior distribution with a mean of 0 and a variance of 10 was used for the second-order latent trait mean and a normal prior distribution with a mean of 0.5 and a variance of 10 was applied for the regression weights. A gamma prior distribution with both hyperparameters equal to 0.01 was specified for the inverse of the second- and first-order latent trait residual variances. A categorical prior distribution was set for the indicators of latent classes with a conjugate Dirichlet distribution in which the hyperparameters were set to one. The settings of the prior distributions for the model parameters were consistent with the IRT literature using Bayesian estimation to calibrate the parameters (Bolt, Wollack, & Suh, 2012; Cao & Stokes, 2008; Cho & Cohen, 2010; Cho et al., 2014; Cohen & Bolt, 2005; de la Torre & Hong, 2010; de la Torre & Song, 2009; Fox, 2010; Huang et al., 2013; Hung & Wang, 2012; Klein Entink, Fox, & van der Linden, 2009; Y. Li et al., 2006).

Methods

Simulation Design

To assess the efficiency of the proposed models and examine the parameter recovery, the following two simulations were conducted: one for the higher-order mixture Rasch model, which included linear and nonlinear approaches, and the other for the higher-order mixture 2PLM and 3PLM, which were compared with the mixture bifactor model. Each study contained five first-order latent traits (i.e., five tests) and one second-order latent trait, and it was assumed that there were two latent classes: a majority class (60%) and a minority class (40%). For the linear higher-order mixture Rasch model, the two manipulated factors were sample size (1,000 or 2,000 persons) and test length (20 or 30 items in each test). The majority class had a mean of zero, the minority class had a mean of −0.5 for the second-order latent trait (i.e., η_g), and both classes had a variance of 1 for the second-order residual variance (i.e., the variance of γ_ng). The factor loadings were set to 0.9, 0.8, 0.7, 0.6, and 0.5 for the five first-order latent traits, and their residual variances were set to 0.19, 0.36, 0.51, 0.64, and 0.75 (i.e., $1-{\mathrm{\beta }}_v^2$) for the two latent classes, respectively.

For the nonlinear higher-order mixture Rasch model, a quadratic higher-order mixture Rasch model was used to generate simulated data. The sample size (2,000 or 3,000 persons) and test length (20 or 30 items in each test) were varied. A larger sample size was used in the second simulation study because the nonlinear mixture model requires additional subjects to obtain a stable estimation. The ability distributions for the second-order latent trait for both classes were identical to those of the linear approach except that the mean second-order latent trait across classes was constrained to zero. The factor loadings were obtained from an empirical example (Muthén & Muthén, 2012) and set to 1.000, 1.050, 1.119, 0.986, and 1.093 for the five first-order latent traits in the linear factor term (i.e., ${\mathrm{\theta }}_{\mathrm{ng}}^{(2)}$) and −0.253, −0.251, −0.185, −0.203, and −0.210 for the five first-order latent traits in the quadratic factor term (i.e., ${(\mathrm{\theta }}_{\mathrm{ng}}^{(2)}-1)/\sqrt{2}$). The same example was used to obtain residual variances with values of 0.976, 0.944, 0.945, 1.116, and 1.001 for the five first-order latent traits.

In the second simulation study, the higher-order mixture 2PLM and 3PLM were used to generate responses by 2,000 examinees to 20 or 30 items in each test. The settings related to the distributions of the second- and first-order latent traits were set to the same values used in the linear higher-order mixture Rasch model. The majority class had the same factor loadings as the first simulation study of the linear approach, and the minority class had factor loading values of 0.50, 0.60, 0.70, 0.80, and 0.90 for the five first-order latent traits. When the item responses were generated, we used the generating model and its corresponding mixture bifactor model to fit the data and assess the consequences of implementing a misleading constraint of identical factor loadings in the mixture bifactor model.

For both simulations, the item parameters were generated with the distribution described below. Equally spaced values ranging between −2 and 2 were used to generate the item difficulty parameters in steps of $\frac{4}{19}$ for the 20-item test and steps of $\frac{4}{29}$ for the 30-item test for the majority class. A value of 0.5 or −0.5 was uniformly added to the item difficulties for the minority class; thus, the mean item difficulty in the test was set to the same value for both classes. When the 2PLM and 3PLM are used as the item response functions, additional item parameters should be considered. The item discrimination parameters were generated from a uniform distribution between 0.50 and 1.50 for both classes. Each test had a common pseudo-guessing parameter that was generated from a uniform distribution between 0.20 and 0.30 for the majority class and between 0.10 and 0.20 for the minority class because this parameter is too uncertain to estimate precisely and such a constraint is a common practice in real testing situations (van der Linden, Klein Entink, & Fox, 2010). The specifications of the model parameters were consistent with those commonly found in practice. For both studies, 30 replications were conducted under each condition because we found a smaller sampling variation across replications when the number of replications exceeded thirty.

Analysis

Bayesian estimation with MCMC methods was used to calibrate the model parameters using the WinBUGS freeware program (Spiegelhalter, Thomas, & Best, 2003). The priors for the model parameters were set as previously described, and three parallel chains were conducted for five randomly selected simulated data sets under each condition to assess the parameter convergence using the multivariate potential scale reduction factor (Brooks & Gelman, 1998) and monitor whether the phenomenon of label switching occurred. Ordinal constraints were imposed on the mixing proportions to ensure that the majority group had a higher proportion than the minority group to avoid label switching (McLachlan & Peel, 2000). The results indicated that 15,000 iterations were sufficient to reach stationarity for all of the structural parameters, with the first 5,000 iterations defined as the burn-in period because all of the multivariate potential scale reduction factors were close to unity. No label switching was observed because the three chains mixed well and multiple modes were not observed in the marginal posterior densities. The WinBUGS commands for the proposed models are available on request.

For each estimator, the bias and root mean square error (RMSE) were calculated to assess the parameter recovery in the two simulation studies according to Equations 15 and 16:

$$\mathrm{Bias}(\mathrm{EAP}({\mathrm{\zeta }}_r))=\sum _{r=1}^R(\mathrm{EAP}({\mathrm{\zeta }}_r)-\mathrm{\zeta })/R,$$

$$\mathrm{RMSE}(\mathrm{EAP}({\mathrm{\zeta }}_r))=\sqrt{\sum _{r=1}^R{(\mathrm{EAP}({\mathrm{\zeta }}_r)-\mathrm{\zeta })}^2/R},$$

where R is the number of simulation replications, $\mathrm{\zeta }$ is the generated value, and $\mathrm{EAP}({\mathrm{\zeta }}_r)$ is the expected posterior estimate in replication r.

For model comparisons, Bayesian information criterion (BIC; Schwarz, 1978) was used to select the best-fitting model that provided a better explanation of the data compared with Bayesian deviance information criterion (DIC) because the Bayesian DIC index is seldom used in mixture IRT models (Cao & Stokes, 2008; De Jong & Steenkamp, 2010). In addition, the BIC index has been found to be more efficient than other indices across different types of dichotomous mixture IRT models (Cho & Cohen, 2010; Cho et al., 2014; F. Li, Cohen, Kim, & Cho, 2009).

This study included the following expectations: (a) the model parameters could be well recovered for both the linear and nonlinear higher-order mixture Rasch models using MCMC methods; (b) the latent classes that include classifications of individuals could be correctly identified; (c) a longer test and larger sample size enable more precise estimations of the model parameters; and (d) ignoring the differential factor loadings among latent traits by constraining identical factor loadings (i.e., fixed to one) in the mixture bifactor model results in biased items and person parameter estimations.

Results

Simulation Study 1: The Higher-Order Mixture Rasch Model

Because of space constraints, the bias and RMSE values for individual parameters are not reported; instead, their means and standard deviations are provided. Table 1 summarizes the bias and RMSE values for the linear higher-order mixture Rasch model with a sample size of 1,000. The bias values were close to zero across all conditions. For the short test length of 20 items, the mean RMSE was between 0.040 and 0.125 for all estimators in the majority class and between 0.040 and 0.198 for those in the minority class. When the test length was increased to 30 items, the mean RMSE was between 0.030 and 0.122 for all estimators in the majority class and between 0.030 and 0.160 for those in the minority class. The parameter recovery was satisfactory because the RMSE values were acceptably small. In addition, the majority class yielded better parameter recovery than the majority class because of the greater proportion of examinees in the majority class.

Table 1.

Parameter Recovery for the Linear Higher-Order Mixture Rasch Model With a Sample Size of 1,000.

Test length	20				30
Class	Majority		Minority		Majority		Minority
Criterion	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
Parameter
Difficulty
Test 1
Mean	0.015	0.125	0.015	0.176	0.013	0.122	0.013	0.160
SD	0.031	0.017	0.035	0.045	0.023	0.017	0.028	0.031
Test 2
Mean	0.003	0.122	0.003	0.175	0.019	0.115	0.019	0.156
SD	0.029	0.017	0.029	0.028	0.025	0.021	0.030	0.030
Test 3
Mean	0.008	0.119	0.008	0.171	0.010	0.109	0.010	0.151
SD	0.023	0.014	0.035	0.039	0.018	0.017	0.026	0.030
Test 4
Mean	0.015	0.119	0.015	0.169	0.019	0.111	0.019	0.147
SD	0.025	0.022	0.035	0.023	0.027	0.015	0.022	0.023
Test 5
Mean	0.000	0.123	0.000	0.170	0.015	0.109	0.015	0.152
SD	0.028	0.019	0.040	0.028	0.025	0.015	0.023	0.026
Second-order
${\overline{\mathrm{\theta }}}^{(2)}$	—	—	−0.007	0.099	—	—	0.021	0.096
${\mathrm{Var}(\mathrm{\theta }}^{(2)})$	—	—	0.065	0.198	—	—	−0.005	0.111
Loading
β1	0.009	0.053	—	—	0.020	0.040	—	—
β2	−0.017	0.053	—	—	0.016	0.035	—	—
β3	−0.004	0.044	—	—	0.007	0.030	—	—
β4	−0.015	0.040	—	—	0.008	0.034	—	—
β5	0.000	0.044	—	—	0.010	0.039	—	—
Residual
Mean	0.009	0.070	0.012	0.090	0.003	0.055	0.009	0.071
SD	0.016	0.020	0.025	0.018	0.008	0.009	0.011	0.013

Note. RMSE = root mean square error; Second-order = second-order latent trait; Loading = factor loading; Residual = residual variance; — = not applicable because of model constraints.

When the sample size was increased to 2,000 (as shown in Table 2), the bias values were also close to zero and the RMSE values were smaller than those in the small sample size. For the 20-item test length, the mean RMSE ranged from 0.022 to 0.088 for all estimators in the majority class and from 0.022 to 0.117 for those in the minority class, whereas for the 30-item test length, the mean RMSE ranged from 0.023 to 0.083 for all estimators in the majority class and from 0.022 to 0.104 for those in the minority class. The findings for the small sample size were applied to the large sample size. In summary, the parameters were recovered well for both latent classes, the test length had only a slight impact on the parameter estimation, and the large sample size allowed for a better parameter recovery.

Table 2.

Parameter Recovery for the Linear Higher-Order Mixture Rasch Model With a Sample Size of 2,000.

Test length	20				30
Class	Majority		Minority		Majority		Minority
Criterion	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
Parameter
Difficulty
Test 1
Mean	0.007	0.088	0.007	0.120	0.004	0.083	0.004	0.101
SD	0.024	0.013	0.016	0.022	0.015	0.011	0.020	0.015
Test 2
Mean	0.007	0.088	0.007	0.113	−0.002	0.080	−0.002	0.103
SD	0.023	0.014	0.022	0.024	0.019	0.014	0.024	0.025
Test 3
Mean	0.006	0.081	0.006	0.117	0.002	0.080	0.002	0.100
SD	0.016	0.013	0.020	0.023	0.013	0.011	0.019	0.015
Test 4
Mean	−0.001	0.086	−0.001	0.115	0.005	0.082	0.005	0.104
SD	0.023	0.015	0.020	0.018	0.015	0.014	0.019	0.015
Test 5
Mean	0.001	0.084	0.001	0.116	0.003	0.082	0.003	0.102
SD	0.016	0.015	0.022	0.023	0.017	0.012	0.016	0.018
Second-order
${\overline{\mathrm{\theta }}}^{(2)}$	—	—	0.001	0.082	—	—	0.009	0.067
${\mathrm{Var}(\mathrm{\theta }}^{(2)})$	—	—	−0.009	0.096	—	—	−0.008	0.082
Loading
β1	0.011	0.037	—	—	0.006	0.025	—	—
β2	0.005	0.029	—	—	0.000	0.032	—	—
β3	−0.001	0.022	—	—	0.003	0.039	—	—
β4	0.002	0.026	—	—	−0.001	0.023	—	—
β5	−0.003	0.034	—	—	0.002	0.026	—	—
Residual
Mean	0.003	0.047	0.001	0.067	−0.004	0.044	0.016	0.058
SD	0.006	0.007	0.015	0.010	0.004	0.007	0.014	0.016

Note. RMSE = root mean square error; Second-order = second-order latent trait; Loading = factor loading; Residual = residual variance; — = not applicable because of model constraints.

Table 3 summarizes the parameter recovery for the nonlinear (quadratic) higher-order mixture Rasch model with respect to the bias and RMSE for a sample size of 2,000. The bias values were close to zero for all conditions. For the 20-item test length, the mean RMSE was between 0.036 and 0.110 for all estimators in the majority class and between 0.036 and 0.135 for those in the minority class, whereas for the 30-item test length, the mean RMSE was between 0.040 and 0.099 in the majority class and between 0.040 and 0.117 for those in the minority class. The difference in parameter recovery between the two test lengths was not apparent, and the majority class presented a better parameter recovery than the minority class.

Table 3.

Parameter Recovery for the Nonlinear Higher-Order Mixture Rasch Model With a Sample Size of 2,000.

Test length	20				30
Class	Majority		Minority		Majority		Minority
Criterion	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
Parameter
Difficulty
Test 1
Mean	0.020	0.092	0.020	0.123	−0.002	0.087	−0.002	0.114
SD	0.025	0.017	0.020	0.020	0.018	0.014	0.023	0.020
Test 2
Mean	0.030	0.098	0.030	0.130	0.011	0.085	0.011	0.114
SD	0.030	0.017	0.025	0.021	0.014	0.012	0.019	0.016
Test 3
Mean	0.027	0.096	0.027	0.126	0.003	0.092	0.003	0.111
SD	0.030	0.017	0.024	0.019	0.017	0.012	0.016	0.018
Test 4
Mean	0.026	0.098	0.026	0.133	0.003	0.091	0.003	0.117
SD	0.024	0.015	0.031	0.026	0.018	0.014	0.020	0.017
Test 5
Mean	0.028	0.095	0.028	0.128	0.009	0.086	0.009	0.113
SD	0.021	0.016	0.026	0.025	0.018	0.016	0.020	0.015
Second-order
${\overline{\mathrm{\theta }}}^{(2)}$	—	—	0.001	0.036	—	—	0.006	0.051
${\mathrm{Var}(\mathrm{\theta }}^{(2)})$	0.029	0.110	0.009	0.135	−0.016	0.099	−0.012	0.100
Loading
Linear
β11	—	—	—	—	—	—	—	—
β12	0.010	0.045	—	—	0.005	0.040	—	—
β13	0.000	0.048	—	—	0.012	0.061	—	—
β14	0.016	0.055	—	—	0.011	0.041	—	—
β15	0.015	0.049	—	—	−0.004	0.049	—	—
Quadratic
β21	−0.008	0.039	—	—	0.000	0.048	—	—
β22	−0.004	0.044	—	—	−0.006	0.046	—	—
β23	−0.010	0.043	—	—	−0.005	0.048	—	—
β24	0.001	0.036	—	—	0.001	0.049	—	—
β25	−0.023	0.048	—	—	−0.009	0.047	—	—
Residual
Mean	−0.001	0.080	0.000	0.121	0.013	0.073	0.003	0.100
SD	0.016	0.011	0.013	0.012	0.004	0.005	0.022	0.014

Note. RMSE = root mean square error; Second-order = second-order latent trait; Loading = factor loading; Residual = residual variance; — = not applicable because of model constraints.

Table 4 summarizes the parameter recovery in the quadratic higher-order mixture Rasch model with a sample size of 3,000. All of the bias values were close to zero for all conditions. For the 20-item test length, the mean RMSE was between 0.030 and 0.082 in the majority class and between 0.030 and 0.101 in the minority class, whereas for the 30-item test length, the mean RMSE was between 0.030 and 0.077 in the majority class and between 0.030 and 0.094 in the minority class. Parameter recovery patterns similar to those in the short test length were observed in the 30-item test, a larger sample size corresponded to more accurate model parameter estimates, and the parameter estimation was less affected by the test length. In summary, the linear higher-order mixture Rasch model yielded better parameter estimations compared with the quadratic higher-order mixture Rasch model, which was demonstrated by including the same 2,000 examinees that were used to generate item responses. Furthermore, the WinBUGS computer program with MCMC methods produced satisfactory parameter recovery for both the linear and nonlinear higher-order mixture Rasch models independent of sample size and test length.

Table 4.

Parameter Recovery for the Nonlinear Higher-Order Mixture Rasch Model With a Sample Size of 3,000.

Test length	20				30
Class	Majority		Minority		Majority		Minority
Criterion	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
Parameter
Difficulty
Test 1
Mean	0.010	0.075	0.010	0.100	0.009	0.067	0.009	0.088
SD	0.017	0.011	0.016	0.014	0.011	0.011	0.017	0.013
Test 2
Mean	0.010	0.076	0.010	0.096	0.015	0.072	0.015	0.091
SD	0.017	0.011	0.021	0.018	0.009	0.009	0.018	0.014
Test 3
Mean	−0.001	0.074	−0.001	0.094	0.016	0.070	0.016	0.093
SD	0.013	0.011	0.013	0.010	0.011	0.011	0.016	0.015
Test 4
Mean	0.008	0.076	0.008	0.098	0.012	0.070	0.012	0.086
SD	0.022	0.012	0.015	0.013	0.010	0.010	0.019	0.013
Test 5
Mean	0.008	0.074	0.008	0.101	0.006	0.077	0.006	0.094
SD	0.016	0.011	0.017	0.011	0.014	0.011	0.014	0.016
Second-order
${\overline{\mathrm{\theta }}}^{(2)}$	—	—	0.001	0.039	—	—	−0.003	0.030
${\mathrm{Var}(\mathrm{\theta }}^{(2)})$	−0.006	0.082	0.003	0.093	−0.024	0.072	−0.029	0.081
Loading
Linear
β11	—	—	—	—	—	—	—	—
β12	0.012	0.038	—	—	0.012	0.040	—	—
β13	0.007	0.039	—	—	0.019	0.046	—	—
β14	0.011	0.038	—	—	0.017	0.044	—	—
β15	0.002	0.030	—	—	0.022	0.045	—	—
Quadratic
β21	0.000	0.032	—	—	0.000	0.030	—	—
β22	−0.005	0.039	—	—	−0.010	0.041	—	—
β23	0.003	0.037	—	—	−0.009	0.038	—	—
β24	−0.005	0.041	—	—	−0.008	0.043	—	—
β25	0.004	0.041	—	—	−0.006	0.033	—	—
Residual
Mean	0.003	0.067	0.011	0.096	−0.004	0.058	−0.003	0.071
SD	0.017	0.005	0.024	0.010	0.005	0.012	0.019	0.006

Note. RMSE = root mean square error; Second-order = second-order latent trait; Loading = factor loading; Residual = residual variance; — = not applicable because of model constraints.

The recovery of group membership and individual ability for all conditions under both the linear and quadratic higher-order mixture Rasch models is presented in Table 5. The linear higher-order mixture Rasch model provided a more accurate estimation of the five first-order latent traits than the second-order latent trait, the long test length provided more precise estimations for both orders of latent traits and a higher correct classification rate, and the sample size had only a slight impact on the person parameter recovery. Note that the minority class presented a slightly less accurate estimation of the second-order latent trait and a lower correct classification rate compared with the majority class because of the higher RMSE values for item parameter estimates. The same conclusions can be drawn for the quadratic higher-order mixture Rasch model, although the estimate of the second-order latent trait was slightly more accurate than the estimates for the corresponding five first-order latent traits for the short test length. In addition, the estimation of the second-order latent trait in the minority class was substantially improved in the quadratic higher-order mixture Rasch model compared with that in the linear higher-order mixture Rasch model. Such findings provide plausible justification for the use of a quadratic higher-order mixture IRT model when the goal is to improve the measurement precision of the second-order latent trait for the minority class simultaneously without a substantial loss of estimation quality for the majority class.

Table 5.

Statistical Summary of the Person Parameter Recovery in Higher-Order Mixture Rasch Models.

Model	Linear				Quadratic
Sample size	1,000		2,000		2,000		3,000
Test length	20	30	20	30	20	30	20	30
Criterion
RMSE for the first-order latent trait
Test 1	0.429	0.371	0.426	0.371	0.520	0.443	0.517	0.442
Test 2	0.441	0.383	0.441	0.381	0.524	0.441	0.521	0.441
Test 3	0.455	0.391	0.454	0.390	0.526	0.447	0.526	0.445
Test 4	0.463	0.399	0.464	0.397	0.531	0.450	0.529	0.448
Test 5	0.473	0.403	0.469	0.404	0.531	0.449	0.527	0.448
RMSE for the second-order latent trait
Majority class	0.472	0.439	0.468	0.436	0.498	0.486	0.501	0.483
Minority class	0.613	0.610	0.613	0.607	0.448	0.427	0.448	0.433
Correct classification rate
Majority class	0.906	0.925	0.901	0.920	0.899	0.920	0.888	0.916
Minority class	0.727	0.820	0.763	0.859	0.724	0.821	0.760	0.840

Note. RMSE = root mean square error.

Simulation Study 2: Consequences of Fitting a Mixture Bifactor Model to Data Generated From the Higher-Order Mixture 2PLM or 3PLM

In this section, a comparison is performed between the generation of the higher-order mixture 2PLM or 3PLM and its corresponding mixture bifactor model with respect to parameter recovery. Table 6 shows the mean RMSE values for the item parameter estimates and latent trait estimates and the class membership percentages that were correctly classified when the higher-order mixture 2PLM or 3PLM and the mixture bifactor model were fit to the data generated from the higher-order mixture 2PLM or 3PLM. The higher-order mixture 2PLM and 3PLM recovered the item parameters better than their corresponding mixture bifactor models because the mean RMSE values were relatively smaller in the higher-order mixture 2PLM and 3PLM. The item difficulty parameter estimations appeared less accurate than the other item parameters in the mixture bifactor model because the differences in the mean RMSE values for the difficulty parameter estimates between the generating and misused models were relatively larger. Although not shown in Table 6, the mixture bifactor model had higher bias values (in the absolute values) for the item parameter estimates compared with the higher-order mixture IRT model across all conditions. Furthermore, the discrimination parameters were underestimated, and for example, when the responses of examinees to the five 20-item and 30-item tests followed the higher-order mixture 2PLM, the bias values were between −0.699 and −0.028 (M = −0.292) and between −0.655 and 0.000 (M = −0.278), respectively. Accordingly, disregarding the relationships between the second- and first-order latent traits in the mixture bifactor model had substantial impacts on the item parameter estimations.

Table 6.

Statistical Summary of the Comparison Between Higher-Order Mixture IRT Models and Mixture Bifactor Models.

Model	2PLM				3PLM
Approach	Higher-ordermixture		Mixturebifactor		Higher-order mixture		Mixturebifactor
Test length	20	30	20	30	20	30	20	30
Parameter
Difficulty	0.161 (0.088)	0.155 (0.106)	0.551 (0.400)	0.516 (0.460)	0.226 (0.121)	0.220 (0.133)	0.580 (0.386)	0.565 (0.385)
Discrimination	0.123 (0.046)	0.113 (0.059)	0.312 (0.158)	0.297 (0.215)	0.181 (0.081)	0.164 (0.080)	0.309 (0.146)	0.297 (0.133)
Pseudo-guessing	—	—	—	—	0.019 (0.005)	0.014 (0.005)	0.024 (0.006)	0.016 (0.005)
Factor loading	0.031 (0.011)	0.026 (0.007)	—	—	0.037 (0.008)	0.034 (0.007)	—	—
First-order latent trait
Test 1	0.439	0.380	0.644	0.590	0.514	0.450	0.685	0.645
Test 2	0.458	0.395	0.610	0.555	0.549	0.479	0.656	0.608
Test 3	0.463	0.392	0.601	0.548	0.539	0.465	0.652	0.609
Test 4	0.457	0.401	0.628	0.604	0.538	0.473	0.685	0.628
Test 5	0.436	0.391	0.706	0.705	0.519	0.464	0.749	0.712
Second-order latent trait	0.558	0.528	0.555	0.526	0.602	0.567	0.599	0.566
Correct classification rate	0.925	0.958	0.925	0.958	0.895	0.933	0.895	0.933

Note. 2PLM = two-parameter logistic model; 3PLM = three-parameter logistic model; RMSE = root mean square error. Mean RMSE was calculated for the item and latent trait parameters; the value in the parentheses indicates the standard deviation of the RMSE; — = not applicable because of model constraints.

For the person parameter recovery comparisons, the higher-order mixture 2PLM and 3PLM provided more precise estimations for the first-order latent traits compared with the corresponding mixture bifactor models. However, the differences between the two types of models in recovering the second-order latent trait and class membership were small because of the similar resulting values. A less accurate estimation for the item parameters and the first-order latent traits in the mixture bifactor model was expected because the variability of factor loadings between the second- and first-order latent traits should be considered but was ignored, which influenced the variability of the first-order residuals (or specific factors) and in turn resulted in biased estimates of the first-order latent traits and item parameters.

Although the second-order latent trait and class membership were not influenced substantially by the use of the misleading mixture bifactor model, the effects of ignoring the differential factor loadings on the item parameter and person parameter estimations were not trivial because they compromised the inferences related to the performances of examinees on each test and led to an equivocal assessment of the latent differential item functioning when equal factor loadings were mistakenly constrained in the mixture bifactor model. In addition, a greater test length and a simpler model (i.e., the 2PLM) produced better item parameter and latent trait estimations as well as a higher classification accuracy in the higher-order mixture IRT models.

Two Empirical Studies

Example 1: High-Stakes Entrance Examination

Students in Taiwan who wish to enter senior high school must take the Basic Competence Test for Junior High School Students (BCT), which consists of the five subjects: Chinese, Mathematics, English, Social Sciences, and Natural Sciences. The performances on these five subjects are merged into a single score that represents the overall performance in essential knowledge. Therefore, a higher-order structure of latent traits is necessary to obtain the overall assessment of examinees, and the second-order latent trait estimation is used for the purpose of admitting the examinees to senior high schools.

The Rasch model was used to calibrate the model parameters when developing the BCT. In this study, a BCT data set was used to demonstrate the application of the higher-order mixture Rasch model, which included 48, 33, 45, 63, and 58 items that tested the knowledge of Chinese, Mathematics, English, Social Sciences, and Natural Sciences, respectively. All of the items were arranged in multiple-choice format. The five first-order latent traits were measured by each of the tests and constituted a second-order latent trait of “overall academic ability.” A total of 3,000 examinees were randomly selected from a population of over 300,000 examinees and used for the analysis. Following practices that are normally used to analyze the BCT data, the Rasch model was adopted, and an assumption of metric invariance was appropriate in this analysis. Note that this approach was justifiable in this case but should be used with caution in other cases.

We focused on two questions when performing the model comparisons. First, is a linear or quadratic higher-order mixture Rasch model more appropriate for fitting the data? Second, how many latent classes should be used to explain the diverse performance on the item level resulting from different response patterns among examinees? In this analysis, one-, two-, and three-class models were considered, and as a result, a total of six competing models (two higher-order mixture Rasch models × three types of latent classes) were used to fit the data. The linear higher-order mixture Rasch model with two latent classes was selected as the best-fitting model because of its smaller BIC value (BIC = 694,100) compared with that of the other competing models (BIC values were between 694,200 and 705,600). The majority class contained 61% of the examinees, and the minority class contained 39% of the examinees. The difference in the mean second-order latent trait between the two latent classes was extremely small (0.003), and the five factor loading estimates were 0.47, 0.74, 0.49, 0.49, and 0.52 for Chinese, Mathematics, English, Social Sciences, and Natural Sciences, respectively.

Because the item difficulty parameters were estimated separately for the two latent classes and the difference in magnitude is statistically tested, the highest posterior density (HPD) interval was calculated to assess whether the difference in magnitude was significantly different from zero (Box & Tiao, 1973). With a nominal $\mathrm{\alpha }$ value of 0.05, if the HPD interval of the difference in magnitude for the studied item included zero, then scalar invariance was identified on that item; otherwise, the item was considered to be the qualitative difference between the two classes (Cho & Cohen, 2010; Samuelsen, 2008).

The analysis indicated that 38 Chinese items, 31 Mathematics items, 38 English items, 52 Social Science items, and 42 Natural Science items were found to violate the assumption of scalar invariance. The mean difference in magnitude was 0.47 (0.00-1.22) for Chinese, 0.61 (0.01-1.68) for Mathematics, 0.68 (0.00-1.83) for English, 0.51 (0.06-1.45) for Social Sciences, and 0.54 (0.02-1.52) for Natural Sciences. Because the statistical significance of the HPD method is substantially affected by the sample size, the difference in magnitude should be considered as a measure of the effect size for item bias. Wang (2008) suggested that an item with a difference in magnitude greater than 0.5 logits would yield substantially practical impacts on the person parameters. In this analysis, approximately 48% of the test items had a magnitude of more than 0.5 logits and were treated as consequences of the different response patterns between the two latent classes. Identifying such a large number of items exhibiting a significant difference in magnitude in the higher-order mixture Rasch model was not surprising because the differences among the latent classes would be maximized by the latent class approach and a number of additional items with qualitative differences could be observed using the latent classes than a conventional analysis using the manifest groups (Cho & Cohen, 2010; Cohen & Bolt, 2005).

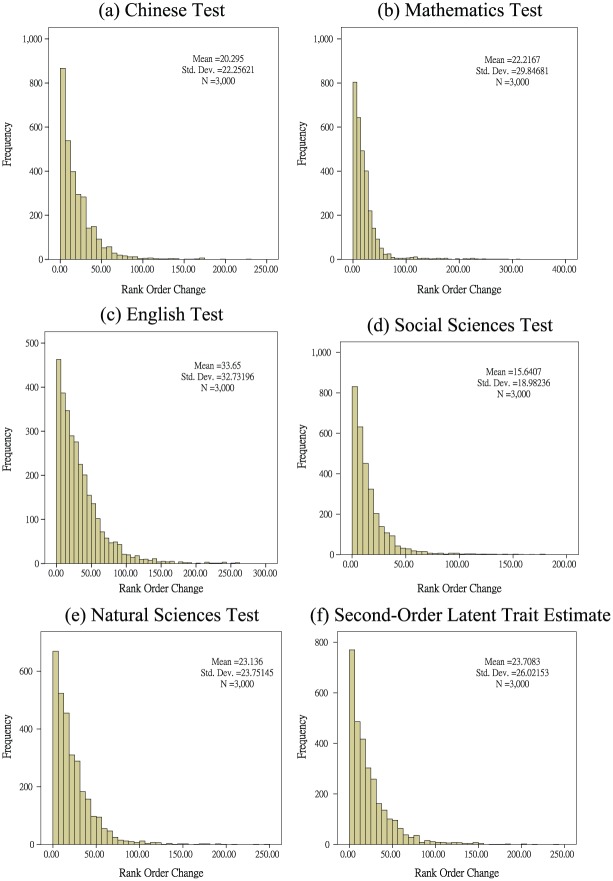
Because the BCT is a high-stakes examination, the consequences of using a model that provides misleading results because it disregards the mixtures of latent classes should be further investigated. The students’ ability estimates were calculated using the linear higher-order Rasch model with two latent classes (i.e., the best-fitting model) and without mixtures for both the second- and first-order latent traits. These estimates were then ranked in order for comparison purposes. The rank order changes in the absolute values between the ability estimates obtained from the two models were calculated, and large rank-order changes indicated that the practical impact cannot be neglected. Figure 1 shows the rank-order changes in the five first-order latent traits and the second-order latent trait. The maximum rank-order changes were 288, 311, 262, 176, and 248 for the five first-order latent traits measured by the Chinese, Mathematics, English, Social Sciences, and Natural Sciences tests, respectively, and 241 for the second-order latent trait. The impact of rank-order changes on the person parameters was not trivial because expanding the number of examinees from 3,000 to the original 300,000 produced the maximum rank-order changes, which were as high as 28,800, 31,100, 26,200, 17,600, and 24,800 for the five subjects and 24,100 for the overall performance. In summary, the results obtained from the two models were significantly different, and the test fairness would be substantially threatened if mixtures of latent classes were disregarded by using a regular higher-order Rasch model to fit the BCT data.

Figure 1.

Rank-order changes in the BCT between the linear high-order Rasch models with two latent classes and without mixtures.

Example 2: Large-Scale Survey for Basic Ability Assessment

A longitudinal large-scale assessment supported by the Taiwan Education Panel Survey (TEPS) was administered to students from the 7th to the 12th grades in Taiwan using four measurements. Similar to international large-scale assessments, the TEPS was designed to measure the students’ basic analysis, mathematics, reading, and science abilities; therefore, the four content domains were treated as measures of the first-order latent traits and can constitute an overall assessment of basic ability to represent the second-order latent trait. The first measurement was analyzed for demonstration purposes, and the four basic abilities of analysis, mathematics, reading, and science were measured using 27, 10, 20, and 10 multiple-choice items, respectively. A random sample of 3,000 examinees’ responses to these items was included to evaluate whether a mixture of latent classes occurred among the examinees. Because four first-order latent traits were included in this example, a linear relationship structure between both orders of latent traits was considered under a variety of higher-order mixture IRT models and mixture bifactor models.

Several approaches were adopted to select the model with the best fit to the data. First, higher-order mixture IRT models that followed the item response functions of the 1PLM (i.e., the Rasch model), 2PLM, and 3PLM with three mixture conditions (one, two, and three latent classes) were fit to the data to determine whether item discrimination and pseudo-guessing parameters were needed to calibrate and identify the number of latent classes. Second, we compared the model selected in the first step with its corresponding mixture bifactor model to examine whether the assumption of identical factor loadings was satisfied.

The results of the model comparisons showed that the higher-order mixture 3PLM with two latent classes yielded a smaller BIC value (BIC = 210,500) than the other higher-order mixture IRT models (BIC values between 210,600 and 215,100). Next, the higher-order mixture 3PLM with two latent classes was compared with its corresponding mixture bifactor model, and the results indicated that the latter model had a higher BIC value (BIC = 210,600); therefore, the former model was the final model of choice. In the higher-order mixture 3PLM, the majority (high-proficiency) class had a mixing proportion of 58% with an estimated mean $\mathrm{\theta }$ of 1.83 and the minority (low-proficiency) class had a mixing proportion of 42% with a constrained zero mean $\mathrm{\theta }.$ The difference in magnitude in the absolute values between the two classes was between 0.01 and 1.42 (M = 0.39) for the discrimination parameters, between 0.01 and 4.35 (M = 0.65) for the difficulty parameters, and between 0.03 and 0.11 (M = 0.07) for the pseudo-guessing parameters, which suggested that the two latent classes exhibited substantial diverse response patterns. In addition, the factor loadings for the four subscales of analysis, mathematics, reading, and science were estimated as 0.98, 0.72, 0.94, and 0.81 for the high-proficiency class, respectively, and 0.90, 0.87, 0.94, and 0.87, respectively, for the low-proficiency class, which supported the violation of metric invariance.

When the background information for the examinees are accessible, the association analysis between latent class membership and manifest group membership could be investigated. Such an analysis would be useful for explaining the potential causes of the occurrences of latent classes (Cho & Cohen, 2010; Cho et al., 2014; Dai, 2013). Three types of student characteristics, including the gender (male and female students), residence regions (urban and rural regions), and school types (public and private schools), were used to associate the class membership with the statistical hypothesis testing. As shown in Table 7, a nonsignificant association between the latent class membership and students’ gender was observed (${\mathrm{\chi }}^2=0.68,$p = .409), whereas the reverse was observed for the association with the students’ residence regions (${\mathrm{\chi }}^2=40.63,$p = .000) and school types (${\mathrm{\chi }}^2=40.87,$p = .000). For the students’ residence regions, a high percentage of rural students were classified into the low-proficiency class (62.8%), whereas most of the students residing in urban regions were classified in the high-proficiency class (60.2%). For the school types, a higher percentage of the students in private schools were classified in the high-proficiency class (74.2%) compared with the public school students (56.6%). Accordingly, the occurrence of latent classes may have been dominated by the residence regions of the students, and the diverse response strategies employed by the urban and rural students may cause differential response patterns. Note that the results should be interpreted with caution because the sample of students residing in the rural region was considerably smaller compared with the sample of students residing in the urban region.

Table 7.

Association Between the Proficiency Classes and Students’ Characteristics.

Characteristic	Proficiency	Low	High	Total	${\mathrm{\chi }}^2$
Gender	Male	655 (42.0%)	904 (58.0%)	1,559	0.683
	Female	584 (40.5%)	857 (59.5%)	1,441
	Total	1,239	1,761	3,000
Residence region	Rural	125 (62.8%)	74 (37.2%)	199	40.693***
	Urban	1,114 (39.8%)	1,687 (60.2%)	2,801
	Total	1,239	1,761	3,000
School type	Public	1,146 (43.4%)	1,493 (56.6%)	2,639	40.870***
	Private	93 (25.8%)	268 (74.2%)	361
	Total	1,239	1,761	3,000

Note. The values in parentheses indicate the proportion for the two latent classes within each level of students’ characteristic.

^***p < .001.

Finally, we compared the results of the latent trait and membership estimates obtained from the higher-order mixture 3PLM with two classes (i.e., the best-fitting model) with those obtained from its corresponding mixture bifactor model to investigate the consequences of imposing identical factor loadings between the second- and first-order latent traits. The classification consistency rate between the two models was as high as 0.97; however, the rank-order changes between the two models were substantial for both the second- and first-order latent traits. The maximum rank-order changes were 174 (M = 28), 280 (M = 30), 212 (M = 24), and 230 (M = 28) for the four first-order latent traits measured according to the subscales of analysis, mathematics, reading, and science, respectively, and 1,063 (M = 135) for the second-order latent trait, which suggested that different sets of factor loadings between the second- and first-order latent traits were necessary and ignoring the differential factor loadings in the mixture bifactor model had substantial impacts on the latent trait estimations. The large differences in the second-order latent trait estimates between the two models may have been caused by the use of short tests to measure certain subjects because these tests were associated with imprecise person parameter estimations.

Conclusions and Discussion

Higher-order mixture IRT models were proposed for tests that measure higher-order latent traits and for data with mixtures of latent classes. These models can be viewed as a combination of an IRT model, a higher-order factor model, and a finite discrete latent class model. In real testing situations, the latent traits measured by multiple tests are often observed to have a higher-order structure, and manifest groups of examinees may be not attainable or reliable. Therefore, in this study, we provided a variety of higher-order mixture IRT models to address this practical concern and investigate the different response patterns among classes. Such model extensions not only involve variations of previous IRT models but also provide an innovative integration of higher-order IRT models and mixture IRT models to examine how latent classes can function with a higher-order structure on latent traits.

The developed higher-order mixture IRT models can provide greater flexibility if the linear and nonlinear relationships between the second- and first-order latent traits are accommodated and if mixtures of latent classes are allowed to occur on different orders of latent traits. Various relationships between the higher- and lower-order latent traits were demonstrated using the mixture Rasch model because this model has been widely applied in data analyses in the literature and has better measurement characteristics than other multiparameter IRT models. In addition, a higher-order multiparameter IRT model that incorporates mixtures of latent classes on different orders has been developed in this study to expand the generality of higher-order mixture IRT models. Therefore, current factor mixture models or mixture IRT models, including mixture bifactor models (Cho et al., 2014), can be treated as special cases of the developed higher-order mixture IRT models.

In the two simulation studies, parameter recovery in the new models was evaluated using WinBUGS software and MCMC methods. For the first simulation study, the results indicated that the performance of the higher-order mixture Rasch model was satisfactory for both the linear and nonlinear approaches, although the nonlinear approach was slightly inferior to the linear approach with regard to parameter recovery. For both approaches, a larger sample size was associated with higher accuracy in the item parameter estimations and the majority class (high proportion of examinees) always exhibited more accurate parameter estimations than the minority class (low proportion of examinees). A longer test length corresponded to better person ability recovery and group membership recovery. The linear higher-order mixture Rasch model yielded better person parameter recovery compared with the quadratic higher-order mixture Rasch model for the first-order latent traits, and the quadratic higher-order mixture Rasch model yielded better second-order latent trait recovery in the minority class compared with the linear higher-order mixture Rasch model.

The second simulation study manipulated multiparameter IRT models and allowed both the second- and first-order latent traits to include latent classes, which relaxed the assumptions of both scalar and metric invariance. Furthermore, we compared the results from the higher-order mixture 2PLM or 3PLM with the results derived from the mixture bifactor model that was misleadingly fit to the data generated from the higher-order mixture 2PLM or 3PLM. The results indicated that improved item parameter recovery occurs with the higher-order mixture 2PLM and 3PLM compared with their corresponding mixture bifactor models, which tended to increase the vulnerability of item difficulty parameters and underestimate the item discrimination parameters when used to fit the data. As for person parameters, imposing a constraint on identical factor loadings between the second- and first-order latent traits in the mixture bifactor model influenced the first-order latent trait estimation to a greater degree than the second-order latent trait and class membership estimation. The effects of fitting the misleading model on the parameter estimations were substantial because the test validity and examinee performance inferences were threatened.

The applications of higher-order mixture IRT models were illustrated by a high-stakes test for senior high school admission and a large-scale basic ability assessment for a longitudinal survey. The first empirical example analysis indicated that there were two latent classes and the linear relationship between the second- and first-order latent traits was sufficient to account for the hierarchical structures in latent traits. Nearly half of the test items were found to violate scalar invariance, and ignoring the mixture of latent classes in the data by fitting a standard higher-order Rasch model resulted in more severe rank-order changes in the person parameters for both the second- and first-order latent traits, which compromised the test fairness. In this demonstration, the Rasch model was considered in the data analysis following the testing development practices in the BCT; however, we suggest that the results should be interpreted with caution because of the assumptions related to measurement invariance, which may affect the model parameter calibration quality (Alexeev, Templin, & Cohen, 2011). In addition, for privacy policy reasons, the demographic variables related to the examinees were not available in the BCT; therefore, the potential causes underlying the occurrence of latent classes cannot be further investigated.

The second empirical example analysis was presented to illustrate the application of the higher-order mixture multiparameter IRT models and provided a comparison between the developed models with the constrained mixture bifactor model. The analysis results support the importance of the pseudo-guessing and discrimination parameter estimations and indicate that constraints on both the scalar and metric invariance should be relaxed. In addition, two latent classes, denoted as the high- and low-proficiency classes, were observed to associate with the students’ residence regions and school types. An inspection of the percentage of students classified in the two classes showed that the urban students were more likely to be classified in the high-proficiency class and the rural students were more likely to be classified in the low-proficiency class. The mixture bifactor model that constrained identical factor loadings between the second- and first-order latent traits had a high classification consistency rate with the higher-order mixture 3PLM but a nontrivial impact on the latent trait estimations because of the large rank-order changes. For the items with significant differences between the two latent classes in both the empirical example analyses, a close examination of the item characteristics and test contents using content experts will help characterize the response patterns of the latent classes; however, this is beyond the scope of this study.

Partial credit is often given to examinees when evaluating different degrees of performance in cognitive skills (e.g., PISA). The higher-order mixture IRT models for dichotomous items can easily and directly generalize to higher-order mixture IRT models for polytomous items. Considering the partial credit model (PCM; Masters, 1982) as an example, we can formulate a higher-order mixture PCM by integrating the PCM with mixture and higher-order models, which can be expressed as

$$\log \left(\frac{P_{n{g}_1{g}_2\mathrm{ijv}}}{P_{n{g}_1{g}_{2}i(j-1)v}}\right)=[{\mathrm{\theta }}_{n{g}_1{g}_{2}v}^{(1)}-({\mathrm{\zeta }}_{g_1{g}_2\mathrm{iv}}+{\mathrm{\tau }}_{g_1{g}_2\mathrm{ijv}})],$$

where $P_{n{g}_1{g}_2\mathrm{ijv}}$ and $P_{n{g}_1{g}_{2}i(j-1)v}$ are the probabilities of obtaining scores j and j− 1 on item i of test v for respondent n within classes $g_1$ and $g_2,$ respectively; ${\mathrm{\zeta }}_{g_1{g}_2\mathrm{iv}}$ is the overall difficulty parameter of item i in test v for classes $g_1$ and $g_2;$ and ${\mathrm{\tau }}_{g_1{g}_2\mathrm{ijv}}$ is the jth threshold parameter for item i of test v in classes $g_1$ and $g_2$. Higher-order mixture IRT models with higher generality can be used for novelty model extensions if an item response function can be appropriately defined for the data responses. Thus, assessments of the estimation efficiency of the polytomous-item type of higher-order mixture IRT models and evaluations of new model applications for data analysis are encouraged in the future.

In this study, two orders of latent traits and one second-order latent trait were formulated. Higher-order mixture IRT models are readily extended and can accommodate additional orders (more than two orders) and more than two second-order (higher-order) latent traits. In addition, multilevel IRT models have been developed to describe multilevel structures in populations (Fox, 2005), and multilevel higher-order IRT models have been proposed to account for hierarchies in both populations and latent traits (Huang, 2015; Huang & Wang, 2014). It is of great value to develop multilevel higher-order mixture IRT models that combine multilevel mixture IRT models (Cho & Cohen, 2010) and higher-order mixture IRT models into more general formulations. Such generalizations and extensions of mixture IRT models deserve further exploration.