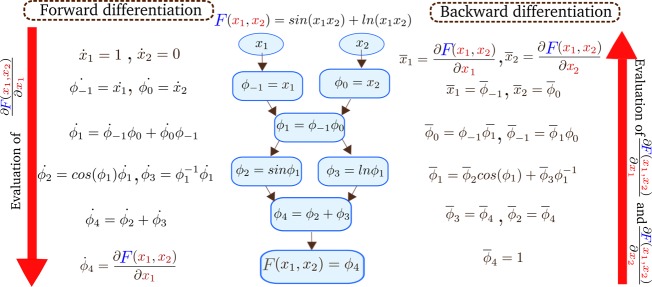
Figure 1.
The center depicts the computational graph of a simple function F(x1, x2) and its elementary operations. On the left and right, we illustrate the differentiation steps of forward and backward mode, respectively. In forward mode, the evaluation of the function at a given set of parameter and the derivative with respect to x1 is evaluated by computing the intermediate variables ϕi and their derivatives following the order of the computational graph using the chain rule. The direction of the evaluation is indicated by the left arrow. In backward mode, the function is evaluated first at a given value, and later the adjoints of all the intermediate variables are computed by iterating backward through the computational graph, indicated by the right arrow. Notice, in this mode, the partial derivatives of the function with respect to the two independent variables are computed together, whereas in forward mode each partial derivative of the function has to be evaluated separately. In this example, to compute the entire gradient, the number of operations in backward mode is smaller than in forward mode.