Comment on “Substrate Folding Modes in Trichodiene Synthase: A Determinant of Chemo- and Stereoselectivity”

Abstract

Wang et al. recently reported an in silico study of the trichodiene synthase (TDS) conversion of farnesyl diphosphate (FPP) to trichodiene (TD) (Wang et al., ACS Catal. 2017, 7, 5841–5846). Although the methods and level of theory used in that work are nearly identical to our own recent work on this system (Dixit et al., ACS Catal. 2017, 7, 812–818), Wang et al. reach rather different conclusions. The authors claimed to obtain a “very credible” mechanism for the biosynthesis of TD and optimized the optimal folding mode of FPP in the 1,6-ring closure in TDS. However, the folding mode of the FPP substrate that was presented contradicts well-established NMR and mass spectrometry data. Moreover, the authors make numerous incorrect statements regarding our earlier work.

Graphical abstract

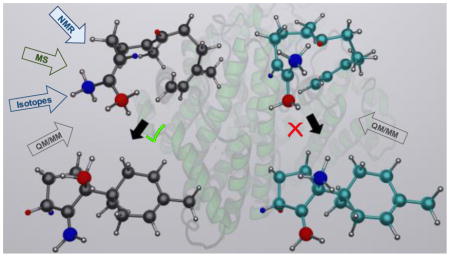
The purpose of this commentary is to point out several errors in the recent work of Wang et al.¹ on the biocatalysis in trichodiene synthase (TDS). These errors pertain to the claim of an “optimal” binding mode of the substrate farnesyl diphosphate (FPP), which, in fact, is inconsistent with experimental data, and numerous puzzling and plainly incorrect statements on our work that was published earlier in this Journal.² Importantly, the findings and key reaction steps appear to directly contradict the reaction pathway established by NMR isotope-labeling experiments.

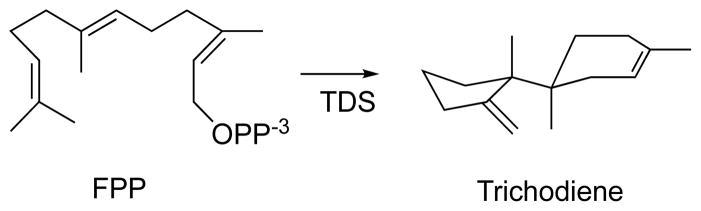
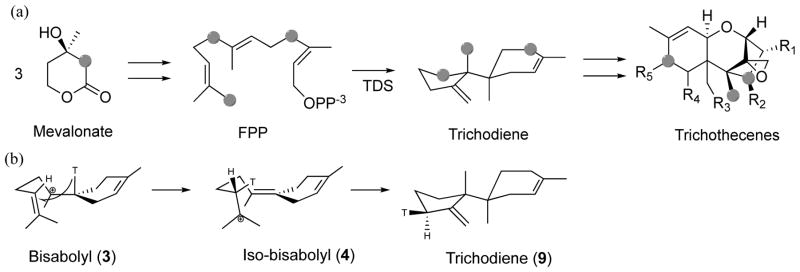
Previously, we reported on an extensive study utilizing a combined quantum mechanical and molecular mechanical (QM/MM)^3–4 method on the biosynthetic formation of trichodiene (TD) by TDS (Scheme 1), culminating from laborious and thorough work carried out in a period of over ten years.² In that study, we addressed numerous issues pertinent to the chemical control exerted by TDS to avoid by-product formation from a sequence of reactive carbocation intermediates, and highlighted several general catalytic principles that are potentially applicable to other terpenoid synthases. TDS has been extensively studied experimentally,^5–8 providing an unprecedented amount of data for judicious comparison and validation of theory.^9–10 TDS, as other terpenoid synthases, is extremely challenging to theoretical investigation because the precise, folded conformation of the linear substrate FPP in the binding pocket is unknown. There are multiple possible reaction channels leading to unwanted by-products, and it is necessary to use accurate quantum chemistry methods to treat the facile bond breaking and bond forming steps.^{2, 11–15} To overcome these difficulties, we have developed and reported in reference ² a systematic strategy to treat these biosynthetic processes computationally.^{14, 16–17}

Scheme 1.

Conversion of farnesyl diphosphate (FPP) to trichodiene by trichodiene synthase (TDS).

In a subsequent publication, Wang et al. attempted to address the important role of substrate binding in TDS, with a particular emphasis on stereoselectivity.¹ In that work, the authors followed essentially the same procedures, including exactly the same level of theory described in Ref. ², but started by docking the large, open structure of FPP directly into the active site. Then, the authors tried to delineate how this initial fold determines chemical specificity. Unfortunately, the report of Ref. ¹ contains egregious errors that we will address in the following, including (1) erroneous key results that directly contradict the previously established reaction pathway by NMR and mass spectrometric experiments, and (2) incorrect statements that, surprisingly, directly contradict the structures and written texts in Ref. ².

(1) Erroneous key results that contradict well-established experimental NMR data

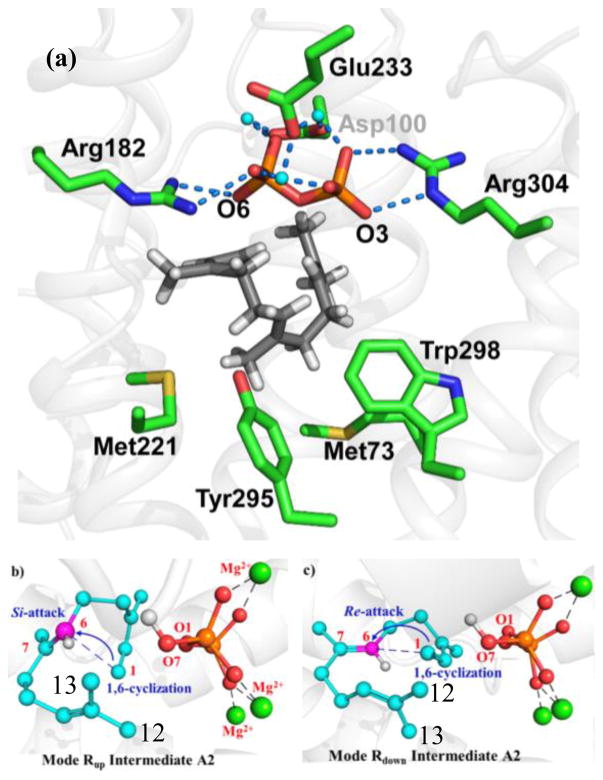
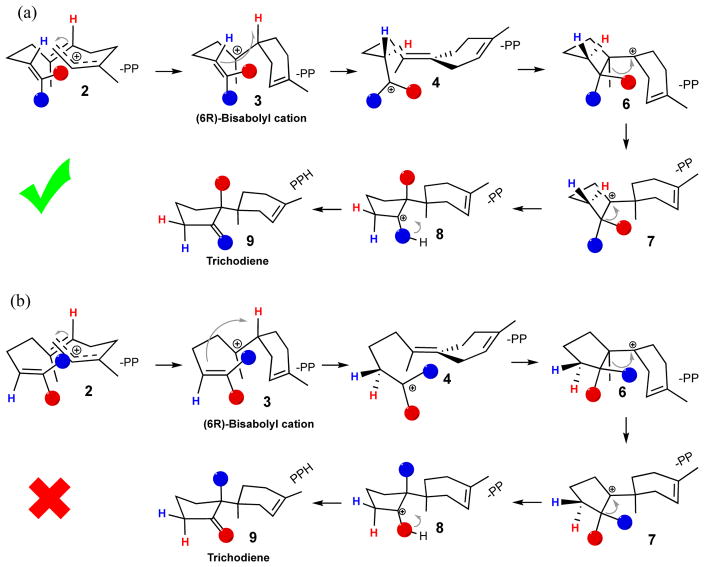
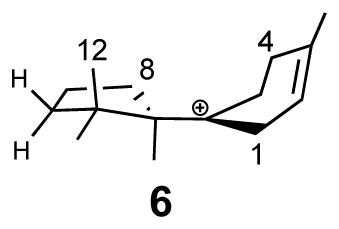
Wang et al. stated that the R_up conformation (Fig. 1b), a notation used in Ref. ¹, gives the most reasonable C-O bond dissociation profile, and thus is the favorable folded substrate conformation in TDS. Hence, mode R_up is the most likely productive folding mode. This conclusion was based on energetic considerations (see Fig. 2a in Ref. ¹), and indeed, was a main result of their work. Wang et al. utilized this conformation for FPP in their mechanistic studies. As a result, the C13-methyl group (C12 in Ref. 1) was transferred to C7 (Fig. S7 in Ref. 1). In contrast, it is, in fact, the C12-methyl group (standard numbering), trans to C9 of FPP, that migrates. This has been laboriously defined and elucidated by Cane and coworkers and others through extensive NMR and mass-spectrometry experiments, in which ¹³C-labeled mevalonate was used to generate labeled FPP, in turn, to form labeled TD (Scheme 2a).^{6, 8, 18–24} We further point out that it is well established that there is no free rotation around the C10–C11 bond prior to methyl group migration in the enzyme active site.¹⁹ Thus, C12 and C13 are non-equivalent. Note that the numbering for the C12/C13 atoms is inverted in Ref. ¹, but to leave no room for misunderstanding, C12 in Ref. ¹ is the methyl group “cis” to C9 of FPP, whereas the standard IUPAC style numbering for the cis carbon is C13 used in our and other publications.⁵ The correctly folded conformation used in our earlier work is shown schematically in Scheme 3a, whereas the incorrectly folded conformation used by Wang et al. is shown in Scheme 3b.

Figure 1.

Conformations of the Farnesyl cation prior to carbocation cyclization used in Ref. ² (a) (original Fig. 3b), and those in Ref. 1 (b) and (c) (original Fig. 2b and 2c in Ref. ¹). Notice that (b) shows the correct stereochemistry for the C1–C6 cyclization, yielding (6R)-bisabolyl cation, but the C13 methyl group cis to C9 is posed for migration. Shown in (c) is the conformation Wang et al. incorrectly assigned as that used in Ref. ², which “would directly lead to the formation of bisabolyl cation B with S configuration conflicted with the configuration demanded for the product”. Yet, on page 815 of Ref. ², it was clearly stated that “electrophilic attack at the C6–C7 double bond to produce (6R)-bisabolyl cation”. Reproduced with permission by the American Chemical Society.

Scheme 2.

NMR labeling patterns employed in the literature to determine the mechanism of the biosynthesis of trichothecenes. (a) ¹³C labeling (gray spheres) determines methyl migration patterns, while (b) Tritium labeling determines proton transfer stereochemistry. Only the depicted conformation in (b) gives the correct labeling patters, and not the one adopted by Wang et al.¹

Scheme 3.

Two different folded conformations of the hydrocarbon chain in the active site of TDS can both give the final product trichodiene. However, only the folding shown in (a) agrees with the labeling experiments given in Scheme 2. The distinguishable hydrogens are colored red and blue, while the distinguishable methyl groups are presented as red and blue spheres.

Due to the use of this incorrectly folded substrate conformation (Fig. 1b, Scheme 3b), the proton on the C6 carbon was transferred to the incorrect Re-face of C10 in Ref. 1, instead of Si. However, the use of a ³H-labeled FPP substrate [6-³H-12,13-¹⁴C]-farnesyl pyrophosphate unambiguously assigned the ³H-labeled TD in Scheme 2b as the exclusively product.¹⁹ Hence, both the proton and methyl transfer steps in the study by Wang et al. directly contradicted well-established stereochemistry from NMR and mass-spectrometry isotope-labeling experiments carried out by several groups: it is the Si-face, not Re, of C10 to which the proton on C6 migrates (Scheme 2b, 3a).^{6, 8, 18–24}

The contradiction of the results from Ref. ¹ with experiments specifically designed to answer the precise regio- and stereo-selectivity of hydrogen and methyl group migrations in TDS demonstrate that the conformation used in Ref. ¹ does not correspond to the correct initial Michaelis complex. On the other hand, the erroneous reaction pathways followed in Ref. ¹ (Scheme 3b) lend further support to our contention that the promiscuous binding in terpene synthases is one of the greatest challenges to theory due to weak interactions between the substrate and the hydrophobic pocket in the active site. In particular, the numerous weak dispersion interactions are difficult to model without using the most accurate quantum chemical methods, or dedicated dispersion correction schemes,²⁵ in conjunction with carefully parametrized QM/MM interaction terms.^26–27

(2) Incorrect statements of published work on TDS

For reasons that are puzzling to us, the authors of Ref. ¹ incorrectly quoted several direct statements and structures that are plainly contrary to those reported in Ref. ²; unfortunately, the incorrect statements were used as evidence to justify their erroneous findings discussed above. In Ref. ¹, Wang et al. stated that “Major et al. theoretically investigated the reaction pathway from cisoid 3R-NPP to TD derived from folding mode R_down”. These authors created and illustrated their R_down conformation that is duplicated in Fig. 1c, based on which they proclaimed that the cyclization step in our study “would directly lead to the formation of bisabolyl cation B with S configuration conflicted with the configuration demanded for the product”. There are at least two incorrect statements in this short paragraph of Ref. 1. First, we explicitly wrote, on page 815 of Ref. ², “electrophilic attack at the C6–C7 double bond to produce (6R)-bisabolyl cation” (3 in Ref. ²). Moreover, (6R)-bisabolyl cation 3 is clearly illustrated in Scheme 1, Figs. 1, 2, and 3 of our original paper.² We further note that only in this conformation, can the correct methyl migrations and proton transfer take place. Second, the simulations in Ref. ² were carried out with the so-called folding mode R_down, with the initial ring closure proceeding with an electrophilic attack on the Si-face of the C6–C7 double bond (Fig. 2). This results in the correct (6R)-bisabolyl cation. Wang et al. called this conformation “the conformation that Cane employed”, which is in fact deduced based on the extensive NMR data discussed above.^{6, 8, 18–24} The current correspondence is a re-affirmation of the modeling result for the Michaelis complex of TDS obtained in Ref. ².

Figure 2.

Ball-and-stick model of a snapshot configuration of the farnesyl pyrophosphate substrate in the Michaelis complex. The same three-dimensional structure reported in Fig. 3b of Ref. ² is shown, but at a different view angle. The figure shows the Farnesyl cation in a folded conformation to yield the correct regio- and stereochemistry along the entire reaction path leading to trichodiene and potentially all other observed by-products. Carbons C1, C6, C12, and C13 are marked.

Wang et al. further proceeded with the statement that “the modeling (of Ref. ²) was based on the docking pose of intermediate D with exo conformation instead of the endo conformation derived from mode R_up of substrate FPP.” Indeed, our simulations commenced with cation 6 (D in Ref. ¹). However, Wang et al. seemingly did not realize that the intermediate structure determined by X-ray diffraction and modeling was only used as the starting point for a series of modeling and optimization calculations that included more than 10,000 configurations. The structure adopted as a model for the Michaelis complex was chosen based on energetic and mechanistic considerations, an issue we have repeatedly addressed and warned in our general studies of enzymatic reactions in the past two decades.^{16, 28–36} Furthermore, we did not, and in fact, we never restrict the conformations of the substrate or the protein in computational studies of enzymatic processes, including the present conformational flexibility of the C9 methylene group. This group was indeed free to fluctuate between the so-called exo and endo forms. These substrate conformation fluctuations were in fact observed to take place frequently in our simulation, as the free energy barrier for such a flip is about 1–2 kcal/mol. Hence, it is inconsequential which ring conformation we started with, as long as it is docked correctly into the active site. If carried out properly, we suspect similar conformational fluctuations would be observed in other TDS simulations. What is crucial, however, is that the correct farnesyl cation conformation is used, and the one we obtained by retrobiosynthesis from cation 6 is shown in Fig. 1a and 2. Only this general conformation leads to agreement with all available experimental data.

A central question in terpenoid biosynthesis of natural products is the initial conformational state of the substrate of the linear FPP. There are numerous conformers coupled with 8 single bonds in FPP, which could yield a wide range of folded structures. A wonder of terpenoid biosynthesis is that each terpenoid synthase adopts a FPP conformation to generate one dominant natural product with precisely defined regio- and stereochemistry. Wang et al. criticize the protocol employed in our initial modeling of the Michaelis complex starting from the ligand bound X-ray crystal structure derived from cation 6 by contrasting their approach: “theoretical modeling starting from the native FPP substrate is more warrantable than that from a hypothetical intermediate.” Of the countless number of conformers of FPP, it is not clear which one may be considered as the “native FPP substrate” for a given enzyme configuration. Additionally, it is far from trivial to identify the dominating bound conformation of FPP. On the other hand, the intermediate structure (cation 6) that we employed as a starting point resembles the final product configuration, and it is a rather rigid molecule that is simpler to model. This intermediate contains key information regarding the mechanistic flow of the biosynthesis. Our structure-based retro-biosynthesis approach commences with docking, energy minimization, and molecular dynamics simulations of a key semi-rigid intermediate (cation 6). Subsequently, the intermediate is allowed to slowly relax to the FPP substrate in several sequential, mechanistically reverse, free energy molecular dynamics steps. This procedure provides the potentially correct fold of the substrate in the Michaelis complex, whose correctness can only be validated by the energetics of reaction pathway and the correct formation of the major and numerous side products.

Very few crystal structures exist of the native Michaelis complex of enzymes, since it will readily be decomposed into the product.²⁹ Thus, the modeling of the initial substrate conformation and substrate-protein interactions is always necessary, and often, this is the determining factor for the quality of the computational approach, rather than a particular QM model used, be it ab initio wave function theory, density functional theory, or semiempirical methods. Unfortunately, there is no unique way of approaching this question, because vastly different structures and biochemical data are available for different enzymes. We have thoroughly discussed approaches to address this important question in the past,^{16, 28–36} and the work presented in Ref. ² provided yet another strategy. The procedures on substrate conformation modeling, and the subsequent conclusions reached by Wang et al. may serve as a counter-example, illustrating the pitfalls of improperly modeling the initial Michaelis complex.¹ Indeed, one should include all experimental information as far as modeling is concerned, since enzyme Michaelis complex construction has not yet reached a stage where it can predict function in an entirely ab initio manner.

Enzyme catalysis

We finally comment on the free energy profile obtained by Wu and co-workers, which contains what may be called death-traps in terpenoid biochemistry. The conversion of bisabolyl cation (3) to the subsequent intermediates has a significant barrier according to Wu and co-workers. This is problematic since this bottleneck appears after the key intermediate (3), which branches into pathways leading to many byproducts.² This issue of the life-time of 3 has been carefully discussed in Ref. ². We stress that a significant barrier along the carbocation reaction coordinate poses intractable problems for the cyclization cascade, due to the extremely high reactivity of carbocations. In fact, the carbocation chemistry has been shown to proceed with small barriers or to be barrierless processes.^{2, 11, 13–14, 16, 37} The appearance of a key mechanistic branching intermediate, bisabolyl cation 3, immediately before a bottle-neck in the calculations of Ref. ¹ can only increase the likelihood of by-product formation in the trichodiene biosynthetic pathway. The interplay of balancing kinetics and thermodynamics in carbocation cyclization cascades has been discussed for this and other terpenoid synthases.^{2, 16}

The fact that the initial folding of the substrate in terpene synthases is crucial is well known,³⁸ as is discussed in our work on TDS.² Clearly, without the correct initial fold, the enzyme is unlikely to form the correct product. One may wonder why the same methodology at the same level of theory using M06-2X/6-31G(d)³⁹ in both studies yielded such vastly different qualitative and quantitative pictures on the carbocation cyclization cascade by TDS. In Ref. ² the barrier from the key intermediate bisabolyl cation 3 is just about 1 kcal/mol leading all the way to cation 6 (D in Ref. ¹), whereas, in Ref. ¹ there are multiple barriers as large as 11.8 and 10.8 kcal/mol for the same conversion. We have addressed the potential biological consequences of this difference, but from a computational perspective, a possible reason for this difference, if all simulations were performed correctly, is that the protein environment, e.g. the fold of the FPP substrate and its subsequent cation intermediates, is different. Since we identified a protein-substrate conformational state that yields a lower free energy barrier pathway, there is no conceivable reason to think that the real biological system (i.e. TDS) would chose a reaction pathway with multiple barriers that are more than 10 kcal/mol higher in energy to perform multiple reaction steps involving highly reactive intermediates. Hence, we disagree with the assertion by the authors of Ref. ¹ that the regio- and stereochemistry of terpenoid synthases is determined only by the FPP conformation and the selective activation of the initial farnesyl-phosphate bond, whereas the enzyme environment plays little role in regulating the subsequent carbocation cyclization processes. The selection of the FPP fold based on the initial farnesyl-phosphate bond cleavage in the work of Ref. ¹ certainly did not produce the correct intermediates and final product in TDS.