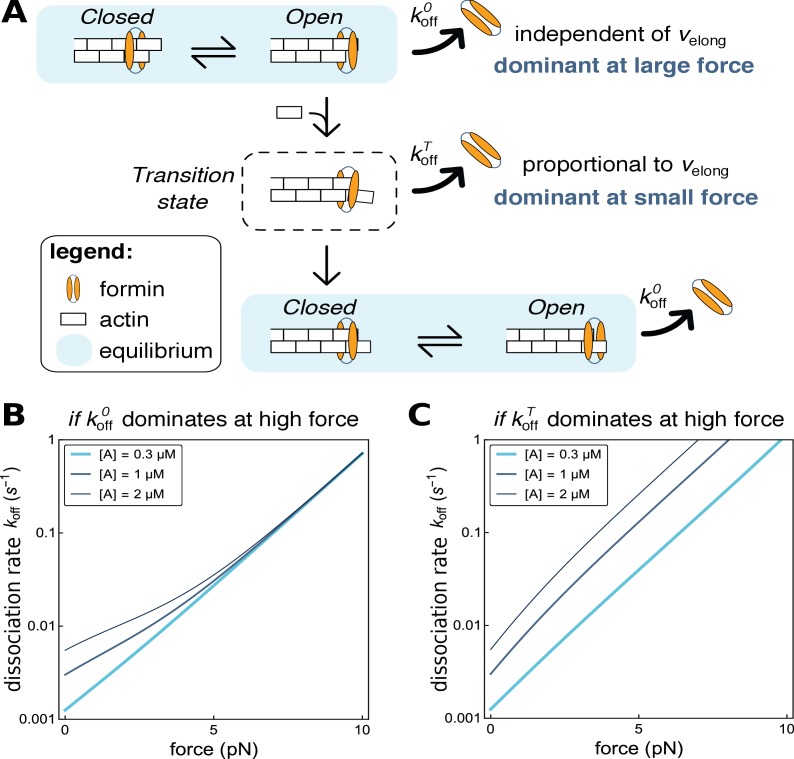
Figure 6. Modeling formin dissociation, in the absence of profilin.

(A) Sketch summarizing the conformations adopted by the FH2 dimer and the actin filament barbed end in our model, in the absence of profilin (for a complete description of the model, see Appendix 1). The system is in rapid equilibrium between an open and a closed state (depicted here as in the ‘stair-stepping’ model) and only the open state allows the addition of a new actin subunit at the barbed end. Following this elongation event, the system is in a transition state, which decays rapidly into a new open-closed rapid equilibrium. Formin dissociation from the barbed end can occur while the system is in the open state (with rate k_off^O) or in the transition state (rate k_off^T). The global, observable dissociation rate k_off comprises these two routes. (B,C) Predictions of the model for the variation of the dissociation rate k_off as a function of force, in log-linear representations. In both cases, k_off^T is the dominant contribution at zero force. In B, k_off^O increases more strongly than k_off^T when force is applied and thus becomes dominant at high force (computed with working distances δ_O=δ and δ_T=0, see Appendix 1). In C, k_off^T increases more strongly than k_off^O when force is applied (δ_O=0 and δ_T=δ, see Appendix 1).