Figure 5.

Low-Dimensional Bump Kinetics Explain Noise Variability in the Ring SSN

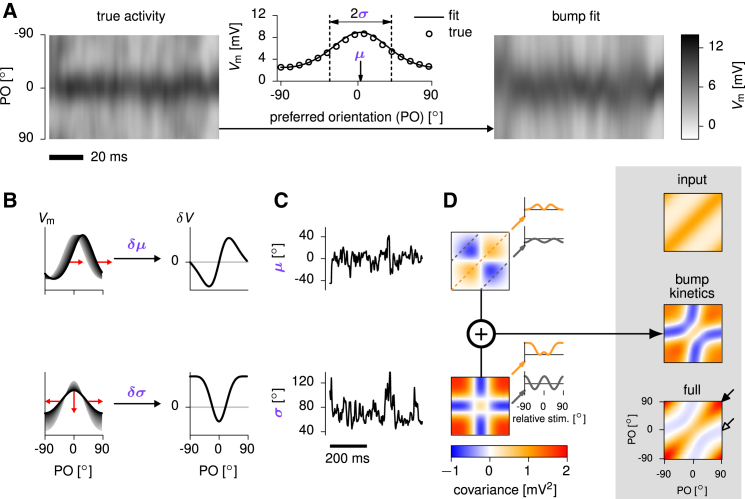
(A) Sample of $V_{\text{m}}$ fluctuations across the network in the evoked condition (left, “true activity,” 100% contrast), to which we fitted a circular-Gaussian function (bump) $V_i\left(t\right)=a\left(t\right)\text{exp}\left[\left(cos\left({\theta }_i-\mu \left(t\right)\right)-1\right)/{\sigma }^2\left(t\right)\right]$ across the excitatory population in each time step (center), parametrized by its location, μ, and width, σ. The amplitude of the bump, a, was chosen in each time step so as to keep total population firing rate constant. Fluctuations in location and width were independent, and the fit captured $87\text{\%}$ of the variability in $V_{\text{m}}$ (right).

(B) The two principal modes of bump kinetics: small changes (red arrows) in location (top) and width (bottom) of the activity bump result in the hill of network activity deviating from the prototypical bump (gray shadings). Plots on the right show how the activity of each neuron changes due to these modes of bump kinetics.

(C) Time series of μ and σ extracted from the fit.

(D) Ongoing fluctuations in each bump parameter contribute a template matrix of $V_{\text{m}}$ covariances (color maps show covariances between cells with preferred orientation [PO] indicated on the axes of the “full” matrix, bottom right), obtained from (the outer product of) the differential patterns on the right of (B). Insets show $V_{\text{m}}$ covariance implied by each template for pairs of identically tuned cells (orange, PO difference $\simeq 0^{\circ }$) and orthogonally tuned cells (gray, PO difference $={90}^{\circ }$), as a function of stimulus orientation relative to the average PO of the two cells. The two templates sum up to a total covariance matrix (“bump kinetics”), which captures the key qualitative features of the full $V_{\text{m}}$ covariance matrix (“full”). The covariance matrix of the input noise (“input”) is also shown above for reference. The stimulus is at $0^{\circ }$ throughout.