Nanobomb optical coherence elastography

Abstract

Wave-based optical elastography is rapidly emerging as a powerful technique for quantifying tissue biomechanical properties due to its noninvasive nature and high displacement sensitivity. However, current approaches are limited in their ability to produce high frequency waves and highly localized mechanical stress. In this work, we demonstrate that the rapid liquid-to-gas phase transition of dye-loaded perfluorocarbon nanodroplets (“nanobombs”) initiated by a pulsed laser can produce highly localized, high frequency, and broadband elastic waves. The waves were detected by an ultra-fast line-field low-coherence holography system. For comparison, we also excited waves using a focused micro air-pulse. Results from tissue-mimicking phantoms showed that the nanobombs produced elastic waves with frequencies up to ~9 kHz, which was much greater than the ~2 kHz waves excited by the air-pulse. Consequently, the nanobombs enabled more accurate quantification of sample viscoelasticity. Combined with their potential for functionalization, the nanobombs show promise for accurate and highly specific noncontact all-optical elastography.

The biomechanical properties of tissues can be significantly altered by various pathologies such as cancer [1]. Since elastography was formalized in the 1990s [2], there has been a massive growth in the interest of tissue biomechanical properties and their association with tissue pathologies. Traditional elastography techniques such as ultrasound elastography and magnetic resonance elastography have become powerful clinical techniques for detecting tissue elasticity changes from various diseases, such as breast cancer [3]. However, their limited spatial resolution, relatively poor displacement sensitivity, and contact-based excitation restrict their applications. Optical elastography techniques can overcome these limitations with superior spatial resolution and displacement sensitivity with the additional benefits of noninvasive excitation and imaging [4].

As with any elastography technique, optical elastography techniques generally rely on static/quasi-static or dynamic loading methods to induce tissue deformation and an associated imaging modality to sense these displacements. Initial investigations, such as with optical coherence tomography based elastography, primarily utilized compressional loading that provided high-resolution strain maps [5]. Mechanical compression is profoundly useful for applications where contact is not an issue, such as with skin and biopsy samples [6], but knowledge of the applied force is necessary to quantify the elasticity. Dynamic wave-based excitation is a promising alternative stimulation method that does not require knowledge of the excitation forces. However, many assumptions, such as tissue isotropy, biomechanical homogeneity, tissue geometry, and density homogeneity, are still utilized in the majority of investigations [7]. Nevertheless, noncontact wave excitation has been accomplished with various methods, such as a focused micro air-pulse [8] and acoustic micro-tapping [9]. While the air-pulse has been utilized in numerous studies, it cannot generate elastic waves with high frequencies as compared to acoustic micro-tapping (4 kHz). High frequency waves are particularly desired because they are less sensitive to tissue boundary conditions and geometry [10, 11] and low frequency waves limit elastographic spatial resolution due to their long wavelengths. To increase the frequency response of the elastic wave, Li et al. proposed excitation using a 532 nm pulsed laser that generated elastic waves with frequency content up to 12k Hz in murine skin [12]. To minimize any potential damage to the skin, a thin layer of agar was used as a shield.

In addition to various methods of wave generation, precise 3D spatial control of the mechanical excitation and specific tissue targeting has also been demonstrated to further enhance the utility of elastographic imaging. One such implementation is magnetomotive OCT (MM-OCT), which has been demonstrated in vivo using functionalized magnetic nanoparticles [13]. Ahmad et al. utilized the magnetic nanoparticles to generate elastic waves in rat liver [14]. However, the frequency content was still limited to approximately 1 kHz. In this work, we exploit the unique properties of dye-loaded perfluorocarbon (PFC) droplets to induce high frequency and broadband elastic waves. In addition, the lipid droplets can be functionalized, showing the potential for biocompatible functionalization [15].

Previous work has shown that the illumination of PFC nanodroplets loaded with light absorbing nanoparticles, e.g. gold or chromophores, with a nanosecond pulsed laser generated a strong photoacoustic signal [16]. The fundamental mechanism of this phenomenon is based on a rapid transient temperature increase inside the nanodroplets caused by the embedded chromophores absorbing the incident laser energy that results in the PFC droplet transitioning to a gas bubble. This process is associated with a very fast and localized volume expansion that induces a highly localized mechanical stress. Furthermore, PFC agents have already been approved by the FDA for safe use in intravenous applications (e.g. CS-1000, Celsense Inc., PA, USA). However, the droplets have not yet been explored as a method to generate elastic waves for subsequent biomechanical assessment.

In this Letter, we introduce a new optical elastography technique that utilizes the rapid and localized vaporization of PFC droplets laden with light absorbing dye molecules. Because the PFC droplets produce a very fast mechanical expansion and can be produced with sizes of few hundred nanometers, we have termed them “nanobombs”. The nanobomb-induced elastic waves were detected using an ultra-fast line-field low coherent holography (LF-LCH) system. The ultra-fast line rate, high displacement sensitivity, and single-shot detection are particularly well suited for detecting nanobomb-induced elastic waves [17]. A pulsed laser was combined with the LF-LCH system to image the elastic waves generated by nanobombs in tissue-mimicking agar phantoms. For comparison with another noncontact excitation modality, we performed similar measurements using our previously developed focused micro air-pulse excitation [8]. The “gold standard” of uniaxial mechanical compressional testing (Model 5943, Instron Corp.) was used for validation the elastographic measurements. The viscoelasticity of phantoms was quantified by fitting the elastic wave dispersion to a Rayleigh wave model (RWM) [18]. Our results show a fundamental advantage of the nanobombs because they can generate very broad and high frequency elastic waves. In addition, the highly localized liquid-to-gas transition of the nanobombs, biocompatibility, and potential functionalization opens a new avenue for specific and robust noncontact all-optical elastography.

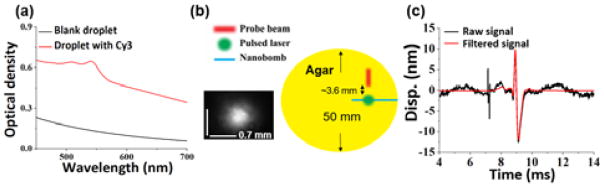
The nanobombs were prepared using dodecafluoropentane nanodroplets loaded with Cyanine 3 dye for optical excitation with a 532 nm pulsed laser. The nanodroplets were stabilized in water suspension inside the lipid micelles and were predominantly 487 ± 83.8 nm in diameter. The average diameter of the droplets was measured by dynamic light scattering (Delsa Nano C, Beckman Coulter, Inc.). Presence of the dye was further confirmed by absorbance spectra measurements, as shown in Fig. 1(a). The nanobombs were coated with lipids to ensure colloidal stability in an aqueous solution. Briefly, 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC, Avanti Polar Lipids, Inc.), 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-methoxy-polyethyleneglycol-2000 (DSPE-PEG-2000, Avanti Polar Lipids, Inc.), and cholesterol (Avanti Polar Lipids, Inc.) were dissolved at a weight ratio of 90:8.5:1.5, respectively, and a total weight of 20 mg was dissolved in 2 mL of chloroform. This mixture was added to a rotary evaporator (Cole-Palmer Instrument Company, LLC.), followed by formation of a lipid cake at 40°C. After the lipid cake was formed, 2 mL of deionized water was added to the lipid cake, and the suspension was placed on ice and was shaken at 150 rpm for 30 minutes. In parallel, 1 mg of powdered Cy3 dye (Lumiprobe Corp.) and 100 μL of 1% (v/v) aqueous solution of 1H,1H,2H-Perfluoro-1-hexene,3,3,4,4,5,5,6,6,6-Nonafluoro-1-hexene (Zonyl PFBE, Sigma-Aldrich Corp.) were added to 200 μL of dodecafluoropentane (FluoroMed L.P.), and the mixture was sonicated for 1 minute. Then, 2 mL of rehydrated phospholipids were added to the mixture of PFC, dye, and Zonyl PFBE, and the suspension was vortexed for 10 seconds followed by sonication for 15 minutes. The suspension was then centrifuged at 1000g for 5 minutes. The supernatant with free Cy3 dye was removed, and the lipid coated PFC droplets laden with the dye were re-suspended in 1 mL of deionized water.

Fig 1.

(a) Absorbance spectra of the PFC droplets without (blue) and with (red) embedded Cy3 dye. (b) Top-view of the phantom setup. (c) Displacement profiles before and after band-pass filtering.

The line field-low coherent holography (LF-LCH) system has been described in our previous work [17]. Briefly, low coherence infrared light (Broadlighter T-870-HP, SuperLum) was expanded to a line beam. The line focus at the camera image plane was ~5.2 μm in height. The useful beam sizes for the elastic wave propagation analysis were 0.50 mm and 1.45 mm for the nanobomb and air-pulse excitation experiments, respectively. The line beam illuminated ~350 CCD pixels, and the line rate was 100 kHz. The phase noise in a 1% agar phantom over 15 ms was 1 nm.

A frequency doubled Nd:YAG laser at 532 nm (Polaris II, New Wave Research, Inc.) was used to excite the nanobombs. Each pulse had an energy of 10 mJ and a 6 ns duration. The laser pulses were focused on the sample surface with an incidence angle of ~15° and a diameter of ~0.7 mm as shown in the lower left inset in Fig. 1 (b). The excitation and measurement of the elastic waves is also shown in Fig. 1 (b), where the excitation spot and LF-LCH beam were offset by ~3.6 mm. The air-pulse and pulsed laser were synchronized with the LF-LCH system for elastic wave detection.

Agar phantoms (Difco nutrient agar, Becton Dickinson) of two different concentrations (1% and 2%) were cast with a diameter of 50 mm and thickness of 10 mm (N=3 of each concentration). While reconstructing the phantom viscoelasticity with the RWM, the material density and Poisson ratio were set at 1000 kg/m³ and 0.49, respectively. In a typical experiment, 60 μL of a nanobomb suspension was injected into a 0.7 mm diameter channel approximately 0.5 mm below the surface of the phantoms using a syringe. Measurements were then performed either with the pulsed laser or the focused micro air-pulse [8].

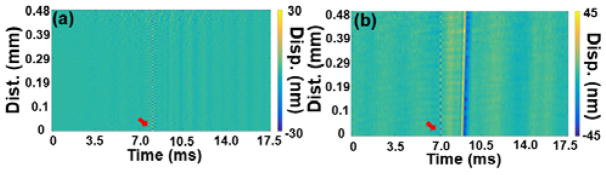
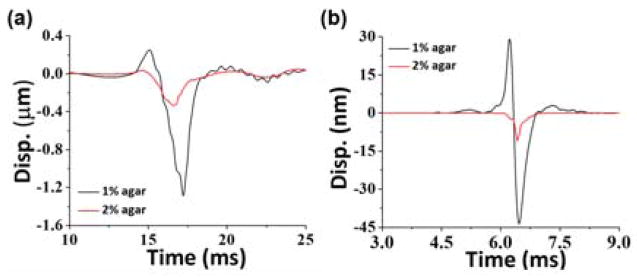
Displacement profiles of elastic waves were extracted by a Hilbert-based analytic method [17]. The measurements were taken 3.6 mm away from the excitation corresponding to 0 mm position in the spatio-temporal map. Low frequency motion below 500 Hz and the pulsed laser reflection were filtered as shown in Fig. 1(c). Validation experiments were performed on a homogeneous 1% agar phantom without nanobombs, and no elastic waves were observed after the pulsed laser excitation, as seen in Fig. 2(a). Once the nanobombs were injected, elastic waves were then detected. The resulting spatio-temporal map in Fig. 2(b) shows an obvious inclined strip corresponding to the nanobomb-induced elastic wave. These results demonstrated the feasibility of detecting nanobomb-induced elastic waves using the LF-LCH system. The temporal displacement profiles plotted in Fig. 3 show that nanobomb excitation induced waves with a much shorter temporal width than air-pulse excitation, which corresponds to higher frequencies.

Fig 2.

Spatio-temporal map of a 1% agar phantom without (a) and (b) with nanobombs. The red arrow indicates the pulsed laser reflection.

Fig. 3.

Elastic wave stationary temporal displacement profiles in agar phantoms induced by (a) air-pulse and (b) nanobomb.

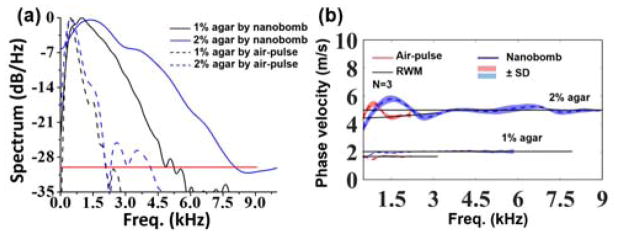
To quantify the excitation frequency response, fast Fourier transforms (FFTs) were performed on the temporal displacement profiles nearest to the excitation point, and the resulting power spectra are plotted in Fig. 4(a). The upper spectral limits of nanobomb-excited waves were at ~5 kHz and 9 kHz in 1% and 2% agars, respectively, using a cut-off threshold of −30 dB to minimize the influence of spectral dispersion and elastic wave attenuation on the velocity calculations [19]. In contrast, air-pulse excitation only yielded a maximum frequency of ~2 kHz at both concentrations of agar phantoms. Thus, the upper frequency of the nanobomb-excited wave in the 2% agar phantoms was 1.8 times greater than in the 1% agar samples, while there was no obvious difference between the samples with air-pulse induced waves. Ambroziński et al. reported that the center frequency of ultrasound induced elastic waves in a porcine cornea was shifted to a higher frequency when the corneal stiffness was increased [9], which corroborates with the frequency shift in the nanobomb-generated waves. Moreover, the nanobomb-excited elastic waves had a much wider bandwidth, as compared to the air-pulse induced waves, which enables more robust viscoelastic quantification by fitting to an analytical wave model (in this case, the RWM). Furthermore, higher frequencies are less susceptible to boundary conditions [10]. Both factors contribute to a more accurate quantification of sample viscoelasticity.

Fig 4.

(a) Averaged power spectra of the elastic waves excited by (dashed lines) air-pulse and (solid lines) nanobombs in (black) 1% and (blue) 2% agar phantoms. (b) Averaged elastic wave dispersion curves and fitting to the analytical RWM (N=3 for each). The shaded areas represent two standard deviations.

The elastic wave spectral dispersion was calculated by performing FFTs on the temporal displacement profiles. The phase shifts at each spatial position for a given frequency were then linearly fitted to the corresponding phase shifts [20]. Fits with R² < 0.85 were discarded to ensure high quality calculations. Due to the limited elastic wave frequencies induced by air-pulse excitation, the LF-LCH beam size was expanded to 2.20 mm to capture sufficient elastic wave propagation phase delays. The smaller beam enabled by the high frequency bandwidth of the nanobomb method has additional benefits of potential miniaturization of the LF-LCH system. The resulting elastic wave dispersion curves were fitted to the RWM to quantify the sample viscoelasticity [18].

Averaged dispersion curves from three samples per each agar concertation are presented in Fig. 4(b). The phase velocities below 500 Hz were removed due to system noise and bulk motion from samples. The dispersion curve of the nanobomb excited elastic wave flattened at 3.5 kHz for 2% agar (wavelength: ~1.4 mm) but at 1 kHz for 1% agar (wavelength: ~2 mm) due to a slower propagation speed of the elastic wave in the softer 1% agar. The wave appeared to converge to a Rayleigh wave when the wavelength was less than 2 mm or about 1/5 the height of the phantoms. For RWM quantification, the fitting ranges for 1% agar phantoms were from 1 kHz to 2 kHz for the air-pulse induced waves and 1 kHz to 6 kHz for the nanobomb-induced waves. For the 2% agar phantoms, the fitting range was from 1 kHz to 2.2 kHz for the air-pulse measurements and 3.5 kHz to 9 kHz for the nanobomb measurements. We suspect that the curved regions at the lower frequencies are primarily due to the sample boundary conditions [10]. Further investigation of the elastic wave behavior at low frequencies is an avenue of future work.

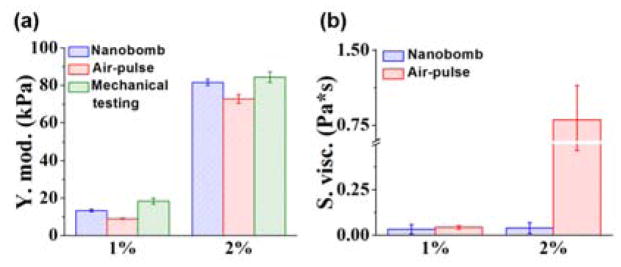
Agar is a non-dispersive media [21, 22], so any observed dispersion is due to extraneous factors that are not representative of the intrinsic material properties of agar. The flat dispersion at higher frequencies in the agar samples, as plotted in Fig. 4(b), shows that shorter wavelengths are less influenced by a sample thickness. The dispersion of elastic waves excited by nanobombs and by air-pulse in the 1% agar phantoms flattened to ~2 m/s and ~1.7 m/s, respectively. However, the air-pulse induced elastic wave dispersion curve in 2% phantoms did not flatten, which is likely due to the limited frequency content of the air-pulse induced elastic wave. The Young’s moduli and shear viscosities estimated by the RWM are plotted in Figure 5(a). The elasticity of 1% agar phantoms was estimated as 13.2 ± 0.6 kPa by nanobomb excitation and 9.0 ± 0.2 kPa with air-pulse stimulation. Mechanical testing measured the stiffness of the 1% agar phantoms as 18.3 ± 1.5 kPa. The Young’s modulus of 2% agar phantoms was estimated as 81.6 ± 1.7 kPa and 72.7 ± 2.3 kPa by nanobomb and air-pulse excitation, respectively. The elasticity of the 2% agar phantoms was measured as 84.3 ± 2.8 kPa by mechanical testing. These results are consistent with our previous work [23]. The shear viscosity of 1% agar samples was estimated as 0.03 ± 0.02 Pa·s by nanobomb excitation and 0.04 ± 0.01 Pa·s by air-pulse stimulation. The shear viscosity of 2% agar samples was estimated as 0.04 ± 0.03 Pa·s and 0.80 ± 0.34 Pa·s by nanobomb and air-pulse stimulation, respectively. As mentioned earlier, agar is nondispersive, so we expect low values for viscosity [14]. However, air-pulse excitation resulted in a significant overestimation of viscosity due to insufficient frequency content of the elastic wave. Overall, the nanobomb excitation enabled a more accurate quantification of sample viscoelasticity and is better suited for thin and/or stiff samples than the focused air-pulse due to the extended bandwidth and high frequency content that is less susceptible to boundary conditions.

Fig 5.

(a) Young’s moduli and (b) shear viscosity of phantoms quantified by the RWM. The error bars represent standard deviation (N=3 of each concentration).

However, there are several challenges that need to be addressed prior to in vivo application of the nanobombs. The pulsed laser fluence (2.5 J/cm²) was above maximum permissible exposure for skin (0.2 J/cm²), and the excitation wavelength (532 nm) has limited penetration depth in tissue. To resolve these challenges, the nanobombs will be further refined to require less incident energy for elastic wave generation. In addition, excitation at 1064 nm can improve penetration depth up to 1 mm [24]. Although we injected the nanoparticles into a channel, lipid nanoparticles have been functionalized for targeted applications [15]. In addition, we are currently developing smaller nanobombs and decreasing the excitation spot size to increase the upper bound of frequencies in the elastic wave and to improve resolution of OCE [25]. Developing more efficient, biocompatible, and functionalized nanoparticles along with minimally invasive delivery is the next step of our work.

In summary, our work demonstrates a novel application of dye-loaded PFC nanodroplets (“nanobombs”) for inducing high frequency and broadband elastic waves noninvasively using optical excitation. The ultra-fast LF-LCH system enables single shot detection of these waves with a sufficient sampling rate. In comparison to a focused micro air-pulse, the nanobombs produced higher frequency waves with wider bandwidths. Our results open a new avenue for development of an optical elastography method where nanobombs can produce a rapid, highly localized, and targeted mechanical stress.