A regression framework for assessing covariate effects on the reproducibility of high-throughput experiments

Summary

The outcome of high-throughput biological experiments is affected by many operational factors in the experimental and data-analytical procedures. Understanding how these factors affect the reproducibility of the outcome is critical for establishing workflows that produce replicable discoveries.

In this work, we propose a regression framework, based on a novel cumulative link model, to assess the covariate effects of operational factors on the reproducibility of findings from high-throughput experiments. In contrast to existing graphical approaches, our method allows one to succinctly characterize the simultaneous and independent effects of covariates on reproducibility and to compare reproducibility while controlling for potential confounding variables. We also establish a connection between our model and certain Archimedean copula models. This connection not only offers our regression framework an interpretation in copula models, but also provides guidance on choosing the functional forms of the regression. Furthermore, it also opens a new way to interpret and utilize these copulas in the context of reproducibility.

Using simulations, we show that our method produces calibrated type I error and is more powerful in detecting difference in reproducibility than existing measures of agreement. We illustrate the usefulness of our method using a ChIP-seq study and a microarray study.

1. Introduction

High-throughput technologies are indispensable tools in modern biological research. In each experiment, a large number of candidates are evaluated for their association with a biological feature of interest, and the ones with significant associations are identified for further analyses. Despite their widespread use, outputs from high-throughput experiments are quite noisy and the reliability of their findings is a constant concern. Because ground truth is usually lacking in this type of studies, the reproducibility of outcomes across replicated experiments plays an important role in establishing confidence in measurements and evaluating the performance of a workflow.

The performance of a high-throughput workflow can be affected by many operational factors, for example, experimental platforms or protocols, parameter settings in experimental procedures or data-analytical procedures, and labs conducting the experiments. Understanding how these factors affect the reproducibility of the outcome is crucial for identifying potential sources of irreproducibility and designing workflows that produce reliable results.

An important criterion for assessing the reproducibility of high-throughput experiments is how consistently significant candidates are ranked in replicate experiments. If the significance threshold is set, this assessment is straightforward: one may first identify the candidates that pass the threshold on individual replicates, then evaluate the reproducibility of the identifications, by computing, for example, the (rank) correlation between the significance scores of common identifications or the proportion of candidates that are commonly identified on the replicates. However, this evaluation depends on the choice of the threshold, thus may not truly reflect the intrinsic reproducibility of the workflows being evaluated.

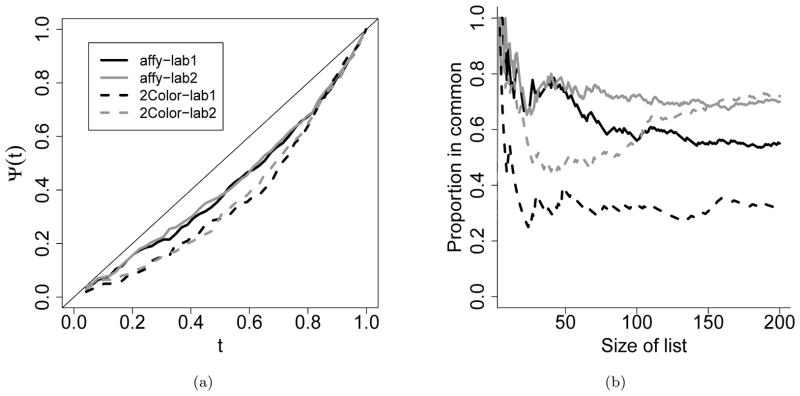
A natural remedy is to perform the evaluation sequentially at a series of thresholds, and then to use the entire profile to describe the reproducibility of a workflow. By comparing the profiles, the reproducibilities of different workflows can be assessed, without linking them to any specific significance thresholds. This is particularly useful when the significance scores from different workflows are on different scales. Several graphical tools have been developed based on this sequential approach, for example, the correspondence at the top (CAT) plot (Irizarry et al., 2005) and the correspondence curve (Li et al., 2011). These tools have been used in various high-throughput settings for evaluating the inter and intra-platform reproducibility of microarray (Irizarry et al., 2005; Guo et al., 2006), cross-platform correspondence between microarray and RNA-seq (Kim et al., 2011), and the reproducibility of ChIP-seq studies (Landt et al., 2012; Li et al., 2011).

However, these tools are inconvenient to use for assessing the effects of operational factors on reproducibility, because they do not provide any quantitative summaries or statistical inference. For example, in a multiple-laboratory microarray study, Irizarry et al. (2005) studied how lab and platform affect the reproducibility of differential gene expression levels between a pair of replicate samples (details in Section 5). To investigate the lab and platform effects, identical biological samples were provided to all the labs, and the gene expression levels were measured by each lab on at least one of the three microarray platforms. Table 5a shows the measurements for a subset of genes. For each lab-platform combination, a CAT curve was plotted to evaluate the concordance between the absolute log2 fold changes across the replicates. The curves then were compared to assess platform and lab differences (Figure 1b for a subset of four combinations). Though these curves are useful for visual comparison, lab or platform effects are difficult to infer due to lack of statistical inference. The comparison also becomes visually challenging when there are more than a handful of curves (cf. Figure 2b in Irizarry et al. (2005) for ten combinations). Moreover, for some experimental designs, e.g. incomplete designs, it is impossible to plot curves for all the combinations, as observations from some combinations of operational factors are not available. In these scenarios, succinct numerical summaries on the effects of operational factors and their statistical inference are more useful for drawing scientific conclusions.

Table 5.

Application on a multiple-lab multiple-platform microarray study (Irizarry et al., 2005).

(a) Absolute log2 fold change of a subset of 200 most differentially expressed genes.
	workflow 1 (affy-lab1)		workflow 2 (affy-lab2)		workflow 3 (2-color-lab1)		workflow 4 (2-color-lab2)
gene	rep1	rep2	rep1	rep2	rep1	rep2	rep1	rep2
1	4.034	4.484	4.328	4.647	3.583	3.721	6.028	6.004
…	…	…	…	…	…	…	…	…
100	0.984	0.666	0.989	0.804	1.949	0.944	1.933	1.764
…	…	…	…	…	…	…	…	…
200	0.748	0.372	0.755	0.766	1.723	1.057	1.469	1.546

(b) Lab and platform effects on the reproducibility of differentially expressed genes across a pair of replicate samples.
		Estimate	95% confidence interval
Baseline	α1	−0.548	[−0.760, −0.335]
	α2	0.970	[0.913, 1.028]
Two-color oligo	βP	−0.274	[−0.514, −0.034]
Lab 2	βL	0.034	[−0.206, 0.273]

Figure 1.

The correspondence curve and the CAT plot illustrated using a microarray dataset in Irizarry et al. (2005). Plotted is the most differentially expressed 200 genes measured on the Affymetrix and two-color oligo platforms in Labs 1 and 2. (a) The correspondence curve. (b) The correspondence-at-the-top (CAT) plot.

In this work, we develop a regression framework, motivated from the correspondence curve (Li et al., 2011), to assess how operational factors affect the reproducibility of high-throughput experiments. The key idea is to view the correspondence curve as a series of probabilities that a candidate is reproducibly identified at a sequence of thresholds, and then model its relationship with operational factors through a novel cumulative link model. Using this formulation, our model not only incorporates the sequential feature of the aforementioned graphical tools, but also provides the power and flexibility associated with regression models.

Moreover, we also establish a connection between this model and certain Archimedean copula families through an algebraic relationship. Archimedean copulas are a class of parametric copulas. They are widely used to model dependence structures in multivariate data, especially in actuarial science, finance, hydrology, and survival analysis (see Genest and Favre (2007) for a review). The connection that we establish allows the regression coefficients in our model to be interpreted in copula models, naturally linking reproducibility with classical multivariate dependence models. Importantly, this connection provides a principled approach to selecting the canonical form of our regression model, analogous to the selection of canonical link functions in the generalized linear models (GLM). It also opens a new way to interpret and utilize these copulas in the context of reproducibility of high-throughput biological experiments.

The remainder of the article is organized as follows. In Section 2, we present our regression framework. We first describe a key interpretation of the correspondence curve that motivates the development of our method, then present our regression model, its connection with Archemidean copulas, and its interpretation as a cumulative link model. Section 3 presents the estimation procedure. In Section 4, we use simulation studies to evaluate the performance of our method. In Section 5, we apply our method to two real datasets that motivated this study. Section 6 discusses future work and enhancement.

2. Methods

The data that we consider consist of outputs of high-throughput experiments generated from S workflows (S ≥ 2). All the workflows measure the same underlying biological process, but they differ in certain operational factors, for example, experimental protocols, measurement platforms, or experimental parameters. Denote the vector of operational factors for the workflow s as x^s. For each workflow, few replicates are available, such that the reproducibility of the findings identified in the workflow can be assessed across replicates. Table 5a shows an example with four workflows, two replicates and two factors. We will focus on the case of two replicates, as this is the primary focus of most existing methods, including the aforementioned graphical tools and correlation measures. For each replicate, the output consists of a list of candidates, such as genes or protein-binding sites, and their significance scores, which are assigned by the workflow to indicate the strength of evidence for a candidate to be a true signal. The scores can be original measurements (e.g. fold enrichment) or test statistics derived from original measurements (e.g. p-value). They can distribute differently on different replicates. We will use the scores as our data. Without loss of generality, we assume that a score of small value indicates strong evidence (e.g. p-value) and receives a low value in its rank, i.e. the most significant candidate receives rank one. For scoring systems that represent strong evidence using high values, a monotonic transformation can be applied to reverse the order. Our interest is to quantitatively evaluate how operational factors affect the reproducibility of the rank lists across replicates.

Let ${\mathbf{Y}}_1^s=(Y_{1,1}^s,Y_{1,2}^s),\dots ,{\mathbf{Y}}_n^s=(Y_{n,1}^s,Y_{n,2}^s)$ be the significance scores of a sample of n candidates on two replicates, assigned by the workflow s. We suppose that the scores $Y_{1,j}^s,\dots ,Y_{n,j}^s$ on the replicate j = 1, 2, are a sample of the random variable $Y_j^s$ from an unknown distribution $F_j^s$. Because scores from different replicates may be on different scales, we identify significant candidates by the ranks of their scores, rather than the actual values. That is, given a cutoff t ∈ (0, 1), a candidate i is deemed as significant on the jth replicate, if its score $Y_{i,j}^s\le {\mathbb{F}}_j^{s-1}(t)$, where ${\mathbb{F}}_j^s(·)$ is the empirical version of $F_j^s(·)$, and ${\mathbb{F}}_j^{s-1}(·)$ is the inverse of ${\mathbb{F}}_j^s(·)$. We declare a candidate as a reproducible identification from the workflow s, if it is significant on both replicates, i.e. $Y_{i,1}^s\le {\mathbb{F}}_1^{s-1}(t)$ and $Y_{i,2}^s\le {\mathbb{F}}_2^{s-1}(t)$. For notational simplicity, we omit the superscript s when no confusion arises thereinafter.

2.1 Probabilistic interpretation of the correspondence curve

To motivate our method, we first provide a brief introduction to the correspondence curve (Li et al., 2011), in comparison with the CAT plot (Irizarry et al., 2005), and then describe a key interpretation of the correspondence curve that leads to the development of our regression model.

The correspondence curve is a graphical tool for visualizing how the concordance of two rank lists changes in the decreasing order of significance. Suppose n candidates are evaluated. Let 𝒯 = {t | 0 < t₁ < … < t_M ≤ 1} be a set of prespecified thresholds (M < n). The correspondence curve is constructed by plotting the pairs of (t,Ψ_n(t)) for all t ∈ 𝒯, where

$${\mathrm{\Psi }}_n(t)=\frac{1}{n}\sum _{i=1}^{n}I(Y_{i,1}\le {\mathbb{F}}_1^{-1}(t),Y_{i,2}\le {\mathbb{F}}_2^{-1}(t))$$

is the proportion of common entries that pass the threshold t among all candidates. This curve has characteristic shapes at independence (a parabola of Ψ_n(t) = t²) and at perfect positive correlation (a line of Ψ_n(t) = t). The strength of concordance between the rank lists and how the concordance changes with the significance can be read off from the curve by comparing the curve with the characteristic shapes. Its detailed properties can be found in (Li et al., 2011). Figure 1a shows the correspondence curves of four lab-platform combinations, computed using the absolute log2 fold change on two replicate samples, in the multiple-laboratory microarray study (Irizarry et al., 2005) in Section 5.

A closely related curve is the CAT plot (Irizarry et al., 2005). To construct a CAT plot, one makes a list of l most significant candidates for each rank list, and plots the proportion of common entries on the two lists against the list size l. If one rewrites l ≡ ⌈tn⌉, where ⌈tn⌉ is the smallest integer that is greater than tn, then this curve is equivalent to plotting the pairs of (t, ${\mathrm{\Psi }}_n^{\ast }(t)$) and rescaling the x-axis by n, where

$${\mathrm{\Psi }}_n^{\ast }(t)=\frac{1}{\lceil tn\rceil }\sum _{i=1}^{n}I(Y_{i,1}\le {\mathbb{F}}_1^{-1}(t),Y_{i,2}\le {\mathbb{F}}_2^{-1}(t)).$$

Figure 1b shows the CAT plots of the same data as in Figure 1a.

Though both Ψ_n(t) and ${\mathrm{\Psi }}_n^{\ast }(t)$ represent the proportion of common entries that pass a threshold t, Ψ_n(t) is with respect to all candidates, whereas ${\mathrm{\Psi }}_n^{\ast }(t)$ is with respect to candidates that pass the threshold on one replicate. This subtle difference makes Ψ_n(t) a nondecreasing function of t, but not ${\mathrm{\Psi }}_n^{\ast }(t)$. Consequently, the correspondence curve is nondecreasing with t, whereas the shape of a CAT plot can vary substantially with the spacing of t. As it is easier to model a nondecreasing curve, we will develop our model based on the correspondence curve.

Our key observation is that the population version of Ψ_n(t),

$$\mathrm{\Psi }(t)=E[I(Y_1\le F_1^{-1}(t),Y_2\le F_2^{-1}(t))]=P(Y_1\le F_1^{-1}(t),Y_2\le F_2^{-1}(t))$$ (1)

is the probability that a candidate is reproducibly identified on both replicates at a given threshold t. Hence, the correspondence curve can be viewed as a set of probabilities that a candidate is reproducibly identified at a series of thresholds. Note that $P(Y_j\le F_j^{-1}(t))=t$, so the threshold t actually is the probability that a candidate is identified on a single replicate. Therefore, the correspondence curve can be interpreted as an illustration of the empirical relationship between the probability of being reproducibly identified and the probability of being identified on individual replicates. A model-based approach depicting this relationship will be useful for succinctly summarizing the information provided by a correspondence curve. Furthermore, (1) indicates that each point on the correspondence curve can be interpreted as an expectation of a binary random variable, $V_{i,t}=I(Y_{i,1}\le {\mathbb{F}}_1^{-1}(t),Y_{i,2}\le {\mathbb{F}}_2^{-1}(t))$, at threshold t. This suggests that the inference on a correspondence curve can be based on V_i,t.

2.2 A regression model for a correspondence curve

We first consider a single correspondence curve. To model the curve, we take a parametric approach to represent the curve in a regression model, with Ψ(t) as the response variable and t as the predictor. As Ψ(t) can be interpreted as the expectation of the binary random variable V_i,t, we model this relationship using the generalized linear models (GLM) for binary responses. We therefore call this model the correspondence curve regression and define it as,

$$g(\mathrm{\Psi }(t))=\sum _{k=1}^K{\alpha }_k{h}_k(t),t\in \mathcal{T},$$ (2)

where 𝒯 = {t | 0 < t₁ < … < t_M ≤ 1} is a set of prespecified thresholds, g is a known link function, h = (h₁, …, h_K) are prespecified functions, and α = (α₁, …, α_K) is an unknown parameter vector that reflects how the probability of being reproducibly identified changes with the probability of being identified on a single replicate through h. Clearly, the more predictive t is to Ψ(t), the higher the reproducibility is. Thus the value of α_k reflects the strength of the reproducibility.

Note that Ψ(t) is by definition a monotonically increasing function of t, Ψ : [0, 1] → [0, 1]. Thus, g and h_k must be chosen in a way to ensure that $g^{-1}\left({\sum }_{k=1}^K{\alpha }_k{h}_k(t)\right)$ is a monotonically increasing function with respect to t, satisfying $g^{-1}\left({\sum }_{k=1}^K{\alpha }_k{h}_k(0)\right)=0$ and $g^{-1}\left({\sum }_{k=1}^K{\alpha }_k{h}_k(1)\right)=1$. For example, one simple choice is logit(Ψ(t)) = α₁+logit(t). In this form, α₁ represents the log odds ratio of being reproducibly identified over being identified on a single replicate. A larger α₁ reflects a higher reproducibility. In Section 2.3, we will describe a procedure to select the optimal choice of g, K, and h_k according to the empirical dependence structure of (Y₁, Y₂).

Remark 1

The cutoff set 𝒯 typically consists of evenly spaced cutoff points in the range of (0, 1]. In some applications, signals that fail to pass a critical value t₀ will be of no practical interest, then one may set t_M ≤ t₀. We will evaluate how spacing between cutoff points affects the accuracy of estimation using simulations in Section 4.

2.3 Selection of K, h_k and g through a connection with Archimedean copula models

Our model is essentially a parametric model to describe the relationship between the joint cumulative distribution function and the marginal cumulative distribution function for a bivariate distribution. One commonly used model for describing such a relationship is the copula model. As we will show, our regression model (2) is indeed related to Archimedean copulas. This connection not only offers our model and its regression coefficients an interpretation in the context of copula models, but also provides a principled way to select the functional form of our regression model.

Introduction to Archimedean copulas

We first give a brief introduction to Archimedean copulas and refer to (Joe, 1997; Nelsen, 2006) for details. Copulas are multivariate models for modeling the dependence of multiple random variables. A J-dimensional copula, C : [0, 1]^J → [0, 1], is the multivariate cumulative distribution function, C(t₁, …, t_J) = P(T₁ ≤ t₁, …, T_J ≤ t_J), of uniform random variables T₁, …, T_J. Archimedean copulas are a class of parametric copulas that can be written in the form of

$$\psi (C(t_1,\dots ,t_J);\theta )=\psi (t_1;\theta )+\dots +\psi (t_J;\theta ),$$ (3)

where θ is an association parameter describing the strength of the dependence between T_j’s, and ψ is a parametric function specific to each Archimedean copula, mapping [0, 1] into [0,∞), called a generator function. Archimedean copulas consist of a great variety of families of copulas and can model various dependence structures. A list of commonly-used Archimedean copulas and their properties can be found in Nelsen (2006).

Connection with Archimedean copula models

To establish the connection between our model and Archimedean copula models, note that, when J = 2, the response variable in our model is actually the diagonal section of a bivariate copula, i.e. Ψ(t) = C(t, t). If C is an Archimedean copula with a generator function Ψ and an association parameter θ, then by (3),

$$\psi (\mathrm{\Psi }(t))\equiv \psi (C(t,t);\theta )=2\psi (t;\theta ).$$ (4)

For certain ψ, we observe that, after some algebraic rearrangement, (4) can be represented in the form of

$$g(\mathrm{\Psi }(t))=\sum _{k=1}^K{\alpha }_k(\theta )h_k(t),$$ (5)

where h_k(·) is a function of t (free of θ) and α_k(θ) is a function of θ (free of t). For these copulas, their diagonal sections can be precisely represented in the form of our regression model (2), with the link function g and (h₁, …, h_K) as specified in (5). The value of K and the forms of h_k and g are determined by the generator function ψ. We therefore refer to these functions as the canonical functions for the corresponding copula. With the canonical functional form, α_k’s in (2) are functions of the association parameter θ in the corresponding copula model. Thus the estimates of α_k reflect the strength of association, naturally linking reproducibility with the association of (Y₁, Y₂).

To see how this works, we consider two simple examples.

Example 1

The Gumbel-Hougaard copula (Hougaard, 1986; Nelsen, 2006) is a 1-parameter Archimedean copula with the generator function, ψ(t) = (−log(t))^θ, where θ ∈ [1,∞). Based on (4), [−log(Ψ(t))]^θ = 2(−log(t))^θ. After simplification, we obtain log(Ψ(t)) = 2^1/θ log(t). It follows the regression form in (5), with g = log(·), K = 1, h₁ = log(·) and α₁ = 2^1/θ.

Example 2

The copula labeled as (4.2.12) in Table 4.1 in Nelsen (2006) (referred to as Nelsen 4.2.12 copula thereinafter) is a 1-parameter Archimedean copula with the generator function, $\psi (t)={(\frac{1}{t}-1)}^{\theta }$, where θ ∈ [1,∞). Based on (4), ${(\frac{1}{\mathrm{\Psi }(t)}-1)}^{\theta }=2{(\frac{1}{t}-1)}^{\theta }$. After simplification, we obtain $\text{logit}(\mathrm{\Psi }(t))=-\frac{log2}{\theta }+\text{logit}(t)$. It follows the regression form in (5), with g = logit(·), K = 2, h₁ = 1, h₂ = logit(·), ${\alpha }_1=-\frac{log2}{\theta }$ and α₂ = 1.

In Table 1, we identify a class of Archimedean copulas whose generator functions satisfy (4), and derive the corresponding g, α_k and h_k (details in Supplementary materials). Interestingly, we observe that g and h_k have the same basic functional form for each copula in this class. Thus the corresponding regression models can be viewed as representing the relationship between t and Ψ(t) in various transformations. Moreover, we observe that the canonical link functions g for these copulas take the form of log(·), logit or odds. Thus covariate effects can be easily interpreted, for example, as relative probability or odds ratio to report reproducibly.

Table 1.

Canonical choices of K, g and h_k(t) for Archimedean copulas that can be represented in the regression form of (5), i.e. $g(\mathrm{\Psi }(t))={\sum }_{k=1}^K{\alpha }_k(\theta )h_k(t)$. The last four copulas are labeled according to their indices in Table 4.1 in Nelsen (2006).

Name	K	g(Ψ(t))	hk(t)	αk
Ali-Mikhail-Haq	2	$\frac{1-\mathrm{\Psi }(t)}{\mathrm{\Psi }(t)}$	$h_1(t)=\frac{1-t}{t}$, h2(t) = h1(t)2	α1 = 2, α2 = (1 − θ)
Gumbel-Hougaard	1	log Ψ(t)	h1(t) = logt	α1 = 21/θ
Gumbel-Barnett	2	log Ψ(t)	h1(t) = logt, h2(t) = (h1(t))2	α1 = 2, α2 = −θ
(4.2.2) in Nelsen	1	1 − Ψ(t)	h1(t) = 1 − t	α1 = 21/θ
(4.2.7) in Nelsen	2	1 − Ψ(t)	h1(t) = 1 − t, h2(t) = h1(t)2	α1 = 2, α2 = −θ
(4.2.12) in Nelsen	2	$log\frac{\mathrm{\Psi }(t)}{1-\mathrm{\Psi }(t)}$	h1(t) = 1, $h_2(t)=log\frac{t}{1-t}$	${\alpha }_1=-\frac{log2}{\theta }$, α2 = 1
(4.2.18) in Nelsen	2	$\frac{1}{1-\mathrm{\Psi }(t)}$	h1(t) = 1, $h_2(t)=\frac{1}{1-t}$	${\alpha }_1=-\frac{log2}{\theta }$, α2 = 1

Remark 2

Note that α_k is free of t. This indicates that the relationship between Ψ(t) and h(t) is homogeneous throughout the entire range of t. We refer to this property as the homogeneous reproducibility property and this class of copulas as the homogeneous reproducibility class. As shown in Table 1, several commonly-used Archimedean copulas are in this class. To the best of our knowledge, this property and this class have not been reported in literature.

Selection of K, h_k and g

The connection above suggests a principled way to select the functional forms of h_k and g in our regression (2). That is, the selection of functional forms can be done by finding the suitable parametric copula model for the distribution of (Y₁, Y₂), which has been well studied (Embrechts, 2009). This is analogous to the selection of the canonical link function for GLMs, which is also determined by the distribution of the response variable.

To proceed, one first selects the copula following the general guideline for copula selection (Genest and Favre, 2007), i.e. first plotting the rank scatterplot of the empirical distribution of (Y₁, Y₂), and then choosing a copula in Table 1 whose shape and tail behavior are similar to what is shown in the rank scatterplot. A formal goodness-of-fit test for copulas, such as Fermanian (2005); Genest et al. (2009), can be conducted to validate the choice. The regression form then can be found from Table 1 by looking up the copula.

Remark 3

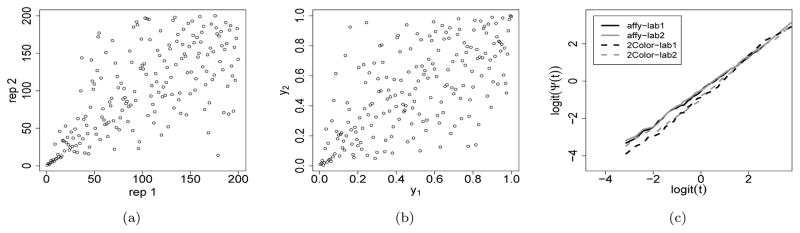
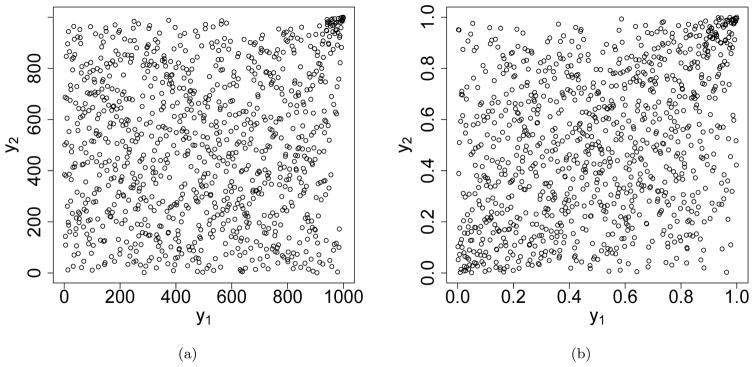
In high-throughput experiments, candidates relevant to the biological interest typically are ranked higher and have a much higher rank consistency across replicates than irrelevant ones. The rank scatterplot of the scores (or in their reversed order) often resembles the shapes and tail behaviors of the Nelsen 4.2.12 copula (Figure 3a–b) (or Gumbel-Hougaard copula (Figure 2)) to some extent. The regression model with the corresponding functional forms is likely to be a good fit.

Figure 3.

Graphical illustration of the most differentially expressed 200 genes from Labs 1 and 2 on the Affymetrix and two-color oligo platforms in Irizarry et al. (2005). (a) Rank scatterplot of the absolute log2 fold change for the 200 genes. (b) Density plot of the Nelsen 4.2.12 copula (θ = 1.5). (c) Exploratory data analysis shows an approximated linear trend between logit(t) and logit(Ψ(t)).

Figure 2.

(a) Rank scatterplot of the simulated data (n = 1000) in the high-throughput setting (ρ₁ = 0.6 and π = 0.05). (b) Density plot of a Gumbel-Hougaard copula (θ = 1.3).

Remark 4

It is worth noting that a regression model with the canonical form is not equivalent to the corresponding copula model, since it only specifies the diagonal section of the copula rather than the full parametric form. Therefore, the regression model is more robust to model violations in the off-diagonal region of the joint distribution of (Y₁, Y₂) than the full copula model. One may also choose other functional forms based on the empirical relationship between Ψ(t) and t. In this case, the regression model no longer corresponds to a known parametric copula.

2.4 Correspondence curve regression with covariates

Our goal is to assess the influence of operational factors on the reproducibility of workflows. Let x be a vector of d covariates corresponding to operational factors for a workflow. For categorical variables, x will be the associated vector of dummy variables. Then we can incorporate the operational factors as covariates in (2) as

$$g(\mathrm{\Psi }(t\mid \mathit{x}))=\sum _{k=1}^K{\alpha }_k{h}_k(t)+\mathit{W}{(t,\mathit{\beta })}^T\mathit{x},t\in \mathcal{T},$$ (6)

where $\mathrm{\Psi }(t\mid \mathit{x})=P(Y_1\le F_1^{-1}(t),Y_2\le F_2^{-1}(t)\mid \mathit{x})$, W(t, β)^Tx is a linear predictor characterizing the effect of the covariates x on reproducibility, and β = (β₁₁, …, β_1K, …, β_d1, …, β_dK)^T are unknown coefficients to be estimated. Here W(t, β) = (W₁(t, β₁), …, W_d(t, β_d))^T, with $W_p(t,{\mathit{\beta }}_p)={\sum }_{k=1}^K{\beta }_{pk}{h}_k(t)$, where (h₁, …, h_K) is the same set of functions as the one for the baseline terms, and β_pk measures the covariate effect on h_k(t) due to x_p for p = 1, …, d.

To fix ideas, we consider the simple regression model for the previous two examples.

Example 1 (Continued)

A simple regression model for the Gumbel-Hougaard copula. The canonical baseline regression is log(Ψ(t)) = α₁ log(t), where α₁ = 2^1/θ. The covariate term: W(t, β) = α_1,x=1 log(t) − α_1,x=0 log(t) ≡ β log(t). Then the corresponding simple regression model is log(Ψ(t)) = α₁ log(t) + β log(t)x. It indicates that the probability that a candidate is reproducibly ranked among top 100t% in X = 1 is t^β times of that in X = 0.

Example 2 (Continued)

A simple regression model for the Nelsen 4.2.12 copula. The canonical baseline regression is logit(Ψ(t)) = α₁ + logit(t), where ${\alpha }_1=-\frac{log2}{\theta }$. The covariate term: W(t, β) = α_1,x=1 + logit(t) − (α_1,x=0 + logit(t)) ≡ β. Then the corresponding simple regression model is logit(Ψ(t)) = α₁+logit(t)+βx. It indicates that the odds that a candidate is reproducibly ranked among top 100t% in X = 1 is exp(β) times of that in X = 0.

2.5 Connection to cumulative link models

To better understand our method, we compare it with the standard cumulative link model for modeling ordinal data (McCullagh, 1980),

$$g(P(Y\le c_m\mid \mathit{x}))={\alpha }_m^{\ast }+{\mathit{\beta }}^T\mathit{x},$$ (7)

where g is a link function, (c₁, …, c_M) are cutoff points, ${\alpha }_m^{\ast }$ is the intecept reflecting the effect of cutoff c_m at baseline, and β are regression coefficients. Our model (6) is similar to (7) in that both models dichotomize responses according to a series of thresholds and evaluate the covariate effects using a cumulative distribution function. Thus our model can be thought of as a cumulative link model and can be estimated in a way similar to the estimation of the standard cumulative link model (detailed in Section 3).

However, our model differs from (7) in two ways. First, the cumulative function in our model, $P(Y_1\le F_1^{-1}(t),Y_2\le F_2^{-1}(t)\mid \mathit{x})$, is a bivariate function of (Y₁, Y₂) evaluated on the diagonal at the threshold t. Thus our model is neither a univariate cumulative link model (7) nor a bivariate cumulative link model (Kim, 1995), but a cumulative link model that characterizes the diagonal behavior of the bivariate cumulative distribution function of (Y₁, Y₂). Second, in contrast to (7), where the effect of thresholds, ${\alpha }_m^{\ast }$, is of little interest, our method explicitly models it in the regression Σ_k α_kh_k(t), and uses it as the primary means to describe the reproducibility of the baseline procedure.

3. Estimation

We develop a maximum likelihood approach to estimate the parameters in this model. Similar to the strategy for estimating the standard cumulative link models, our estimation procedure classifies the observations into nonoverlapping ordered categories and fits a multinomial likelihood. Specifically, considering the cutoffs, 0 = t₀ < t₁ < ···< t_M = 1, the candidates from each workflow can be partitioned into M categories by the cutoffs of their scores, such that each category consists of the candidates that are deemed reproducible at t_m but not at t_m−1. That is, for scores ( $Y_{i1}^s,Y_{i2}^s$), i = 1, …, n, from the workflow s, the categories can be defined as ${\mathbb{Y}}_m^s=\{i:{\sum }_{j=1}^2{I}_{ij}^s(t_m)=2\}\backslash \{i:{\sum }_{j=1}^2{I}_{ij}^s(t_{m-1})=2\}$, where $l_{ij}^s(t_m)=I(Y_{ij}^s\le {\mathbb{F}}_j^{s-1}(t_m)\mid {\mathit{x}}^s)$ and ${\mathbb{F}}_j^s$ is the empirical cumulative distribution function of $Y_j^s$. These categories form a multinomial distribution. Let $U_{im}^s=I(i\in {\mathbb{Y}}_m^s\mid {\mathit{x}}^s)$ be the binary indicator for the scores of candidate i assigned by the workflow s to fall in the mth category, then the likelihood function of the multinomial distribution is

$$\begin{gathered} L(\mathit{\theta })=\prod _{s=1}^S\prod _{i=1}^n\prod _{m=1}^M{[P(i\in {\mathbb{Y}}_m^s\mid {\mathit{x}}^s)]}^{U_{im}^s} \\ =\prod _{s=1}^S\prod _{i=1}^n\prod _{m=1}^M{\left[g^{-1}\left(\sum _{k=1}^K{\alpha }_k{h}_k(t_m)+\mathit{W}{(t_m,\beta )}^T{\mathit{x}}^s\right)-g^{-1}\left(\sum _{k=1}^K{\alpha }_k{h}_k(t_{m-1})+\mathit{W}{(t_{m-1},\beta )}^T{\mathit{x}}^s\right)\right]}^{U_{im}^s}, \end{gathered}$$ (8)

where θ = (α^T, β^T)^T.

To fit this model, we first obtain $U_{im}^s$ for each candidate at each cutoff for each workflow, then perform the maximum likelihood estimation. We prove the asymptotic normality of θ̂ by applying the standard theory of maximum likelihood estimation for ordinal regressions (Theorem 1 in Supplementary materials).

4. Simulation studies

We use simulation studies to examine the performance of our method. In particular, we evaluate the accuracy of estimation and type I error under both canonical and misspecified models, as well as the power for detecting differences in reproducibility in the settings resembling high-throughput experiments.

Accuracy of estimation and type I error under canonical models

We first evaluate the performance of our method under canonical models. We generate (Y₁, Y₂) from a Gumbel-Hougaard copula, then estimate the regression coefficient using the corresponding canonical functional choice. Here we choose the association parameter of the copula as θ_G = 1.0, 2.0, and 3.0, corresponding to independence (θ_G = 1.0) and the typical strength of dependence observed in real data (θ_G = 2.0 and 3.0), respectively.

To evaluate the accuracy of our estimation procedure, we consider the baseline model, log(Ψ(t)) = α₁ log(t), and compare α̂₁ with its true value, α₁ = 2^1/θ_G. To evaluate the impact of the spacing of the cutoff points, we perform the estimation with M = 20, 50, 100 equally spaced cutoff points in (0, 1). For each θ_G, we simulate 1000 datasets, each of which consists of the scores of n = 500, 1000, 10000 candidates on a pair of replicates.

As shown in Table 2a, the estimates are reasonably accurate. The spacing of cutoffs with different M’s seems to show little effects on the accuracy and efficiency of estimation in our simulations (Supplementary Table 1). As expected, larger sample sizes improve the accuracy and reduce the variance of estimation (Supplementary Table 1).

Table 2.

Accuracy of estimation and Type I error when the regression model follows the canonical specification or is misspecified. (a) Canonical model specification: data are simulated from a Gumbel-Hougaard copula with θ_G = 1.0, 2.0 and 3.0, and the corresponding canonical regression form is fitted. The regression coefficient α₁ is compared. (b) Misspecified model: data are simulated from a Clayton copula with θ_C = 1.0, 1.2 and 2.0, and the regression model based on the Nelson 4.2.12 copula is fitted. The lower-tail dependence λ_L is compared. The means, the 95% confidence intervals of the estimated parameters and the type I errors are computed based on 1,000 data sets with the sample size of n = 10, 000 and M = 50 equally spaced cutoffs in (0, 1).

(a) Canonical model specification
θG	${\alpha }_1=2^{\frac{1}{{\theta }_G}}$	Estimation		Type I error
		$\widehat{{\alpha }_1}$	95% CI	α = 0.1	α = 0.05	α = 0.01
1.0	2.000	1.996	[1.955, 2.037]	0.095	0.045	0.012
2.0	1.414	1.413	[1.358, 1.468]	0.100	0.049	0.007
3.0	1.260	1.258	[1.344, 1.172]	0.116	0.058	0.009

(b) Misspecified model
θC	${\lambda }_L=2^{-\frac{1}{{\theta }_C}}$	Estimation		Type I error
		λ̂L	95% CI	α = 0.1	α = 0.05	α = 0.01
1.0	0.500	0.503	[0.435, 0.570]	0.097	0.048	0.008
1.2	0.561	0.522	[0.456, 0.587]	0.105	0.055	0.010
2.0	0.707	0.587	[0.528, 0.646]	0.115	0.066	0.015

To assess the type I error for detecting the difference in reproducibility, we simulate the scores of a pair of replicates for two workflows (X = 0, 1) from the Gumbel-Hougaard copula with the same θ for θ = 1.0, 2.0 and 3.0. We then fit the canonical regression model, log(Ψ(t)|X) = α₁ log(t) + βX log(t), and test H₀ : β = 0 using Wald test. For each θ, we simulate 1000 datasets, each of which consists of n = 10, 000 pairs of observations for each workflow. We then fit each model with M = 50 equally spaced cutoffs in (0, 1), and assess type I error rates at the significance levels of 0.01, 0.05 and 0.1. As shown in Table 2a, the empirical type I error is reasonably calibrated at all three significance levels.

Accuracy of estimation and type I error under model misspecfication

We next evaluate the performance of our method when the regression model does not correspond to the distribution that generates the data. In particular, we focus on the situation that the dependence structure of the copula for the regression model is reasonably similar to that of the empirical data, as this is the typical case that misspecification in model selection would occur in practice. To proceed, we generate data from a Clayton copula with an association parameter θ_C, which is not in the homogeneous reproducibility class, and then estimate the regression coefficient using the canonical regression for the Nelsen 4.2.12 copula. These two copulas have similar lower-tail dependence but different upper-tail dependence: Clayton copula has no upper-tail dependence, whereas Nelsen 4.2.12 copula has a positive upper-tail dependence. They are similar to each other when their association parameters are small, but are different in the upper tail when the association parameters are large. Here we simulate data from θ_C =1.0, 1.2 and 2.0 to imitate progressive levels of misspecification. For each θ_C, we simulate 1000 datasets, each of which consists of n = 10, 000 pairs of observations for each workflow, and then fit the regression model using M = 50.

Due to model misspecification, there is no direct correspondence between θ_C and the regression coefficients. However, because the two copulas have the similar lower-tail behavior, one may assess estimation accuracy by comparing the lower-tail dependence of the Nelson 4.2.12 copula computed from the estimated regression coefficients (λ̂_L = 2^{α̂₁/log 2}) with the true value computed from the Clayton copula (λ_L = 2^−1/θ_C) (See Supplementary materials for derivation of lower-tail dependence for these two copulas).

As shown in Table 2b, the 95% confidence interval of λ̂_L covers the true value when the misspecification is moderate (θ_C ≤ 1.2), but it fails to do so when the violation is severe (θ_C = 2.0). Similarly, the type I error for the test of H₀ : β = 0 is reasonably calibrated when the violation is moderate, and it starts to inflate when the violation is severe.

Power for detecting difference in reproducibility in a high-throughput setting

We next evaluate the performance of our method in a simulation resembling high-throughput biological studies. This type of studies typically involves a small subset of candidates that are truly associated with a biological feature and a large subset of irrelevant ones. The significance scores of relevant candidates are generally ranked higher and more consistently across replicates than those of irrelevant ones. The reliability of the findings from these studies largely depends on the agreement of relevant candidates. Therefore, our evaluation focuses on the power for detecting the difference in reproducibility for relevant candidates.

We consider a setting with two workflows, X = 0, 1. Workflow 1 ranks relevant candidates more reproducibly across replicates than workflow 0, and both workflows rank irrelevant candidates with similar level of reproducibility. In an attempt to generate realistic simulations, we follow the simulation in Li et al. (2011) for generating scores of protein-binding sites identified in replicate ChIP-seq experiments. Since the data is not generated from our model, this simulation provides an objective evaluation of the performance and robustness of our method.

For each workflow, we simulate the scores of a pair of replicate samples from a bivariate normal mixture distribution, ${\sum }_{k=0}^1{\pi }_{k}N(\left(\begin{array}{c}{\mu }_k\\ {\mu }_k\end{array}\right),\left(\begin{array}{cc}1& {\rho }_k\\ {\rho }_k& 1\end{array}\right))$, where k = 0, 1 represents irrelevant and relevant candidates, respectively, and π_k represents the proportion of each corresponding category. As in Li et al. (2011), we assume that the scores of irrelevant candidates are independent across replicates, i.e. ρ₀ = 0, and that the scores of relevant candidates are positively associated across replicates, i.e. ρ₁ > 0. To reflect the difference in the reproducibility of relevant candidates, we choose a higher ρ₁ for workflow 1 than for workflow 0, and keep the rest of parameters (μ₁, σ₁, μ₀, σ₀, ρ₀) identical for the two workflows. We select simulation parameters based on the parameters estimated from a ChIP-seq data set in (Li et al., 2011). We set μ₁ = 2.5, σ₁ = 1, μ₀ = 0, σ₀ = 1, ρ₀ = 0 for both workflows, ρ₁ = 0.6 for workflow 0, and ρ₁ = 0.8, 0.9, 0.95 for workflow 1 to simulate different levels of reproducibility for relevant candidates. We further vary π₁ = 0.05, 0.1 and 0.3 to simulate the scenarios with different amounts of real signals. For each set of simulation parameters, we generate 100 datasets, each of which consists of the scores assigned by each of the two workflows on a pair of replicates with n = 10, 000 observations.

As a comparison, we also evaluate reproducibility using the concordance correlation coefficient (CCC) (Lin, 1989), a reproducibility index commonly used for assessing the agreement between readings from two assays. To keep the comparison on the same basis, we compute CCC using the ranks of scores, as our method is essentially based on ranks.

We compare the reproducibility between the two workflows using our method and CCC. As the data (Figure 2a) resembles the shape of the Gumbel-Hougaard copula (Figure 2b), we use the canonical model for the Gumbel-Hougaard copula to fit our data, with M = 50 equally spaced cutoffs in (0, 1), and test the difference in reproducibility using Wald’s test for H₀ : β = 0 at the significance level of α = 0.05. For CCC, we compute its 95% asymptotic confidence interval for the outcome of each workflow and test the difference in reproducibility according to whether the two confidence intervals overlap. CCC and its asymptotic confidence interval are computed using R package EpiR. Power is computed as the percentage of times that a significant difference in reproducibility is detected.

As shown in Table 3, our model consistently shows a higher power than CCC in all the simulations studied here. The gain in power is especially substantial when the proportion of relevant candidates is low. For example, when the proportion of relevant candidates is 10% and ρ₁ for the two workflows are 0.6 and 0.95, respectively, CCC has little power to detect the difference (power=0.02), but our method still maintains a reasonable power (power=0.99).

Table 3.

Power for detecting differences in reproducibility in a simulation resembling a high-throughput setting. For all simulations, μ₁ = 2.5, σ₁ = 1, μ₀ = 0, σ₀ = 1, ρ₀ = 0 for both workflows, and ρ₁ = 0.6 for workflow 0 and ρ₁ = 0.8, 0.9, 0.95 for workflow 1. Three scenarios are considered with the proportion of real signals π = 0.05, 0.1 and 0.3, respectively. For each set of simulation parameters, 100 datasets are generated, each of which consists of 10,000 pairs of observations. The regression model is fitted using M = 50 cutoffs equally spaced in (0, 1). The power is calculated at the significance level of α = 0.1.

ρ1	π = 0.05		π = 0.1		π = 0.3
	regression	CCC	regression	CCC	regression	CCC
0.8	0.01	0.00	0.21	0.01	1.0	0.13
0.9	0.18	0.00	0.88	0.02	1.0	0.32
0.95	0.38	0.04	0.99	0.02	1.0	0.58

5. Application on real data

5.1 Comparing the reproducibility of ChIP-seq peak calling algorithms

We first illustrate our method using a ChIP-seq dataset in Li et al. (2011). In this study, ChIP-seq experiments for the transcription factor CTCF were performed on two biological replicates and CTCF binding sites were identified using multiple algorithms. The goal is to compare the performance of the algorithms and select the best one(s) for building an analysis pipeline for ENCODE production ChIP-seq data (Landt et al., 2012). To compare the reproducibility of identifications across replicates, Li et al. (2011) plotted the correspondence curve for each algorithm and ranked the algorithms according to the curves. Though this ranking is useful, it cannot infer how significant the difference is. The significance, however, is important for algorithm selection, especially when other performance criteria are also considered. For example, if the difference in reproducibility is not significant, then a fast or user-friendly algorithm would be preferred even though it is not the most reproducible one.

Here we use our regression model to compare the reproducibility of six algorithms, MACS, SPP, Peakseq, Cisgenome, Quest and SISSRS. For each algorithm, we compute Ψ(t) from the scores assigned by each algorithm on the two biological replicates using M = 50 equally spaced cutoffs in (0, 1). To select the functional form of the regression model, we examine the rank scatterplots of the scores on the two biological replicates and find that the Gumbel-Hougaard copula is a reasonable fit. This is confirmed by the approximate linear relationship between log(t) and log(Ψ(t)) shown in most peak callers (Supplementary Figure 1). Therefore, we fit the regression model

$$log(\mathrm{\Psi }(t))={\alpha }_{1}log(t)+{\beta }_{M}log(t)X_M+{\beta }_{P}log(t)X_P+{\beta }_{C}log(t)X_C+{\beta }_{Q}log(t)X_Q+{\beta }_{S}log(t)X_S,$$

where SPP is used as the baseline and X_M,X_P,X_C,X_Q and X_S are the dummy variables for MACS, Peakseq, Cisgenome, Quest and SISSRS, respectively.

Following Li et al. (2011), we perform our analysis on the binding regions that are commonly identified on both replicates. To ensure the comparison is on the same basis across algorithms, we use the most significant n = 6, 000 common regions identified by each algorithm, ranked based on the significance score on replicate 1, in our analysis.

Table 4 summarizes the results from our analysis. According to the 95% confidence intervals of β’s, we classify the algorithms into three tiers that are significantly different in reproducibility. The most reproducible tier consists of Peakseq, SPP, Quest and MACS. Peakseq is slightly more reproducible and Quest and MACS are slightly less reproducible than SPP, but the difference is not significant. At a given threshold, for example, t = 0.05, the estimated probabilities of being reproducibly reported in the top 100t% are t^−0.030 = 1.094 (95% CI: [0.959, 1.244]), t^0.019 = 0.945 (95% CI: [0.804, 1.244]), t^0.048 = 0.866 (95% CI: [0.737, 1.018]) times as high for Peakseq, Quest and MACS as for SPP, respectively. The next tier consists of Cisgenome. Its estimated probability of being reproducibly reported in the top 5% as t^0.094 = 0.755 (95% CI: [0.640, 0.890]) times as high as for SPP. SISSRS is the least reproducible algorithm in the comparison. The estimated probability of being reproducibly reported in the top 5% is only t^0.452 = 0.258 (95% CI: [0.214, 0.311]) times as high as for SPP. The quantitative summary and statistical inference obtained above are more informative than a ranking for selecting algorithms, especially when multiple selection criteria are considered.

Table 4.

Estimated regression coefficients for evaluating the reproducibility of peak calling algorithms. SPP is used as the baseline.

		Estimate	95% Confidence Interval
Baseline	α1	1.483	[1.446, 1.521]
MACS	βM	0.048	[−0.006, 0.102]
Peakseq	βP	−0.030	[−0.083, 0.022]
Cisgenome	βC	0.094	[0.039, 0.149]
Quest	βQ	0.019	[−0.034, 0.073]
SISSRS	βS	0.452	[0.390, 0.514]

5.2 Application on a multiple-laboratory multiple-platform microarray dataset

We now apply our method to the multiple-laboratory microarray study in the introduction (Irizarry et al., 2005). This study was conducted by a consortium of ten labs to assess the intra- and inter-platform agreement of the gene expression levels measured on three microarray platforms. A major goal of this study was to assess how differences in platforms and labs contribute to the variation in gene expression measurements. In particular, it aimed to investigate if failing to control for lab effects is the major cause of the lack of reproducibility reported in previous studies. To standardize the comparison, all labs were provided identical RNA samples, which consist of two technical replicates. For each replicate, each lab measured the gene expression levels on at least one of the three microarray platforms. The detailed study design can be found in Irizarry et al. (2005).

To compare the reproducibility of the platforms, Irizarry et al. (2005) assessed the concordance of differential expression levels between the two replicates for each platform-lab combination, using a comprehensive set of descriptive and graphical statistics, including correlation coefficients between gene expression levels across replicates, the proportion of common identifications among a series of top-n ranked genes, and the CAT plot. Though these statistics are informative, none of them succinctly summarizes platform effects and lab effects on reproducibility, provides any statistical inference, or evaluates platform effects while controlling for the lab effects.

Here we use our regression framework to characterize lab effects and platform effects. Because we were only able to obtain the data from Affymetrix and 2-Color-oligo platforms for Lab 1 and Lab 2 using the online scripts in Irizarry et al. (2005), we only include these two platforms and two labs in our analysis. As the number of differentially expressed genes in this sample is small comparing to the total number of genes, we perform our analysis for the n = 200 most differentially expressed genes. A subset of data is shown in Table 5. For each platform-lab combination, we compute Ψ(t) using the absolute log2 fold change of gene expression levels on the two replicate samples.

The rank scatterplot of the empirical data shows a dependence structure similar to that of the Nelsen (4.2.12) copula (Figure 3a–b). Therefore, the canonical regression form of this copula (Table 1) is a reasonable choice. One appeal of this model is that the strength of association between (Y₁, Y₂) is involved only through the intercept term in the regression model, without involving t, thus there is no need to include the interaction between covariates and t. Figure 3c confirms that there is an approximately linear relationship between logit(Ψ(t)) and logit(t) in all the four platform-lab combinations. Therefore, we fit the model

$$\text{logit}(\mathrm{\Psi }(t))={\alpha }_1+{\alpha }_2\text{logit}(t)+{\beta }_L{X}_L+{\beta }_P{X}_P$$ (9)

where Lab 1 and Affymetrix arrays are used as baseline, and X_L and X_P are binary indicator variables for Lab 2 and 2-color Oligo array, respectively, with M = 50 equally spaced cutoffs in (0, 1). Here we choose to estimate α₂, instead of using the canonical value α₂ = 1, to allow additional flexibility in model fitting. Furthermore, in light of the possible interactions between lab, platform and logit(t), we also fit a model with interaction terms: logit(Ψ(t)) = α₁+α₂logit(t)+β_LX_L+β_PX_P+β_LtX_Llogit(t)+β_PtX_P logit(t)+β_LPX_LX_P+β_LPtX_LX_P logit(t). However, none of the interaction terms are significant (95% CIs: (−0.148, 0.159) for β_Lt, (−0.024, 0.309) for β_Pt, (−0.458, 0.558) for β_LP and (−0.299, 0.165) for β_LPt) (Supplementary Table 2). Therefore, we choose (9) as our final model.

As shown in Table 5, our model indicates that two-color Oligo arrays are significantly less reproducible than Affymetrix arrays in ranking differentially expressed genes. Given a thresh-old t, the estimated odds of being reproducibly reported in the top 100t% is exp(−0.274) = 0.760 (95% CI=(0.598, 0.967)) times as high for two-color Oligo arrays as for Affymetrix arrays, when controlling the lab effects. When controlling the platform effects, Lab 2 is slightly more reproducible than Lab 1 (estimated odds ratio exp(0.034) = 1.035), but the difference is not significant (95% CI=(0.814, 1.314)). These results confirm the trend illustrated in the CAT plot and the correspondence curve (Figure 1). More importantly, the coefficients from our regression model provide a succinct summary to quantify the significance of each covariate, while adjusting for the other variable.

6. Discussion

In this work, we present a novel regression modeling framework for assessing the influence of operational factors on the reproducibility of high-throughput ranking systems. This framework succinctly quantifies the simultaneous and independent effects of multiple covariates. It thus provides a parametric alternative to existing graphical tools for comparing and benchmarking the reproducibility of different workflows in high-throughput experiments. It is also applicable to other settings that involve screening top-ranked entries, for example, selecting signals indicating brain activities from fMRI images (Benjamini and Heller, 2008).

This work also leads to the discovery of a class of Archimedean copulas that have the property of homogeneous reproducibility. To the best of our knowledge, this property and this class have not been reported in literature. Our work reveals a new way to interpret and utilize these copulas. Further utilities of these copulas as modeling tools will be explored.

Our method can be extended in several ways. First, the assumption of homogeneous reproducibility in the current model may be violated in real applications, for instance, reproducibility may be different between top-ranked and bottom-ranked candidates. Though our simulations shows that this method still maintains a high power in this case, it can be improved by using a segmented regression model. Another extension is to handle missing data, which is a common concern in real applications. As missing values in high-throughput experiments are often generated when measurements or significance are below threshold, one possibility is to extend our likelihood function to incorporate left truncation.