Abstract
Inter-pixel communication and anti-charge sharing (ACS) technologies have been introduced to photon counting detector (PCD) systems to address the undesirable charge sharing problem. In addition to improving the energy resolution of PCD, ACS may also influence other aspects of PCD performance such as detector multiplicity (i.e., the number of pixels triggered by each interacted photon) and detective quantum efficiency (DQE). In this work, a theoretical model was developed to address how ACS impacts the multiplicity and zero-frequency DQE [DQE(0)] of PCD systems. The work focused on cadmium telluride (CdTe)-based PCD that often involves the generation and transport of K-fluorescence photons. Under the parallel cascaded systems analysis framework, the theory takes both photoelectric and scattering effects into account, and it also considers both the reabsorption and escape of photons. In a new theoretical treatment of ACS, it was considered as a modified version of the conventional single pixel (i.e., non-ACS) mode, but with reduced charge spreading distance and K-fluorescence travel distance. The proposed theoretical model does not require prior knowledge of the detailed ACS implementation method for each specific PCD, and its parameters can be experimentally determined using a radioisotope without invoking any Monte-Carlo simulation. After determining the model parameters, independent validation experiments were performed using a diagnostic x-ray tube and four different polychromatic beams (from 50 to 120 kVp). Both the theoretical and experimental results demonstrate that ACS increased the first and second moments of multiplicity for a majority of the x-ray energy and threshold levels tested, except when the threshold level was much lower than the x-ray energy level. However, ACS always improved DQE(0) at all energy and threshold levels tested.
Keywords: Photon counting detector, zero-frequency DQE, cascaded systems analysis, anti-charge sharing, CdTe, x-ray imaging
1. Introduction
Advances in single photon counting detector (PCD) technology are opening up opportunities to improve the performance of existing x-ray imaging methods (Shikhaliev 2008, Schmidt 2009, Yu, Leng, Jorgensen, Li, Gutjahr, Chen, Halaweish, Kappler, Yu, Ritman & McCollough 2016, Lee et al. 2016, Leng et al. 2016), and enabling new imaging technologies and applications, including spectral CT imaging with multiple material bases (Shikhaliev & Fritz 2011, Wang et al. 2011, Symons et al. 2017, Yu, Li, Leng & McCollough 2016), K-edge imaging (Schlomka et al. 2008, Feuerlein et al. 2008, Roessl et al. 2011, Sato et al. 2012, Rink et al. 2013), simultaneous multi-agent imaging (Schlomka et al. 2008, Symons et al. 2017), molecular CT with nanoparticle contrast agents and personalized medicine (Taguchi & Iwanczyk 2013), energy resolving x-ray phase contrast imaging (Pelzer et al. 2013, Thuering et al. 2013, Ge et al. 2016), etc.
However, it is fair to say that the current PCD technology is not flawless and is faced with several challenges. For example, charge sharing and pulse pileup may cause false counts and distort the energy response of PCD (Wielopolski & Gardner 1976, Johns & Yaffe 1987, Barradas & Reis 2006, Chmeissani & Mikulec 2001, Pennicard et al. 2010, Gimenez et al. 2011a, Taguchi et al. 2010, Taguchi et al. 2011, Taguchi & Iwanczyk 2013, Ballabriga et al. 2016). The charge sharing effect is usually induced by the lateral spreading of primary and secondary quanta in the photoconductor, and can result in two or more neighboring pixels being triggered by a single input x-ray photon (Chmeissani & Mikulec 2001, Pennicard et al. 2010, Gimenez et al. 2011a, Gimenez et al. 2011b, Ballabriga et al. 2016). Charge sharing not only distorts the fidelity of the detector’s energy response, but may also introduce undesirable spatial and energy correlations in the measured image. In order to mitigate charge sharing, the so-called anti-charge sharing (ACS) or anti-coincidence technologies have been developed and applied to many state-of-the-art PCD systems (Ballabriga et al. 2007, Gimenez et al. 2011b, Ballabriga et al. 2013, Koenig et al. 2013, Koenig et al. 2014, Hamann et al. 2015, Ballabriga et al. 2016).
The basic idea of ACS is to determine whether there are coincident secondary quanta collected in more than one pixel within a local area and assign a count to only the pixel most likely struck by an x-ray photon. For example, in the initial version of the Medipix3 PCD, ACS was implemented using a readout chip architecture that places a summing node at the corner of each pixel (Ballabriga et al. 2007). After the charge summation process, the summed charge of this node is then compared with both a predefined charge threshold (in a discriminator) and the charges of its neighboring summing nodes (in an arbitration circuit); an x-ray photon count can be assigned to the current node only if its summed charge (1) exceeds the threshold and (2) wins the arbitration process. Although this ACS architecture effectively improves the energy resolution of the PCD (Ballabriga et al. 2007), its performance is particularly sensitive to the charge threshold dispersion, as counts could be preferentially assigned to nodes with lower threshold values (Gimenez et al. 2011b, Pennicard et al. 2011). In a newer version of Medipix3, namely Medipix3RX, the ACS architecture was modified to reduce the impact of threshold dispersion to ACS (Ballabriga et al. 2013, Koenig et al. 2013, Koenig et al. 2014, Hamann et al. 2015, Ballabriga et al. 2016). Description of the Medipix3RX ACS architecture is reviewed later in section 2.7.2. Experimental studies have demonstrated that this newer architecture improves image uniformity, since it is more robust against inter-pixel threshold dispersion (Ballabriga et al. 2013).
Besides the impact to image uniformity and detector energy resolution, ACS could also influence other aspects of the PCD performance such as noise power spectrum (NPS), modulation transfer function (MTF), and detective quantum efficiency (DQE). (Pennicard et al. 2011, Ballabriga et al. 2013, Ullberg et al. 2013, Koenig et al. 2014, Xu et al. 2014, Ji et al. 2017). For example, Ballabriga et al. experimentally demonstrated that the mean multiplicity (i.e. number of pixels triggered by each interacted photon) of Medipix3RX was reduced by ACS at relatively low threshold levels. However, at higher threshold levels, ACS led to an opposite effect: the mean multiplicity was actually increased (Ballabriga et al. 2013). Despite the possible reduction in mean multiplicity, another experimental study found that ACS always improves zero-frequency detective quantum efficiency [DQE(0)], and the relative improvement factor strongly depends on the x-ray energy and threshold level (Koenig et al. 2014).
Given the close relationship between the DQE(0) and radiation dose efficiency of an x-ray imaging system, detailed knowledge of how ACS impacts the DQE(0) of a PCD is crucial for employing ACS in medical imaging. In addition to extensive experimental characterizations, theoretical modeling is another important approach to offering insight into this topic. For conventional energy integrating detectors (EIDs), theoretical modeling of DQE(0) was performed using cascaded linear system theory. For a PCD, an additional model needs to be developed to accommodate nonlinear processes such as energy thresholding. Tanguay et al. proposed a DQE model for a PCD using the transfer of probability density distribution from one sub-detector stage to another (Tanguay et al. 2013). The model was extended to parallel cascaded systems in a later publication (Tanguay et al. 2015). Both works assumed the absence of the charge diffusion. In another theoretical model developed by Xu et al. (Xu et al. 2014), charge sharing was assumed to be solely induced by charge diffusion; no K-fluorescence effect was considered as the authors focused on a silicon (Si)-based PCD. In that work, the contribution of ACS to detector output was incorporated via a relative reduction factor for the likelihood of false counts. Although this reduction factor should depend on the number of false counts triggered by each photon, a practical approach to determining the corresponding dependence is still lacking, so the authors had to empirically choose a constant value for this factor.
The work presented in this paper was driven by the following central question: how to incorporate both K-fluorescence and ACS into a theoretical model of a PCD system, so that one can gain more insight into the dependence of the PCD DQE(0) on the ACS technology? This work focuses on a cadmium telluride (CdTe)-based PCD system due to the prevalence of charge sharing and K-fluorescence in this type of detector: both Cd and Te can generate a significant amount of K-fluorescence photons with energies high enough to travel out of a single detector pixel (Shikhaliev et al. 2009). Different from previous models, this work did not introduce any additional signal and noise transfer stage for the ACS process; instead, ACS was modeled together with the energy thresholding process as a single stage, and the impact of charge summation and reassignment during ACS was quantified by a reduction factor for the K-fluorescence travel distance and charge cloud radius in CdTe. With this new treatment of the ACS process, the impact of ACS to an arbitrary level of multiplicity was modeled as a function of x-ray energy and threshold level, and the DQE(0) of a PCD under either monoenergetic or polychromatic radiation was also theoretically derived. Another contribution of this work was the development of an experimental methodology to determine the ACS-related reduction factor for a given PCD system. Once the parameter was determined using a quasi-monoenergetic γ-ray source (Am-241, 59.5 keV), independent experimental validation of the theoretical model was performed using polychromatic x-rays (rotating-anode diagnostic x-ray tube, potentials ranging from 50 to 120 kVp).
2. Theoretical model
For a given x-ray detector system, its zero-frequency DQE characterizes how much the average detector output fluctuates compared with the input Poisson process. Its general formula is given by
| (1) |
For the particular case of a pixelated photon counting detector, equation (1) is reduced to the following form (Michel et al. 2006):
| (2) |
where ε denotes the x-ray absorption efficiency of the photoconductive layer of the PCD, and m denotes the so-called multiplicity of the PCD (Michel et al. 2006, Koenig et al. 2014), which quantifies the number of PCD pixels triggered a single interacted photon.
The modeling of ε is relatively straightforward as shown later in section 2.1. In order to pinpoint the impact of ACS on DQE in Eq. (2), the theoretical modeling in this paper focuses on connecting multiplicity m with ACS and other PCD system parameters. Towards this goal, cascaded systems analysis of CdTe-based PCD was performed.
In a typical cascaded systems analysis, an imaging system is decomposed into different sub-imaging stages; the transfer of signal or noise is traced through these sub-stages, so that the signal or noise properties of the final image can be quantitatively (or qualitatively) related to the input and parameters of the imaging system (Rabbani et al. 1987, Cunningham et al. 1994, Yao & Cunningham 2001, Siewerdsen et al. 1997, Bissonnette et al. 1997, Siewerdsen et al. 1998, Drake et al. 2000, Zhao et al. 2001, Ganguly et al. 2003, Vedantham et al. 2004, Richard & Siewerdsen 2008, Marchal 2010, Tward & Siewerdsen 2008, Tward & Siewerdsen 2009, Gang et al. 2011, Prakash et al. 2011, Li et al. 2013, Gang et al. 2014, Tanguay et al. 2013, Xu et al. 2014, Tanguay et al. 2015, Li & Chen 2016). In this work, cascaded systems analysis was used to establish the needed quantitative relationship between the DQE(0) of a CdTe-based PCD system and parameters such as energy threshold, ACS, and material properties of CdTe. Based on the physical properties of the CdTe material (Iwanczyk et al. 1979, Owens & Peacock 2004, Thompson et al. 2001, Knoll 2010, Russo & Del Guerra 2014) summarized in table 1, x-ray-CdTe interactions often result in K-fluorescence emissions with considerable energies (> 25 keV), which naturally calls for the use of parallel cascades (Cunningham 1998, Zhao et al. 2001, Yao & Cunningham 2001, Ganguly et al. 2003, Vedantham et al. 2004, Tanguay et al. 2013, Tanguay et al. 2015), in addition to serial cascades (Cunningham et al. 1994).
Table 1.
Physical properties of CdTe. For comparison, properties of silicon (Si) are also listed. (PE: photoelectric effect)
| Photoconductor | Si | CdTe |
|---|---|---|
| Effective atomic number (Z) | 14 | 50 |
| Mass density [g/cm3] | 2.33 | 5.85 |
| Bandgap (eV) | 1.12 | 1.44 |
| Electron-hole pair creation energy [eV] | 3.62 | 4.43 |
| Electron mobility [cm2/(V·s)] | 1400 | 1100 |
| Hole mobility [cm2/(V·s)] | 480 | 100 |
| Electron life time [s] | >10−3 | 3 × 10−6 |
| Hole life time [s] | 2 × 10−3 | 2 × 10−6 |
| K-edge energy [keV] | 1.84 | 26.7 (Cd); 31.8 (Te) |
| K-shell contribution to PE (ξ) | 0.90 | 0.85 |
| K-fluorescence yield (ω) | 0.04 | 0.84 (Cd); 0.88 (Te) |
| Kα fluorescence energy [keV] | 1.7 | 23.2 (Cd); 27.2 (Te) |
| Kβ fluorescence energy [keV] | 1.8 | 26.1 (Cd); 31.0 (Te) |
| Probability of Kα production | 0.99 | 0.84 (Cd); 0.83 (Te) |
| Probability of Kβ production | 0.01 | 0.16 (Cd); 0.17 (Te) |
| Fano factor (F) | 0.1 | 0.1 |
2.1. Stage 1: Interaction of individual x-ray photon with CdTe
When an x-ray photon strikes the detector, it may either interact with the CdTe layer, or pass through the layer without interaction. The probability of interaction is essentially the x-ray absorption efficiency ε in equation (2). For a given x-ray energy E, ε is related to the x-ray attenuation coefficient (μ) and thickness (D) of CdTe by
| (3) |
where E denotes x-ray energy.
2.2. Stage 2: Generation of secondary quanta
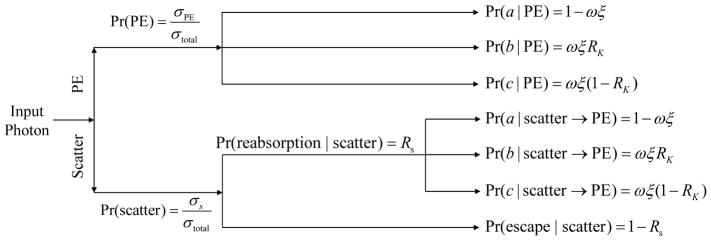
For an x-ray photon hitting the detector at location (xi, yi), it can deposit energy via two major gateways, one starts with photoelectric effect (PE), while the other one starts with x-ray scattering and eventually involves PE, as shown in figure 1.
Figure 1.
Summary of parallel cascades that lead to electron-hole pairs after x ray- CdTe interaction.
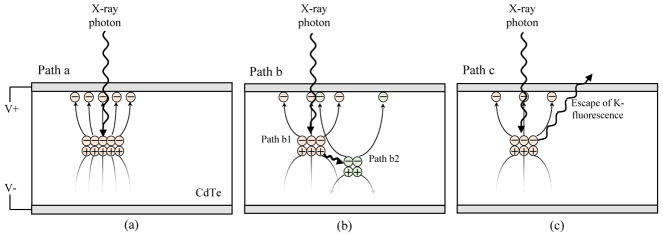
For photons interacting with CdTe through the PE without scattering, the transfer of photon energy can be divided into three parallel paths a, b, and c (figure 2). Detailed description of the parallel cascade can be found in (Zhao et al. 2001), therefore only a brief summary is provided here. For path a, no K-fluorescence is generated, and the energy (denoted as E) of the x-ray photon is locally deposited and converted into electron-hole pairs. For path b, a K-fluorescence photon is generated by the x-ray-CdTe interaction, and the K-fluorescence photon could travel a certain distance to another location [denoted as (xi + ΔxK, yi + ΔyK)] before being reabsorbed by the CdTe layer. The initial interaction is denoted as path b1 while the K-fluorescence reabsorption is denoted as path b2. For path c, a K-fluorescence photon is generated, but ultimately escapes from the CdTe layer, carrying away a fraction of the input photon energy.
Figure 2.
The three paths to generate electron-hole pairs after photoelectric effect.
Given the condition that the x-ray photon is absorbed through the PE, the probability for each of the first three paths (a, b, c) is:
| (4) |
| (5) |
| (6) |
where ξ denotes the fraction of K-shell interaction in each photoelectric event, ω denotes the K-fluorescence yield, and RK is the probability of the K-fluorescence reabsorption, which is related to the incident photon energy and the materiel thickness (Zhao et al. 2001, Sultana et al. 2009). The mean number of electron-hole pairs generated through each path is given by
| (7) |
| (8) |
| (9) |
Here W is the mean energy needed to generate an electron-hole pair. For other processes that start with x-ray scattering, either coherently (Rayleigh) or incoherently (Compton), the scattered photon may eventually be reabsorbed by CdTe and deposit energy. With the energy range of diagnostic x-rays, the scattering cross-section for x-ray scattering contributes less than 10% of the total cross-section; the likelihood for cascaded multi-scattering is even smaller (<1%). Therefore, this work only considered single scattering, followed by either an escape or a photoelectric absorption of the scattered photon.
Unlike Rayleigh scattering that does not deposit energy at the scattering site, Compton scattering could deposit a small fraction of energy, denoted as Erecoil, locally to a charged particle. However, even for a 100 keV x-ray photon, the average value of Erecoil is only 14 keV, which is often below the lowest energy threshold level of the PCD. Therefore, even for Compton scattering, locally deposited energy is ignored, and this work only considered energy deposited remotely via reabsorption of the scattered x-ray photon. On average, the energy of the scattered photon is:
| (10) |
where σR and σC are the cross-sections of Rayleigh and Compton scattering respectively, and σs is the total cross-section for x-ray scattering. After scattering, the scattered photon could follow any of the three paths (a, b, c), or it could escape from the CdTe layer. A term Rs is used to denote the mean likelihood for the scattered photon to be reabsorbed.
For a given path, the variance of q2 is related to q̄2 and the Fano factor (Fano 1947) of CdTe by
| (11) |
Although a single interacted photon follows only one path, the final model of the DQE(0) needs to take all possible paths in figure 1 into account. From Stage 3 to Stage 8, each path is discussed separately, and later in section 2.8, the joint contribution of all parallel paths to the DQE(0) is presented.
2.3. Stage 3: Spatial spreading of secondary quanta
After being generated at a location of (x0, y0) in the 2D detector plane, the secondary quanta (electrons and holes) will be driven toward the electrode by an applied external electric field. Based on the mobility and life time of electrons and holes in CdTe (table 1), hole transport contributes little to the measured detector signal if the pitch of the positive electrode array is much smaller than the thickness of photoconductive layer (Barrett et al. 1995). For the PCD used in this work, the electrode pitch (0.1 mm) is only 5% of the CdTe thickness (2 mm). Therefore, the following analysis focuses only on the transport and collection of electrons.
Due to the Coulomb force and other physical mechanisms, electrons may also diffuse laterally while drifting towards the electrode. In literature, the lateral spreading of electrons was empirically modeled as a normal distribution function (Xu et al. 2014), which provides the probability for an electron to travel from (x0, y0) to (x, y) as
| (12) |
Here re characterizes the mean radius of the charge cloud.
For path a and c, (x0, y0) is the same as the initial x-ray-CdTe interaction location (xi, yi). Taking path a as an example, the expected number of quanta in a small area of (Δa) centred at (x, y) is given by
| (13) |
The variance of is related to the variance of by
| (14) |
For path b, q̄3(x, y|xi, yi) is jointly determined by the two sub-paths (b1 and b2) by
| (15) |
The variance of is given by
| (16) |
Section 2.8 will present how to incorporate the stochastic nature of (ΔxK, ΔyK) into the theoretical model.
For paths starting with an x-ray scattering, the corresponding formulas for q̄3 and are similar to those of the PE-only processes, except that one should use scattered photon energy Es instead of E. As shown in Appendix C, for the specific purpose of DQE modeling, it is unnecessary to replace (xi, yi) by the actual reabsorption position of the scattered photon when implementing equation (12).
2.4. Stage 4: Collection of secondary quanta
Among all secondary quanta generated in Stage 2, only a fraction will eventually be collected by the electrodes, while the remaining will be lost due to mechanisms such as space charge buildup and acceptor capturing. The loss of secondary quanta during the collection process can be considered as a binomial selection process, which has a expected gain value of ḡ4 and variance of . Within an area of Δa centred at (x, y), the expected number of collected secondary quanta is given by
| (17) |
Based on the noise transfer properties of stochastic gain process (Shockley & Pierce 1938, Mandel 1959, Zweig 1965, Jone 1959), the variance of q4 is given by
| (18) |
Equations (17) and (18) are applicable to all parallel paths.
2.5. Stage 5: Integration of secondary quanta by pixel electrode
For a detector pixel centred at (x, y) in the electrode plane, it would integrate those electrons collected within its l × l pixel electrode, namely:
| (19) |
For a given photon interaction, q4 collected at different (x, y) location are fully correlated. As a result, the noise standard deviation (note: not noise variance) of q5 and q4 are related by
| (20) |
2.6. Stage 6: Additive noise from readout electronics
This stage models the additive noise from charge sensitive amplifiers, pulse shaper, and other components in the charge readout circuit. For a given pixel, the total (expected) number of electrons after this stage is
| (21) |
and the total noise variance after this stage is
| (22) |
where ē in eq. (21) and in eq. (22) denote, respectively, the mean and variance of the number of electrons introduced by the readout electronics.
2.7. Stage 7: Anti-charge sharing and energy thresholding
2.7.1. Single pixel mode
For a photon counting pixel detector without ACS (or with ACS disabled), the detection mode is often referred to as single pixel mode, and the following operations are performed independently for different detector pixels: First, the output signal of Stage 6 is fed to a discriminator and compared with a voltage offset, whose value is usually determined to a global threshold level specified by the user. With proper energy calibration, this global threshold may appear as an energy threshold to the user. In passing this global threshold to individual pixels, the voltage offset received by each discriminator often experiences certain inter-pixel random variations due to mismatch in the transistors of different pixels, leading to the so-called threshold dispersion effect (Ballabriga et al. 2007, Gimenez et al. 2011b, Pennicard et al. 2011). A proper threshold equalization process can be used to mitigate threshold dispersion, and improved designs of PCD readout chips have also reduced the influence of threshold dispersion, particularly for the ACS mode (Pennicard et al. 2011, Ballabriga et al. 2013). In this work, threshold dispersion is not included in the theoretical model, but it could be an additional factor that may impact DQE.
Mathematically, the output of Stage 7 for the single pixel mode is given by
| (23) (24) |
where qt is the amount of charge that corresponds to the voltage threshold applied to the discriminator. Thresholding is essentially a binomial selection process with the following expected outcome
| (25) |
Pr(q6 = q′; x, y|xi, yi) is the probability of collecting q′ electrons at (x, y) from an x-ray photon hitting the detector surface at (xi, yi). When q̄6 is large enough, Pr(q6 = q′; x, y|xi, yi) can be approximated by the following normal distribution function
| (26) |
By combining equation (26) and (25), q̄7(qt, x, y|xi, yi) is given as
| (27) |
where erf(·) denotes the error function. For each of the parallel paths, Appendix A provides additional derivations that quantitatively relate q̄7 with detector parameters such as the charge cloud radius (re) and the mean K-fluorescence path length (Δ̄xK, Δ̄yK).
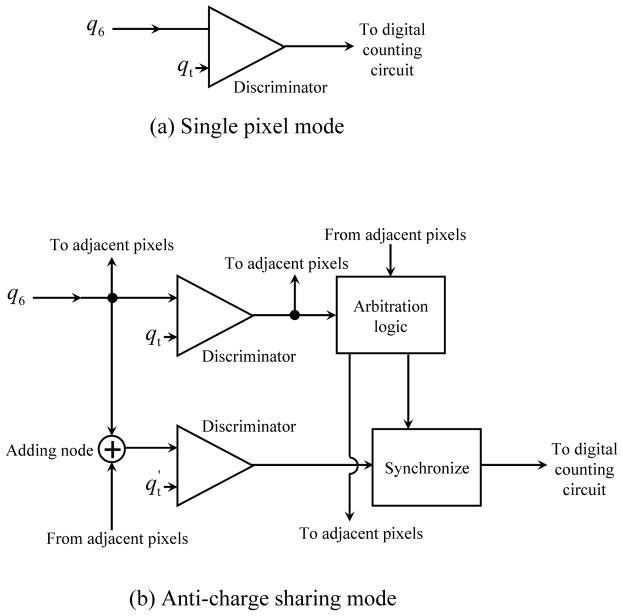
2.7.2. Anti-charge sharing mode
Unlike the single pixel mode, the ACS mode involves inter-pixel communication. Taking the architecture of Medipix3RX as an example (figure 3): The charge deposited in a pixel is first compared with a pixel-level threshold qt in a discriminator. The output of this discriminator feeds to a network of arbitration circuits that determine whether the current pixel has the largest charge deposition compared to its neighbors (Ballabriga et al. 2013). In parallel to the process, the summing nodes located at the corners between pixels integrate the charge in clusters of 2 × 2 pixels. The summed charge of each node is then compared to a node-level threshold in another discriminator. If (1) charge deposited in a pixel exceeds qt, and (2) is the highest with respect to its neighbors, and (3) at least one adjacent adding node exceeds , a count is assigned to this pixel. qt is usually set to be small enough (e.g., 1/4 of the minimal x-ray energy), so that even with charge sharing, charge deposited in individual pixels could exceed this threshold (Pennicard et al. 2011). In this architecture, the pixel charge governs the “arbitration” process, while the summing node dominates the energy thresholding process.
Figure 3.
Comparison of the single pixel mode and anti-charge sharing mode.
To model the impact of ACS to DQE, in principle one needs to know not only the probability density function (PDF) of q6 ≥ qt, but also other information: the output (voltage and duration) of each discriminator; the PDF of winning the arbitration process; the PDF for the shared charge being collected in the neighboring 2×2 pixels; the PDF for the summed charge to exceed . Additionally, one needs to know the implementation method of ACS, which may vary across PCD models and manufacturers.
This work took a different approach: Rather than modeling each of these PDFs based on a priori knowledge of the ACS architecture, the ACS mode was treated as a modified single pixel mode. No matter what intermediate operations are performed during ACS, its outcome is either one or zero count for a given pixel. The major difference between ACS and single pixel mode is that the charge sharing effect is less pronounced. For single pixel mode, the severity of charge sharing is primarily determined by two parameters: effective charge spreading radius (denoted as re), and mean K-fluorescence path length (denoted as Δ̄K). In ACS, reallocating shared charge back to a single pixel has similar effect as reducing re and Δ̄K as follows
| (28) |
| (29) |
where κ denotes the percent distance reduction factor induced by ACS. The use of κ enables the ACS mode to be approximated by the single pixel mode: derivation of q̄7 for the ACS mode is the same as that of the single pixel mode, except that and replace Δ̄K and re (as detailed in Appendix A). Section 3.2 describes how to determine κ for a given PCD system without prior knowledge of the detailed ACS implementation method.
2.8. Summary: multiplicity and DQE(0) of PCD
According to equation (2), the DQE(0) of a PCD system is directly related to m̄ and . Based on the model of q̄7 presented in the previous sections, both m̄ and can be analytically derived (Appendix B). For the first three paths (a, b, c), the first moment of multiplicity is related to q̄7 by
| (30) |
The second moment of multiplicity is given by
| (31) |
In equations (30)–(31), superscript j denotes one of the three paths (a, b, c), and the dependence of q̄7 on x-ray energy E is explicitly indicated.
If we exclude scattering and only consider the photoelectric effect (PE), m̄ and need to take all three paths (a, b, c) into account:
| (32) |
| (33) |
For processes that start with x-ray scattering but eventually end with photoelectric absorption of the scattered photon, Appendix C shows that the corresponding m̄ and is given by
| (34) |
| (35) |
where Es denotes the mean energy of the scattered photon [equation (10)].
When all photoelectric and scattering process are combined,
| (36) |
| (37) |
where σPE and σtotal denote the photoelectric and total x-ray interaction cross-section of CdTe, respectively. In equation (37), the reasorption fraction of the scattered photon Rs is used here to exclude scattered photons that escape from CdTe.
In the case of polychromatic radiation, the DQE of a PCD is related to m̄(qt, E) and by (Appendix D)
| (38) |
where Ω(E) denotes normalized x-ray spectrum.
3. Experimental material and methods
3.1. Experimental PCD system
An experimental CdTe-based PCD system (Model XC-FLITE X1, Xcounter AB, Sweden) was used in this work. Major parameters of this experimental PCD system are listed in table 2. Calibration of the energy threshold of this PCD system was performed within the range of [17, 80] keV using the method reported in (Ge et al. 2018). Beyond 80 keV, the correspondence between the actual x-ray energy and the detector threshold significantly deviates from that of the calibrated range and became increasingly nonlinear. Therefore, no experiment was performed with energy threshold above 80 keV.
Table 2.
Parameters of the experimental PCD system
| Conversion type | Direct |
| Conversion material | CdTe |
| Dead time, single pixel mode (ns) | 140 |
| Dead time, ACS mode, (ns) | 550 |
| CdTe thickness D (mm) | 2 |
| CdTe area (cm×cm) | 15.5 × 1.3 |
| Max. coverage (cm×cm) | 15.5 × 13.5 |
| Pixel size l (μm) | 100 |
| Max. frame rate (fps) | 1000 |
| Readout chip | CMOS |
| Bit depth | 12 |
| Fill factor | 100% |
| Charge collection efficiency ḡ4 | 0.95 |
| Electronic noise σe (electrons) | 1080 |
| Δ̄K (Kα of Cd, in μm) | 88 |
| Δ̄K (Kβ of Cd, in μm) | 122 |
| Δ̄K (Kα of Te, in μm) | 45 |
| Δ̄K (Kβ of Te, in μm) | 64 |
3.2. Determination of model parameters
Among all parameters involved in the theoretical model, most of their values can be found in published literature (Redus et al. 2009, Sultana et al. 2009, Knoll 2010, Matz & Weidner 1998, Veale et al. 2014, Iwanczyk et al. 2009, Xu et al. 2014). For parameters that are directly related to the material properties of CdTe (e.g., ω and ξ), their values can be found in table 1. With regard to the average number of electrons added by readout electronics (ē), its impact to q̄6 has been compensated through the threshold calibration process. Therefore, its value was set to zero. The electronic noise σe was determined based on a published reference (Iwanczyk et al. 2009). The effective path length of K-fluorescence photon (Δ̄K) was calculated analytically using the method described in Appendix A. The value of parameter RK (likelihood of K-fluorescence reabsorption) was numerically calculated based on the method described in (Sultana et al. 2009). The value of parameter Rs (likelihood to reabsorb scattered photon) was numerically calculated based on the method described in (Xu et al. 2014). Table 2 lists the estimated values of several other parameters. Figure 4 plots RK and Rs versus x-ray energy E.
Figure 4.
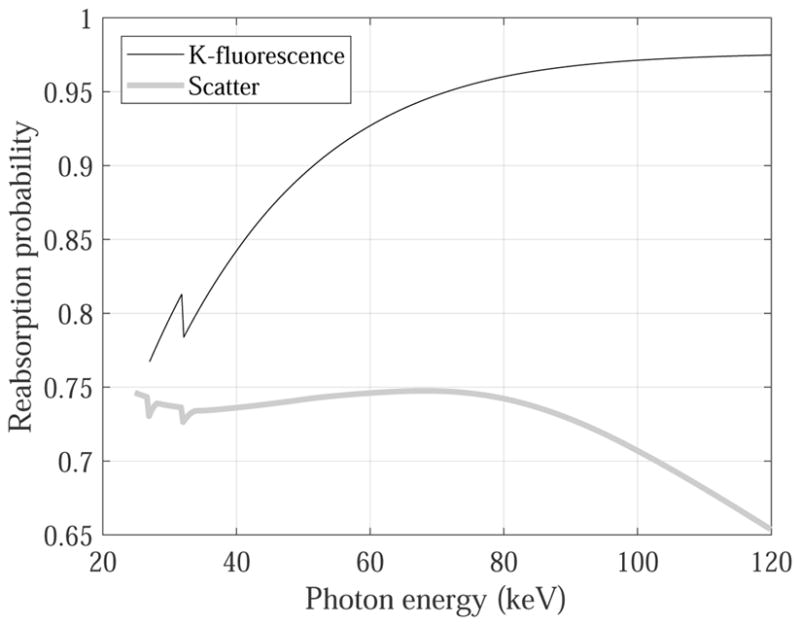
Calculated reabsorption probability of the K-fluorescence and scattered photons at different x-ray energy levels.
The two remaining parameters are the charge spreading radius re used in equation (12), and ACS-induced distance reduction factor κ used in equations (28)–(29). re is strongly influenced by the voltage applied across the CdTe layer, while the value of κ is related to the ACS architecture. However, this information is not provided by the PCD manufacturer. Therefore, the following experimental method was developed to estimate re and κ:
An americium (Am)-241 radioisotope was used as the photon source of the PCD. Activity and half-life of this radioisotope were 10 μCi and 432 years, respectively. When this radioisotope was placed directly at the detector surface during the experiment, the input photon flux was approximately 1 × 104 mm−2s−1. The input and output count rate of the PCD is related by (Knoll 2010)
| (39) |
where n̄in and n̄out are the input and output count rate per pixel respectively, and τ is the detector dead time. As shown in table 2, the PCD used in this work has a dead time smaller than 1 μs for both ACS and single pixel mode. As a result, count rate loss associated with the finite detector dead time, namely the likelihood of pulse pileup, is
| (40) |
Therefore, the Am-241 source led to negligible pulse pileup for the PCD system used in this work.
During the radioisotope-based experiments, the energy threshold of the PCD was adjusted from 22 to 60 keV with a uniform step size of 1.4 keV. Since the lowest threshold (22 keV) was well above the energy level of the 14 keV γ rays emitted from Am-241, the PCD primarily captured other γ rays peaked at 59.5 keV. This information (E = 59.5 keV) was utilized as one of the input parameters in determining re and κ. At this energy level, the x-ray absorption efficiency ε of 2 mm CdTe is approximately 1 (>0.999). Therefore, the term ε in the DQE(0) formula in equation (2) was not considered when implementing the theoretical model.
At each threshold level, 1000 images were recorded using the single pixel mode. From these 1000 images, 100 images were randomly selected, and m̄ and were measured using the method described in (Michel et al. 2006). The method basically traces how many “count clusters” (figure 5) were recorded in the PCD images. Non-zero pixels separated by greater than 250 μm were considered to originate from different input photons, since 250 μm is much greater than the mean travel distance of K-fluorescence photons listed in table 2. For each cluster, the number of non-zero pixels forming the cluster was recorded and denoted as mi, from which the first and second moment of multiplicity were calculated as
Figure 5.

An example 120 × 120 region-of-interest in an image recorded during the radioisotope-based experiments. Black dots indicate triggered pixels, and dashed circles indicate pixel clusters.
| (41) |
and
| (42) |
respectively. Here Nint denotes the total number of photon interactions, and Nc denotes the number of clusters. At each threshold level, Nc was determined by counting the number of pixel clusters as shown in figure 5. In comparison, Nint was fixed across different threshold levels; its value was estimated based on the number of clusters measured at the lowest threshold (22 keV) and with ACS. Under this condition, a 59.5 keV photon was assumed to trigger at least one pixel. With the measured m̄ and , the experimental DQE(0) was obtained based on equation (2). The measurement process was repeated 10 times, each processing 100 randomly selected images. The error bars of the measured m̄, , and DQE(0) were determined by calculating the standard deviations across the 10 repeated measurements.
Additionally, the theoretical models of m̄, , and DQE(0) were implemented based on the procedure described in section 3.3, except that re was kept as an adjustable parameter. The theoretical and experimental m̄, , and DQE(0) were compared at all threshold levels; the value of re was determined by minimizing the sum of squared errors.
After determining the value of re under the single pixel mode, the experiments were repeated under the ACS mode, and the theoretical model was re-implemented with κ as the only adjustable parameter. The experimental and theoretical DQE(0) values were compared, and the value of κ was determined by minimizing the summation of squared errors across all thresholds.
3.3. Numerical implementation of the theoretical model
To be more specific about the numerical implementation method of the theoretical model, a step-by-step guide is provided as follows
For a given x-ray energy E, calculate ε based on equation (3) and thickness (D) of CdTe.
Based on E, W and equations (7)–(9), calculate q̄2.
Divide each l×l detector pixel into 100×100 sub-pixels to get Δa, then calculate q̄3(x, y|0, 0) and using q̄2, Δa and equations (12)–(16). Use (0, 0) for (xi, yi).
From q̄3(x, y|0, 0) and , calculate using equation (18).
Calculate σq5 (x, y, 0, 0) based on σq4 (x, y|0, 0) and equation (20), where the integration was implemented as summation (over the 100 × 100 sub-pixels).
Calculate q̄6(x, y|0, 0) and from and σ6 using equations (21)–(22).
Based on the charge cloud radius re, implement function G(x, y|0, 0)re defined in Appendix A.
-
Calculate from G(x, y|0, 0)re (j = a, b, c):
Equation (A.1) for path a and c;
Equation (A.3) for path b.
Use equation (27) to calculate from , and qt.
Calculate m̄j(qt, E) and from using equations (30)–(31).
Calculate for the three parallel paths using equations (4)–(6).
Calculate m̄PE(qt, E) and from and using equations (32)–(33).
Repeat Steps (ii)–(xii), except replace E by the scattered photon energy Es to obtain and .
Calculate m̄(qt, E) and based on equations (36)–(37).
For polychromatic radiation, repeat Steps (i)–(xiv) for different E levels, then calculate the DQE(0) based on equation (38) and the x-ray spectrum.
3.4. Validation of the theoretical model
To validate the theoretical model, experiments that were independent from those in section 3.2 were performed. A rotating-anode diagnostic x-ray tube (G-1592 with B- 180H housing, Varian Medical Systems, Inc. Salt Lake City, UT) served as the x-ray source of the PCD. The tube was powered by a 80 kW high frequency generator (Indico 100, CPI Inc., Georgetown, Ontario, Canada), and it was operated at four tube potentials ranging from 50 to 120 kV. Each polychromatic beam was collimated to a 3×3 cm2 area (measured at the detector surface) to reduce scattering by air. External filtration and mean beam energies, as well as tube current and energy thresholds used for each beam, are listed in table 3. Based on the entrance flux rate listed in table 3 and equation (39), the pulse pileup effect was found to be negligible. For each beam, and at each energy threshold level, 1000 images were recorded, and the DQE(0) was experimentally measured using the method reported in (Michel et al. 2006). This method has been briefly described in section 3.2.
Table 3.
Parameters of the four polychromatic x-ray beams used in the experimental validation study.
| kVp | 50 | 70 | 90 | 120 |
|---|---|---|---|---|
| Added filtration (mm Cu) | 2 | 4 | 4 | 4 |
| Tube current (mA) | 15 | 15 | 10 | 2 |
| Mean energy (keV) | 45 | 63 | 76 | 93 |
| X-ray flux at detector surface (mm−2s−1) | 10 | 8.6 × 103 | 7.3 × 104 | 9.3 × 104 |
| Detector readout time per image (μs) | 5000 | 5 | 1 | 1 |
| Lowest energy threshold (keV) | 17 | 17 | 17 | 18 |
| Highest energy threshold (keV) | 50 | 70 | 80 | 80 |
| Threshold step (keV) | 2.8 | 3.5 | 2.1 | 4.1 |
The experimental m̄, and DQE(0) were compared with those provided by the theoretical model. In the following Results section, the error of the theoretical model (theoretical - experimental) was provided for every beam and threshold level tested to facilitate readers in evaluating both the global and local accuracy of the model.
4. Results
4.1. Parameters of the theoretical model
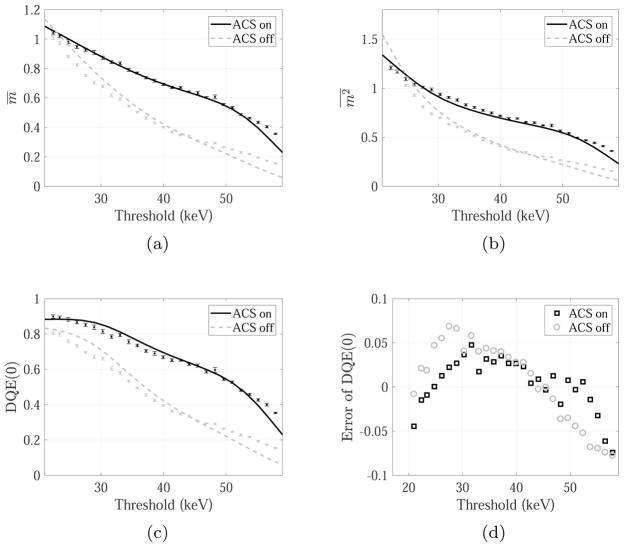
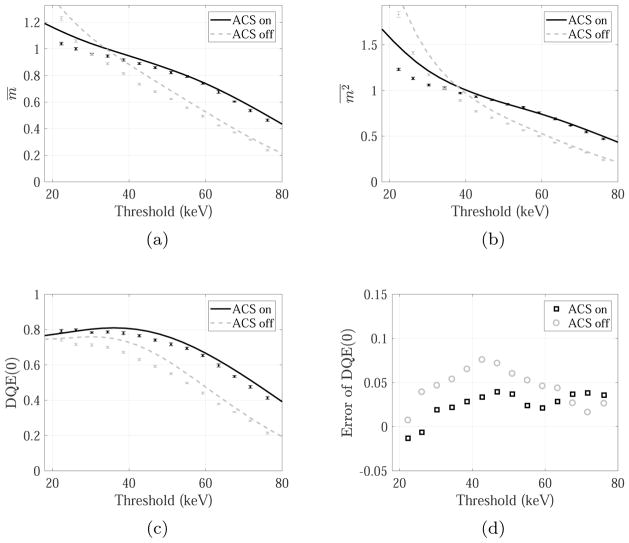
Experimental results measured with the Am-241 radioisotope are shown in figure 6. Values of the two model parameters (re and κ) were determined from these radioisotope-based results (table 4). Once these two parameters were determined, they were fixed for all other experimental studies.
Figure 6.
m̄, and DQE(0) measured with the Am-241 isotope. Discrete data points with error-bars represent experimental data (black: with ACS; gray: without ACS), and they were used to determine the values of re and κ listed in table 4. The corresponding theoretical results are shown as solid (with ACS) and dashed line (without ACS).
Table 4.
Values of charge cloud radius (re) and ACS distance reduction factor (κ) determined from the Am-241-based experiments.
| Charge cloud radius (μm) | 13 |
| ACS distance reduction factor κ | 0.4 |
4.2. Validation of the theoretical model
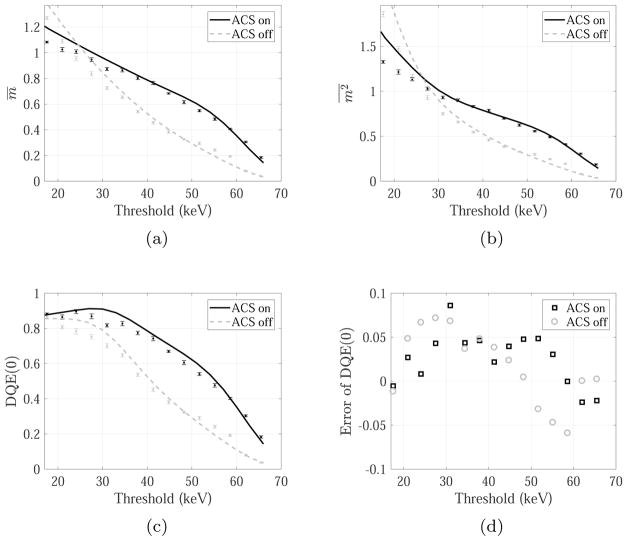
The experimental m̄, , and DQE(0) measured with the four polychromatic x-ray beams are shown in figures 7–10. The corresponding theoretical values and errors are also shown in these figures. With the exception of the 50 kVp beam, ACS decreased the mean value of multiplicity (m̄) at relatively small threshold levels, since shared charge could easily generate detector counts at low threshold under the single pixel mode, and the use of ACS reassigned these shared charges to a central pixel thus reducing multiplicity. At larger threshold levels, it became increasing difficult for any of the shared charge to generate detector counts under the single pixel mode, and the use of ACS summed those shared charges together and made the generation of each count easier. For the low energy 50 kVp beam, due to the relatively low energy of input photon, it is difficult for the shared charge to generate counts in the single pixel mode even at the lowest threshold, therefore ACS always increases m̄.
Figure 7.
Experimental m̄, and DQE(0) measured with the 50 kVp polychromatic beam. Solid and dashed line represent theoretical values with and without ACS, respectively. Discrete data points with errorbars represent experimental data.
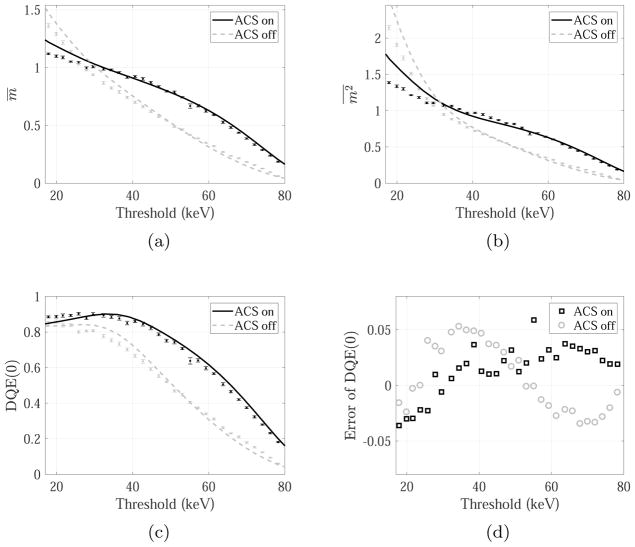
Figure 10.
Experimental and theoretical m̄, and DQE(0) for the 120 kVp polychromatic beam.
Unlike m̄, intuitive understanding of the dependence of on threshold and beam energy is more difficult to obtain, and this is where one may find the proposed theoretical model useful. As shown in figures 7–10, implementation of the model provided values that are representative of the dependence of on energy threshold and ACS: except the 50 kVp beam, the ACS decreased at low threshold and increased at higher thresholds. For the 50 kVp beam, ACS almost always increased . Theoretical has the best agreement with the experimental value at thresholds above 35 keV; at lower thresholds, the theory tends to overestimate . For both ACS and single pixel modes, the overall trends of the theoretical and experimental -threshold curves are matched.
Figures 7–10 also show that the DQE(0) of the PCD is always improved by ACS at the tested threshold levels and beam conditions. The largest improvement came at certain intermediate threshold levels (e.g., 40 keV for the 50 kVp beam; 60 keV for the 120 kVp beam). At very low threshold levels such as 20 keV, the difference in the DQE(0) between the ACS and single pixel mode became smaller. For 90% of the DQE(0) data points in figures 7–10, the errors of the theoretical model were within ±0.05. The largest absolute error was 0.09, corresponding to the DQE(0) for the 70 kVp beam with 31 keV threshold and ACS. Compared with the other three beams, the 120 kVp beam led to the highest global error for the theoretical results. For this beam, the theory overestimated the DQE(0) of the single pixel mode by approximately 0.05 (range: [0.01, 0.08]).
5. Discussion
In this work, a new theoretical approach was developed to incorporate ACS into the cascaded systems analysis framework for photon counting detectors. By introducing an effective reduction factor (κ) for the charge cloud radius and K-fluorescence travel distance, the ACS architecture, which often involves multi-level discriminators, charge summation circuitry, and arbitration circuitry, can be treated as a modified version of the conventional single pixel mode that has a reduced charge sharing problem. This new treatment of ACS allows the multiplicity and DQE(0) of a PCD to be theoretically modeled without introducing additional probability density functions to count for the complex sub-processes in ACS.
For most theoretical detector models, determination of model parameters is a challenging task. As another major contribution, this work presents a methodology on how to determine parameters of the proposed model, without the need to perform Monte- Carlo simulations and prior knowledge of the detailed ACS implementation method. All parameters involved in the proposed method were categorized into three groups: (1) parameters (such as those related to the CdTe material properties) that can be directly determined based on published values; (2) parameters (such as the K-fluorescence reabsorption fraction) that can be analytically calculated based on published methods; (3) the remaining two parameters re and κ. Using a quasi-monoenergetic γ-ray source (Am-241), the DQE(0) was experimentally measured at different threshold levels under the single pixel mode, and the value of re was estimated based on the difference between the theoretical and experimental DQE(0). Once re was determined, ACS was turned on and κ was estimated using a similar method.
Validation of the theoretical model was performed under different experimental conditions: First, the photon source used in validation experiments is independent from the γ-ray source. A rotating-anode diagnostic tube that generates polychromatic x-rays was used as the photon source for the validation experiments. For a given tube potential, the x-ray beam was composed of photons with a range of energies. Second, four different tube potentials were used for the validation experiments, covering a wide range of x-ray energies up to 120 keV.
As shown by both the theoretical and experimental results, the impact of ACS to multiplicity depends on x-ray energy and detector threshold level. When a low threshold is applied to a relatively high energy beam, ACS tends to decrease both the first and second moments of multiplicity. For other cases, ACS increases the first and second moments of multiplicity. Meanwhile, as correctly predicted by the theoretical model, ACS always increases DQE(0), even under the condition of low threshold combined with high x-ray energy: in this case, although ACS decreased m̄, it also reduced by a larger fraction, leading to a higher DQE(0) according to equation (2).
Despite the capability of the presented theory in modeling the dependence of multiplicity and DQE(0) on ACS, this work contains the following limitations. First, the models of certain intermediate imaging stages are empirical. For example, lateral spreading of electrons in Stage 3 was modeled using a normal distribution function, and the probability distribution function of q6 was also assumed to be normally distributed. Accuracy of the model may be compromised if the actual physical process significantly deviates from these empirical models. In that case, more realistic models need to be investigated. Second, pulse pileup is not included in the theoretical model. The current model is not directly applicable to cases that require relatively high photon flux. In fact, for the PCD system used in this work, pulse pileup was negligible (<1%) up until 2×106 photons/[mm2s]. For certain clinical CT imaging applications, the required flux may exceed this level, and the theoretical model needs to be modified to take pulse pileup into account. Third, this work does not cover many other aspects of the PCD performance that can be influenced by ACS. For example, inter-pixel communications involved in the ACS process may increase the detector dead time and reduce the maximum count rate of the PCD system (Ullberg et al. 2013), leading to pileup effects at lower photon fluxes. As shown in table 2, for the PCD system used in this work, the dead time was increased from 140 ns under single pixel mode, to 550 ns under ACS mode. It is important to recognize the impacts of ACS to detector dead time, particularly for applications requiring high photon flux. As another example, by correctly re-assigning shared charge to a single primary pixel, ACS could improve the accuracy of the detected photon energy (Ballabriga et al. 2007). Similarly, ACS may also improve the spatial resolution of the PCD by reducing shared charge, particularly when the input x-ray energy is much higher than the energy threshold: in this case, shared charge often contributes to detector count in the single pixel mode (Ullberg et al. 2013), and the use of ACS can reduce the number of detector pixels incorrectly triggered by a single input photon, therefore reducing the spatial spreading of input signal. When the threshold is high enough compared to the x-ray energy so that shared charge is unlikely to generate false detector count, ACS may degrade MTF (Koenig et al. 2014). The complex dependence of spatial resolution on ACS warrants further theoretical modeling, which is a subject of our future work. Other PCD properties not covered by the theoretical analysis in this work include frequency-dependent DQE, noise power spectrum, etc. The use of the ACS mode should take these properties and the nature of the imaging task into account, rather than solely DQE(0)-based. Finally, the accuracy of the theoretical DQE(0) under low threshold and high x-ray energy (e.g., >100 keV) conditions needs to be further improved. Lack of considerations of threshold dispersion and the stochastic nature of the photon interaction depth may contribute to the error of the model. The energy dependence of the charge cloud radius (Donmez et al. 2005) was not considered when implementing the model, which could also degrade the accuracy of the theoretical value. Energy of the recoil electron from Compton scattering was assumed to be smaller than the energy threshold. However, its contribution to multiplicity may no longer be zero at higher x-ray energies.
6. Conclusions
To help understand the impact of ACS to the multiplicity and DQE(0) of CdTe-based PCD system, a theoretical model was developed. Unlike previously reported models, this model does not require prior knowledge of the specific implementation method for ACS, and does not need Monte-Carlo simulations to determine model parameters. It also does not invoke extensive use of the probability density function to model intermediate operations in ACS such as charge summation and arbitration. Experimental validation studies showed that the model can predict the threshold-dependence of multiplicity and DQE(0) for polychromatic x-rays.
Figure 8.
Experimental and theoretical m̄, and DQE(0) for the 70 kVp polychromatic beam.
Figure 9.
Experimental and theoretical m̄, and DQE(0) for the 90 kVp polychromatic beam.
Acknowledgments
This work was partially supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number R01EB020521, and by the Office of the Assistant Secretary of Defense for Health Affairs, through the Breast Cancer Research Program, under Award No. W81XWH-16-1-0031. Opinions, interpretations, conclusions and recommendations are those of the authors; they do not necessarily represent the official views of the National Institutes of Health, and are not necessarily endorsed by the federal funding agencies. The authors are grateful for the editorial assistance from Dalton Griner, Kayla M. Gomez Cardona and Daniel Gomez Cardona. Finally, the authors would like to thank the anonymous reviewers for their comments and suggestions to improve the quality of this paper.
Appendix A: Derivation of q̄7 for photoelectric-only process
Taking path a as an example: For an input photon interaction at location (xi, yi), the following expression provides the expected number of electrons collected within a pixel centered at (x, y)
| (A.1) |
where function G(x, y|xi, yi) has the following analytical form:
| (A.2) |
Equation (A.2) was derived by integrating q̄4 within the l × l pixel area as in equation (19), with the assumption that the spatial spreading of q̄4 in the xy plane follows the normal distribution [as shown in equation (12)]. By combining equation (A.1) with equations (25) and (26), can be calculated.
The derivation of is similar to that of , except that should replace in equation (A.1).
For path b, due to K-fluorescence reabsorption, there is an additional term in the expression of q̄6,
| (A.3) |
where ΔxK and ΔyK denote the travel distance of the K-fluorescence photon along the x and y axis, respectively. Accordingly, The corresponding is denoted as . Due to the stochastic nature of ΔxK and ΔyK, the following averaging process needs to be performed to get the mean value of
| (A.4) |
where Pr(ΔxK,ΔyK) is the probability for the K-fluorescence to travel (ΔxK,ΔyK) from its origin (xi, yi). Based on the first mean value theorem for definite integrals, there exist a pair of Δ̄x, Δ̄y, such that
| (A.5) |
In equation (A.5), Δ̄x and Δ̄y can be considered as the effective path lengths of the K-fluorescence photon along the x and y axis, respectively.
In a three-dimensional (3D) layer of CdTe, the mean travel distance of K-fluorescence photons (denoted as ) can be estimated using the inverse of x-ray linear attenuation coefficient μ. When projecting onto the 2D xy plane, the average value (denoted as Δ̄K) is given by
| (A.6) |
The mean value of Δ̄K, when it is projected onto the x axis, is given by
| (A.7) |
The value of Δ̄yK is the same as Δ̄xK. By putting Δ̄xK and Δ̄yK back to equations (A.4)–(A.5), q̄7 of path b can be calculated. Since x ray-CdTe interactions can generate four major types of K-fluorescence photons (Kα of Cd, Kβ of Cd, Kα of Te, Kβ of Te), the calculation q̄7 was performed separately for each type of K-fluorescence based on the four Δ̄K values listed in table 2, then the average q̄7 was calculated according to their relative likelihoods listed in table 1.
Appendix B: Derivation of m̄ and for photoelectric-only paths
For an interacted photon going through a given path (a, b, c) of a PE-only process, it can generate either one or zero count at a detector pixel (u, v), where (u, v) denotes the index of the pixel centered at (x = ul, y = vl). For this pixel, the likelihood of registering 1 count is
| (B.1) |
and the likelihood for this pixel to registering 0 count is
| (B.2) |
Based on equations (B.1)–(B.2), for a given set of (qt, xi, yi, E) and a given path, the expected output of pixel (u, v) is
| (B.3) |
| (B.4) |
By definition, the detector multiplicity for a given set of (qt, xi, yi, E) and a given path is
| (B.5) |
Based on equation (B.3), its first moment is given by
| (B.6) |
Similarly, the second moment of m is given by
| (B.7) |
| (B.8) |
| (B.9) |
In deriving the intermediate step (B.8) from (B.7), the property of was used based on very weak noise correlation found in CdTe-based PCD (Ullberg et al. 2013).
Equations (B.6) and (B.9) provide formulas of m̄ and for a given interaction position (xi, yi). The next step is to take the corresponding average over all the possible input position, namely
| (B.10) |
where Pr(xi, yi) is the probability density distribution for the input photon location. When the pixel size is much smaller than the total detector area, m̄(xi, yi) can be considered as a 2D periodic function with a period of l along the x and y direction. As long as the input photon beam is uniform within a pixel area, Pr(xi, yi) = 1/l2, and equation (B.10) becomes
| (B.11) |
| (B.12) |
| (B.13) |
where the derivation from (B.11) to (B.12) assumed shift invariance of q̄7.
Similarly, is given by
| (B.14) |
The formulas of m̄ and derived in Appendix B are applicable to each of the three paths (a, b, c). The joint contribution of the three paths to multiplicity is provided in equations (32)–(33) in section 2.8.
Appendix C: Derivation of m̄ and for paths starting with scattering
For the specific purpose of multiplicity modeling, a process starting with x-ray scattering can be considered as a modified photoelectric process, in which the input x-ray energy is reduced from E to Es. Once scattered, the photon could interact again with CdTe through any of the three paths (a, b, c). For a given threshold qt and scattered photon with energy Es, to derive the m̄ and of scattering-initiated process, one needs to take the average over the input position (xi, yi), then combine the expected multiplicity of the three photoelectric-only processes, and finally take the average over the traveling distance of the scattered photon (Δxs,Δys):
| (C.1) |
where j ∈ [a, b, c] denotes the index of the three photoelectric-only paths, Pr(Δxs,Δys) is the probability distribution for the scattered photon to travel by (Δxs,Δys). The integral over (xi, yi) given by
| (C.2) |
| (C.3) |
| (C.4) |
where m̄j is calculated using equation (B.13), with the exception that Es replaces E. In deriving (C.3) from (C.2), the periodic property of m̄s was utilized. As shown in equation (C.4), the result of the integral over (xi, yi) actually has no dependence on (Δxs,Δys). Therefore, equation (C.1) can be simplified to
| (C.5) |
Therefore, for a given detector threshold level qt, the mean multiplicity of photons scattered by CdTe is equal to that of photons with initial energy Es going through the PE-only processes.
Using similar analysis, it can be shown that, for a given qt level,
| (C.6) |
Appendix D: DQE(0) of PCD with polychromatic radiation
For a given interacted photon and a given PCD threshold level (qt), a detector count could be registered in one or multiple pixels; in cases such as the escape of the incoherently scattered photon, or if photon energy E is well below qt, there could also be no pixel responding to a photon interaction. The multiplicity m defines the number of pixels registering counts from a single interacted photon, and its first moment is given by
| (D.1) |
For a polychromatic beam, the input photons may have different energies. As shown in this paper, the probability of getting m counts from an input photon, namely Pr(m), depends on the x-ray energy E. In this case, the probability density function of photon energy needs to be considered
| (D.2) |
| (D.3) |
| (D.4) |
where
| (D.5) |
is given in equation (36). From equation (D.2) to (D.3), the convention of using the symbol Ω(E) to denote Pr(E), namely the x-ray spectrum, was employed.
Similarly, for a given qt level, is given by
| (D.6) |
| (D.7) |
where
| (D.8) |
is given in equation (37).
With polychromatic radiation, the term ε in the DQE(0) formula in equation (2) is given by
| (D.9) |
Based on equations (D.4), (D.7), and (D.9), the general PCD DQE(0) formula in equation (2) can be expressed in terms of Ω(E), m̄(E), and as
| (D.10) |
for a given threshold (qt) level.
References
- Ballabriga R, Alozy J, Blaj G, Campbell M, Fiederle M, Frojdh E, Heijne EHM, Llopart X, Pichotka M, Procz S, Tlustos L, Wong W. The Medipix3RX: a high resolution, zero dead-time pixel detector readout chip allowing spectroscopic imaging. J Instrum. 2013;8(02):C02016. [Google Scholar]
- Ballabriga R, Alozy J, Campbell M, Frojdh E, Heijne E, Koenig T, Llopart X, Marchal J, Pennicard D, Poikela T, Tlustos L, Valerio P, Wong W, Zuber M. Review of hybrid pixel detector readout ASICs for spectroscopic X-ray imaging. J Instrum. 2016;11(01):P01007. [Google Scholar]
- Ballabriga R, Campbell M, Heijne EHM, Llopart X, Tlustos L. The Medipix3 prototype, a pixel readout chip working in single photon counting mode with improved spectrometric performance. IEEE Trans Nucl Sci. 2007;54(5):1824–1829. [Google Scholar]
- Barradas NP, Reis MA. Accurate calculation of pileup effects in pixe spectra from first principles. X Ray Spectrom. 2006;35(4):232–237. [Google Scholar]
- Barrett HH, Eskin JD, Barber HB. Charge transport in arrays of semiconductor gamma-ray detectors. Phys Rev Lett. 1995;75:156–159. doi: 10.1103/PhysRevLett.75.156. [DOI] [PubMed] [Google Scholar]
- Bissonnette JP, Cunningham IA, Jaffray DA, Fenster A, Munro P. A quantum accounting and detective quantum efficiency analysis for video-based portal imaging. Med Phys. 1997;24(6):815–826. doi: 10.1118/1.598009. [DOI] [PubMed] [Google Scholar]
- Chmeissani M, Mikulec B. Performance limits of a single photon counting pixel system. Nucl Instrum Meth A; Proc. 1st Int. Workshop on Radiation Imaging Detectors.2001. pp. 81–90. [Google Scholar]
- Cunningham IA. Linear-systems modeling of parallel cascaded stochastic processes: the NPS of radiographic screens with reabsorption of characteristic x-radiation. Proc SPIE. 1998;3336:220–230. [Google Scholar]
- Cunningham IA, Westmore MS, Fenster A. A spatial-frequency dependent quantum accounting diagram and detective quantum efficiency model of signal and noise propagation in cascaded imaging systems. Med Phys. 1994;21(3):417–427. doi: 10.1118/1.597401. [DOI] [PubMed] [Google Scholar]
- Donmez B, Macri JR, McConnell ML, Ryan JM, Widholm M, Hamel LA, Narita T. IEEE Nucl Sci Symp Conf Rec (2005) 2005;3:1408–1411. [Google Scholar]
- Drake DG, Jaffray DA, Wong JW. Characterization of a fluoroscopic imaging system for kV and MV radiography. Med Phys. 2000;27(5):898–905. doi: 10.1118/1.598955. [DOI] [PubMed] [Google Scholar]
- Fano U. Ionization yield of radiations. ii the fluctuations of the number of ions. Phys Rev. 1947;72:26–29. [Google Scholar]
- Feuerlein S, Roessl E, Proksa R, Martens G, Klass O, Jeltsch M, Rasche V, Brambs HJ, Hoffmann MHK, Schlomka JP. Multienergy photon-counting K-edge imaging: Potential for improved luminal depiction in vascular imaging. Radiology. 2008;249(3):1010–1016. doi: 10.1148/radiol.2492080560. [DOI] [PubMed] [Google Scholar]
- Gang GJ, Lee J, Stayman JW, Tward DJ, Zbijewski W, Prince JL, Siewerdsen JH. Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance. Med Phys. 2011;38:1754. doi: 10.1118/1.3560428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gang GJ, Stayman JW, Zbijewski W, Siewerdsen JH. Task-based detectability in CT image reconstruction by filtered backprojection and penalized likelihood estimation. Med Phys. 2014;41(8):081902. doi: 10.1118/1.4883816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly A, Rudin S, Bednarek DR, Hoffmann KR. Micro-angiography for neuro-vascular imaging. II cascade model analysis. Med Phys. 2003;30(11):3029–3039. doi: 10.1118/1.1617550. [DOI] [PubMed] [Google Scholar]
- Ge Y, Ji X, Zhang R, Li K, Chen GH. K-edge energy-based calibration method for photon counting detectors. Phys Med Biol. 2018;63(1):015022. doi: 10.1088/1361-6560/aa9637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge Y, Zhang R, Li K, Chen GH. Improving radiation dose efficiency of x-ray differential phase contrast imaging using an energy-resolving grating interferometer and a novel rank constraint. Opt Express. 2016;24(12):12955–12968. doi: 10.1364/OE.24.012955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gimenez E, Maneuski D, Raighne AM, Parkes C, Bates R, Shea VO, Fleta C, Pellegrini G, Lozano M, Alianelli L, Sawhney K, Marchal J, Tartoni N. 3D Medipix2 detector characterization with a micro-focused x-ray beam. Nucl Instrum Meth A. 2011a;633(Supplement 1):S114–S116. [Google Scholar]
- Gimenez EN, Ballabriga R, Campbell M, Horswell I, Llopart X, Marchal J, Sawhney KJS, Tartoni N, Turecek D. Characterization of Medipix3 with synchrotron radiation. IEEE Trans Nucl Sci. 2011b;58(1):323–332. [Google Scholar]
- Hamann E, Koenig T, Zuber M, Cecilia A, Tyazhev A, Tolbanov O, Procz S, Fauler A, Baumbach T, Fiederle M. Performance of a medipix3rx spectroscopic pixel detector with a high resistivity gallium arsenide sensor. IEEE Trans Med Imag. 2015;34(3):707–715. doi: 10.1109/TMI.2014.2317314. [DOI] [PubMed] [Google Scholar]
- Iwanczyk JS, Nygard E, Meirav O, Arenson J, Barber WC, Hartsough NE, Malakhov N, Wessel JC. Photon counting energy dispersive detector arrays for x-ray imaging. IEEE Trans Nucl Sci. 2009;56(3):535–542. doi: 10.1109/TNS.2009.2013709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwanczyk J, Szymczyk W, Traczyk M, Triboulet R. X-ray fluorescence escape peaks in gamma-ray spectra detected by CdTe detectors. Nucl Instrum Meth. 1979;165(2):289–295. [Google Scholar]
- Ji X, Zhang R, Ge Y, Chen GH, Li K. Signal and noise characteristics of a CdTe-based photon counting detector: cascaded systems analysis and experimental studies. Proc SPIE. 2017;10132:1013207–1013207-6. doi: 10.1117/12.2255063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johns PC, Yaffe MJ. Correction of pulse-height spectra for peak pileup effects using periodic and random pulse generators. Nucl Instrum Meth A. 1987;255(3):559–581. [Google Scholar]
- Jone RC. Advances in Electronics and Electron Physics. Vol. 11. Academic Press; 1959. pp. 87–183. [Google Scholar]
- Knoll GF. Radiation Detection and Measurement. 4. Wiley; 2010. [Google Scholar]
- Koenig T, Hamann E, Procz S, Ballabriga R, Cecilia A, Zuber M, Llopart X, Campbell M, Fauler A, Baumbach T, Fiederle M. Charge summing in spectroscopic x-ray detectors with high-Z sensors. IEEE Trans Nucl Sci. 2013;60(6):4713–4718. [Google Scholar]
- Koenig T, Zuber M, Hamann E, Cecilia A, Ballabriga R, Campbell M, Ruat M, Tlustos L, Fauler A, Fiederle M, Baumbach T. How spectroscopic x-ray imaging benefits from inter-pixel communication. Phys Med Biol. 2014;59(20):6195. doi: 10.1088/0031-9155/59/20/6195. [DOI] [PubMed] [Google Scholar]
- Lee Y, Lee S, Kim HJ. Comparison of spectral CT imaging methods based a photon-counting detector: Experimental study. Nucl Instrum Meth A. 2016;815:68–74. [Google Scholar]
- Leng S, Yu Z, Halaweish A, Kappler S, Hahn K, Henning A, Li Z, Lane J, Levin DL, Jorgensen S, Ritman E, McCollough C. A high-resolution imaging technique using a whole-body, research photon counting detector CT system. Proc SPIE. 2016;9783:97831I-97831I–6. doi: 10.1117/12.2217180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Bevins N, Zambelli J, Chen GH. Fundamental relationship between the noise properties of grating-based differential phase contrast CT and absorption CT: Theoretical framework using a cascaded system model and experimental validation. Med Phys. 2013;40(2):021908. doi: 10.1118/1.4788647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Chen GH. Noise characteristics of CT perfusion imaging: how does noise propagate from source images to final perfusion maps? Proc SPIE. 2016;9783:978310. doi: 10.1117/12.2216293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandel L. Image fluctuations in cascade intensifiers. Br J Appl Phys. 1959;10(5):233. [Google Scholar]
- Marchal J. Theoretical analysis of the effect of charge-sharing on the detective quantum efficiency of single-photon counting segmented silicon detectors. J Instrum. 2010;5(01):P01004. [Google Scholar]
- Matz R, Weidner M. Charge collection efficiency and space charge formation in CdTe gamma and X-ray detectors. Nucl Instrum Meth A. 1998;406:287–298. [Google Scholar]
- Michel T, Anton G, Bohnel M, Durst J, Firsching M, Korn A, Kreisler B, Loehr A, Nachtrab F, Niederlohner D, Sukowski F, Talla PT. A fundamental method to determine the signal-to-noise ratio (SNR) and detective quantum efficiency (DQE) for a photon counting pixel detector. Nucl Instrum Meth A. 2006;568(2):799–802. [Google Scholar]
- Owens A, Peacock A. Compound semiconductor radiation detectors. Nucl Instrum Meth A; Proceedings of the 5th International Workshop on Radiation Imaging Detectors.2004. pp. 18–37. [Google Scholar]
- Pelzer G, Weber T, Anton G, Ballabriga R, Bayer F, Campbell M, Gabor T, Haas W, Horn F, Llopart X, Michel N, Mollenbauer U, Rieger J, Ritter A, Ritter I, Sievers P, Wölfel S, Wong WS, Zang A, Michel T. Grating-based x-ray phase-contrast imaging with a multi energy-channel photon-counting pixel detector. Opt Express. 2013;21(22):25677–25684. doi: 10.1364/OE.21.025677. [DOI] [PubMed] [Google Scholar]
- Pennicard D, Ballabriga R, Llopart X, Campbell M, Graafsma H. Simulations of charge summing and threshold dispersion effects in Medipix3. Nucl Instrum Meth A. 2011;636(1):74–81. [Google Scholar]
- Pennicard D, Marchal J, Fleta C, Pellegrini G, Lozano M, Parkes C, Tartoni N, Barnett D, Dolbnya I, Sawhney K, Bates R, O’Shea V, Wright V. Synchrotron tests of a 3D Medipix2 x-ray detector. IEEE Trans Nucl Sci. 2010;57(1):387–394. [Google Scholar]
- Prakash P, Zbijewski W, Gang GJ, Ding Y, Stayman JW, Yorkston J, Carrino JA, Siewerdsen JH. Task-based modeling and optimization of a cone-beam CT scanner for musculoskeletal imaging. Med Phys. 2011;38(10):5612–5629. doi: 10.1118/1.3633937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabbani M, Shaw R, Metter RV. Detective quantum efficiency of imaging systems with amplifying and scattering mechanisms. J Opt Soc Am A. 1987;4(5):895–901. doi: 10.1364/josaa.4.000895. [DOI] [PubMed] [Google Scholar]
- Redus RH, Pantazis JA, Pantazis TJ, Huber AC, Cross BJ. Characterization of CdTe detectors for quantitative x-ray spectroscopy. IEEE Trans Nucl Sci. 2009;56(4):2524–2532. [Google Scholar]
- Richard S, Siewerdsen JH. Cascaded systems analysis of noise reduction algorithms in dual-energy imaging. Med Phys. 2008;35(2):586–601. doi: 10.1118/1.2826556. [DOI] [PubMed] [Google Scholar]
- Rink K, Oelfke U, Fiederle M, Zuber M, Koenig T. Investigating the feasibility of photon-counting K-edge imaging at high x-ray fluxes using nonlinearity corrections. Med Phys. 2013;40(10):101908. doi: 10.1118/1.4820535. [DOI] [PubMed] [Google Scholar]
- Roessl E, Brendel B, Engel KJ, Schlomka JP, Thran A, Proksa R. Sensitivity of photon-counting based K-edge imaging in x-ray computed tomography. IEEE Trans Med Imag. 2011;30(9):1678–1690. doi: 10.1109/TMI.2011.2142188. [DOI] [PubMed] [Google Scholar]
- Russo P, Del Guerra A. Springer; New York New York, NY: 2014. pp. 23–82. [Google Scholar]
- Sato E, Oda Y, Abudurexiti A, Hagiwara O, Matsukiyo H, Osawa A, Enomoto T, Watanabe M, Kusachi S, Sato S, Ogawa A, Onagawa J. Demonstration of enhanced iodine K-edge imaging using an energy-dispersive x-ray computed tomography system with a 25 mm/s-scan linear cadmium telluride detector and a single comparator. Appl Radiat Isot. 2012;70(5):831–836. doi: 10.1016/j.apradiso.2012.02.007. [DOI] [PubMed] [Google Scholar]
- Schlomka JP, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, Bumer C, Herrmann C, Steadman R, Zeitler G, Livne A, Proksa R. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Phys Med Biol. 2008;53(15):4031. doi: 10.1088/0031-9155/53/15/002. [DOI] [PubMed] [Google Scholar]
- Schmidt TG. Optimal ”image-based” weighting for energy-resolved CT. Med Phys. 2009;36(7):3018–3027. doi: 10.1118/1.3148535. [DOI] [PubMed] [Google Scholar]
- Shikhaliev PM. Energy-resolved computed tomography: first experimental results. PHys Med Biol. 2008;53(20):5595. doi: 10.1088/0031-9155/53/20/002. [DOI] [PubMed] [Google Scholar]
- Shikhaliev PM, Fritz SG. Photon counting spectral CT versus conventional CT: comparative evaluation for breast imaging application. Phys Med Biol. 2011;56(7):1905. doi: 10.1088/0031-9155/56/7/001. [DOI] [PubMed] [Google Scholar]
- Shikhaliev PM, Fritz SG, Chapman JW. Photon counting multienergy x-ray imaging: Effect of the characteristic x rays on detector performance. Med Phys. 2009;36(11):5107–5119. doi: 10.1118/1.3245875. [DOI] [PubMed] [Google Scholar]
- Shockley W, Pierce JR. A theory of noise for electron multipliers. Proc IRE. 1938;26(3):321–332. [Google Scholar]
- Siewerdsen J, Antonuk L, El-Mohri Y, Yorkston J, Huang W, Cunningham I. Signal, noise power spectrum, and detective quantum efficiency of indirect-detection flat-panel imagers for diagnostic radiology. Med Phys. 1998;25:614. doi: 10.1118/1.598243. [DOI] [PubMed] [Google Scholar]
- Siewerdsen JH, Antonuk LE, El-Mohri Y, Yorkston J, Huang W, Boudry JM, Cunningham IA. Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology. Med Phys. 1997;24(1):71–89. doi: 10.1118/1.597919. [DOI] [PubMed] [Google Scholar]
- Sultana A, Karim KS, Rowlands JA. The effect of k-fluorescence reabsorption of selenium on the performance of an imaging detector for protein crystallography. Phys Status Solidi C. 2009;6(S1):S231–S235. [Google Scholar]
- Symons R, Krauss B, Sahbaee P, Cork TE, Lakshmanan MN, Bluemke DA, Pourmorteza A. Photon-counting CT for simultaneous imaging of multiple contrast agents in the abdomen: An in vivo study. Med Phys. 2017 doi: 10.1002/mp.12301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taguchi K, Frey EC, Wang X, Iwanczyk JS, Barber WC. An analytical model of the effects of pulse pileup on the energy spectrum recorded by energy resolved photon counting x-ray detectors. Med Phys. 2010;37(8):3957–3969. doi: 10.1118/1.3429056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taguchi K, Iwanczyk JS. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Med Phys. 2013;40(10):100901. doi: 10.1118/1.4820371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taguchi K, Zhang M, Frey EC, Wang X, Iwanczyk JS, Nygard E, Hartsough NE, Tsui BMW, Barber WC. Modeling the performance of a photon counting x-ray detector for CT: Energy response and pulse pileup effects. Med Phys. 2011;38(2):1089–1102. doi: 10.1118/1.3539602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanguay J, Yun S, Kim HK, Cunningham IA. The detective quantum efficiency of photon-counting x-ray detectors using cascaded-systems analyses. Med Phys. 2013;40(4):041913. doi: 10.1118/1.4794499. [DOI] [PubMed] [Google Scholar]
- Tanguay J, Yun S, Kim HK, Cunningham IA. Detective quantum efficiency of photon-counting x-ray detectors. Med Phys. 2015;42(1):491–509. doi: 10.1118/1.4903503. [DOI] [PubMed] [Google Scholar]
- Thompson AC, Attwood DT, et al. X-ray Data Booklet. 2. Lawrence Berkeley National Laboratory; Berkeley, California 94720: 2001. [Google Scholar]
- Thuering T, Barber WC, Seo Y, Alhassen F, Iwanczyk JS, Stampanoni M. Energy resolved x-ray grating interferometry. Appl Phys Lett. 2013;102(19):191113. [Google Scholar]
- Tward DJ, Siewerdsen JH. Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT. Med Phys. 2008;35(12):5510–5529. doi: 10.1118/1.3002414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tward DJ, Siewerdsen JH. Noise aliasing and the 3D NEQ of flat-panel cone-beam CT: Effect of 2D/3D apertures and sampling. Med Phys. 2009;36(8):3830–3843. doi: 10.1118/1.3166933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullberg C, Urech M, Weber N, Engman A, Redz A, Henckel F. Measurements of a dual-energy fast photon counting CdTe detector with integrated charge sharing correction. Proc SPIE. 2013;8668:86688. [Google Scholar]
- Veale MC, Bell SJ, Duarte DD, Schneider A, Seller P, Wilson MD, Iniewski K. Measurements of charge sharing in small pixel CdTe detectors. Nucl Instrum Meth A. 2014;767:218–226. [Google Scholar]
- Vedantham S, Karellas A, Suryanarayanan S. Solid-state fluoroscopic imager for high-resolution angiography: Parallel-cascaded linear systems analysis. Med Phys. 2004;31(5):1258–1268. doi: 10.1118/1.1689014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Meier D, Taguchi K, Wagenaar DJ, Patt BE, Frey EC. Material separation in x-ray CT with energy resolved photon-counting detectors. Med Phys. 2011;38(3):1534–1546. doi: 10.1118/1.3553401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wielopolski L, Gardner RP. Prediction of the pulse-height spectral distortion caused by the peak pile-up effect. Nucl Instrum Meth. 1976;133(2):303–309. [Google Scholar]
- Xu J, Zbijewski W, Gang G, Stayman JW, Taguchi K, Lundqvist M, Fredenberg E, Carrino JA, Siewerdsen JH. Cascaded systems analysis of photon counting detectors. Med Phys. 2014;41(10):101907. doi: 10.1118/1.4894733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao J, Cunningham IA. Parallel cascades: New ways to describe noise transfer in medical imaging systems. Med Phys. 2001;28(10):2020–2038. doi: 10.1118/1.1405842. [DOI] [PubMed] [Google Scholar]
- Yu L, Li Z, Leng S, McCollough CH. Dual-source multi-energy CT with triple or quadruple x-ray beams. Proc SPIE. 2016;9783:978312. doi: 10.1117/12.2217446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Z, Leng S, Jorgensen SM, Li Z, Gutjahr R, Chen B, Halaweish AF, Kappler S, Yu L, Ritman EL, McCollough CH. Evaluation of conventional imaging performance in a research whole-body CT system with a photon-counting detector array. Phys Med Biol. 2016;61(4):1572. doi: 10.1088/0031-9155/61/4/1572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Ji WG, Rowlands JA. Effects of characteristic x rays on the noise power spectra and detective quantum efficiency of photoconductive x-ray detectors. Med Phys. 2001;28(10):2039–2049. doi: 10.1118/1.1405845. [DOI] [PubMed] [Google Scholar]
- Zweig HJ. Detective quantum efficiency of photodetectors with some amplification mechanisms. J Opt Soc Am. 1965;55(5):525–528. [Google Scholar]