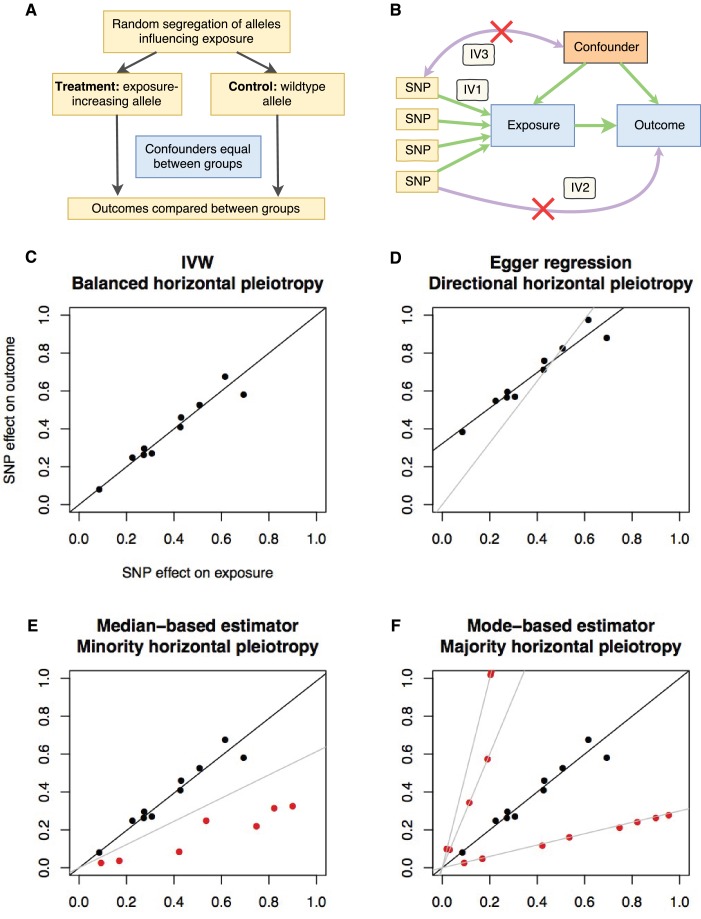
Figure 1. Principles and assumptions behind Mendelian randomization.

(A) Diagram illustrating the analogy between Mendelian randomization (MR) and a randomised controlled trial. (B) A directed acyclic graph representing the MR framework. Instrumental variable (IV) assumption 1: the instruments must be associated with the exposure; IV assumption 2: the instruments must influence the outcome only through the exposure; IV assumption 3: the instruments must not associate with measured or unmeasured confounders. (C-F) Scatter plots demonstrating the relationship between the instrumental single nucleotide polymorphism (SNP) effects on the exposure against their corresponding effects on the outcome. The slope of the regression is the estimate of the causal effect of the exposure on the outcome. (C) If there is no violation of the IV2 assumption (no horizontal pleiotropy), or the horizontal pleiotropy is balanced, an unbiased causal estimate can be obtained by inverse-variance weighted (IVW) linear regression, where the contribution of each instrumental SNP to the overall effect is weighted by the inverse of the variance of the SNP-outcome effect. Fixed and random effects IVW approaches are available (the slopes from both approaches are identical but the variance of the slope is inflated in the random effects model in the presence of heterogeneity between SNPs). (D) If there is a tendency for the horizontal pleiotropic effect to be in a particular direction, then constraining the slope to go through zero will incur bias (grey line). Egger regression relaxes this constraint by allowing the intercept to pass through a value other than zero, returning an unbiased effect estimate if the instrument-exposure and pleiotropic effects are uncorrelated, also known as the InSIDE (Instrument Strength Independent of Direct Effect) assumption (Bowden et al., 2015). Pleiotropic effect here refers to the effect of the instrument on the outcome that is not mediated by the exposure. (E) If the majority of the instruments are valid (black points), with some invalid instruments (red points), the median based approach will provide an unbiased estimate in the presence of unbalanced horizontal pleiotropy (black line), whereas IVW linear regression will provide a biased estimate (grey line). In addition, the median-based estimator does not require the InSIDE assumption of the Egger approach. (F) If a group of SNPs influences the outcome through a particular pathway other than the exposure (i.e. the SNPs are horizontally pleiotropic) then that group of SNPs will return consistently biased estimates. Clustering SNPs based on their estimates (grey lines) is possible with the mode-based estimator. The cluster with the largest weight (black line) is selected as the final causal estimate. The causal estimate from the mode-based estimator is unbiased if the SNPs contributing to the largest cluster are valid instruments.