Spark-MCA: Large-scale, Exhaustive Formal Concept Analysis for Evaluating the Semantic Completeness of SNOMED CT

Abstract

The completeness of a medical terminology system consists of two parts: complete content coverage and complete semantics. In this paper, we focus on semantic completeness and present a scalable approach, called Spark-MCA, for evaluating the semantic completeness of SNOMED CT. We formulate the SNOMED CT contents into an FCA-based formal context, in which SNOMED CT concepts are used for extents, while their attributes are used as intents. We applied Spark-MCA to the 201403 US edition of SNOMED CT to exhaustively compute all the formal concepts and sub concept relationships in about 2 hours with 96 processors using an Amazon Web Service cluster. We found a total of 799,868 formal concepts, within which 500,583 are not contained in the 201403 release. We compared these concepts with the cumulative addition of 22,687 concepts from the 5 “delta” files from the 201403 release to the 201609 release. 3,231 matches were found between those suggested by FCA and those from cumulative concept addition by the SNOMED CT Editorial Panel. This result provides encouraging evidence that our approach could be useful for enhancing the semantic completeness of SNOMED CT.

Introduction

Ontologies (a.k.a. terminology systems) serve as a knowledge source in many biomedical applications including information extraction, information retrieval, data integration, data management, and clinical decision support.¹ The quality of an ontology is a key property that determines its usability. As evidenced by their fast paced evolution (e.g., SNOMED International releases a new version almost every 6 months), ontological systems are often incomplete and under-specified. Therefore, one quality issue is semantic completeness.^2–4 For example, in SNOMED CT, the concept Structure of muscle acting on metatarsophalangeal joint (with identifier 707861009) was not present in the 201403 release but was added in the 201603 release. To study semantic completeness, Jiang and Chute⁴ used Formal Concept Analysis (FCA) as a tool to construct contexts from normal form presentations in SNOMED CT and analyzed the resulting lattice hierarchy for unlabeled nodes. These unlabeled nodes signify semantically incomplete areas in SNOMED CT which can serve as candidate pool of new concepts for inclusion in SNOMED CT.

Given their size and complexity, performing such an FCA-based semantic completeness analysis for large ontologies is computationally as well as methodologically challenging. In fact, constructing concept lattices from formal contexts is believed to be a PSPACE-complete problem. Hence, performing formal concept analysis on large biomedical ontologies in their entirety, such as on SNOMED CT with over 300,000 concepts and 1,360,000 relations, was considered impractical. Because of the computational challenge, Jiang and Chute had to randomly select only 10% of the contexts from the subbranches of two largest domains of SNOMED CT to perform an FCA-based analysis. Although such a limited sample size may serve to demonstrate feasibility, an exhaustive analysis would be needed to achieve the full potential of the approach.

Most existing algorithms for computing formal concepts are not scalable to very large contexts. The process of generating formal concept hierarchies and constructing concept lattices from large contexts, after formal concepts are identified, is an additional computationally costly step. Due to such challenges, no scalable approaches have been proposed to exhaustively audit the semantic completeness of large biomedical ontologies using FCA, even with the aid of cloud computing technology. To address the computational challenge involved in constructing concept lattices from large contexts, we propose Spark-MCA, a Spark-based Multistage algorithm for Concept Analysis. Spark-MCA implements our proposed new FCA-based algorithms within the Apache Spark distributed cloud computing framework to provide a scalable approach for exhaustively analyzing the semantic completeness of large biomedical ontologies.

Another challenge that impedes the quality assurance of semantic completeness is the lack of reference standards.

Because of the inherent discovery-oriented nature and associated challenges involved in quality assurance work for ontological systems, there is an inevitable lack of “reference standards.” In semantic completeness auditing, case studies are commonly used for validating proof-of-concept. However, for large scale ontological systems, case studies may not be sufficient. We adopt RGT, Retrospective Ground-Truthing,⁵ as a surrogate reference standard for evaluating the performance of auditing methods for semantic completeness. The key idea of RGT is to extract the cumulative concept changes during the evolution of a developing ontology. In this study, for the purpose of evaluating semantic completeness, we focused on the addition and deletion of concepts. We used the cumulative inserted concepts in “delta” files of SNOMED CT between two releases, 201403 and 201609, as the RGT to evaluate the performance of Spark-MCA.

The contributions of this paper are: (1) the introduction of Spark-MCA, scalable distributed algorithms for exhaustively evaluating the semantic completeness within feasible computational times; (2) the application of RGT for validating the performance of FCA-based semantic completeness auditing method. Our results show that Spark-MCA provides a cloud-computing feasible approach for evaluating the semantic completeness of SNOMED CT using formal concept analysis.

1. Background

SNOMED CT Release Cycle. Developed and maintained by SNOMED International, SNOMED CT⁶ is the premier comprehensive clinical terminology for healthcare-related industries worldwide. As required by the meaningful use provisions of the Health Information Technology for Economic and Clinical Health (HITECH) Act,⁷ SNOMED CT is suited for use in clinical documentation in electronic health records (EHR). Clinical data coded in SNOMED CT can be used for multiple purposes.⁸ For example, providers can send SNOMED CT encoded data securely during transitions of care to other providers or upon discharge, or share data with patients themselves. This decreases barriers to the electronic exchange of critical patient information and positively impact patient safety.

SNOMED CT adopted description logic (DL) to formally represent concept meanings and relationships. A normal form of concept expression is a structured combination of subtype relationships (i.e. is-a) and attribute relationships (e.g., associated morphology, causative agent, finding site, part of).⁹ For example, the definition of Shunt of cerebral ventricle to extracranial site is shown in Figure 1 using such a normal form.¹⁰

Figure 1.

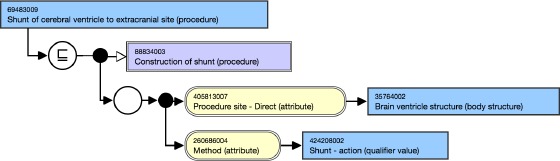
SNOMED CT concept expression for Shunt of cerebral ventricle to extracranial site.

Each SNOMED CT release comes with a “delta” file, which identifies the individual changes that occurred between releases. Table 1 is a fragment of the “delta” file in the SNOMED CT 201609 release. In the “active” column, an entry 1 denotes that a concept (e.g., 128282005) becomes active from this release (i.e., an addition), while 0 denotes that a concept (e.g., 128570000) becomes inactive from this release (i.e., a deletion). We use this file to retrieve cumulative concept changes between releases as RGT to evaluate our Spark-MCA.

Table 1:

A fragment of the delta file in the SNOMED CT 201609 release.

id	effectiveTime	active	moduleId	definition StatusId
128282005	20160731	1	900000000000207008	900000000000073002
128570000	20160731	0	900000000000207008	900000000000074008

Formal Concept Analysis. Formal concept analysis (FCA) has been advocated as a mechanism to audit the quality of SNOMED CT.^4,11-13 FCA is a mathematical method for knowledge engineering. It can be used to derive a concept hierarchy or formal ontology from a collection of objects and their attributes.^14,15 The input data for FCA is a binary relation between a set of objects and a set of attributes. This relation is represented in the form of a formal context, I = (X, Y, R), where X is a set of objects, Y is a set of attributes, and R is a relation R ⊂ X × Y. Each formal context I – (X, Y, R) induces two operators: ↑: 2^X → 2^Y and ↓: 2^Y → 2^X. The operators are defined, for each A ⊂ X and B ⊂ Y:

$$A^{\uparrow }=\left\{y\in Y|\forall x\in A;\left(x,y\right)\in R\right\},B^{\downarrow }=\left\{x\in X|\forall y\in B;\left(x,y\right)\in R\right\}$$

where A^↑ is the set of all attributes shared by all objects in A, and B^↓ is the set of all objects sharing all attributes in B. A formal concept is a pair (A, B) with A ⊂ X and B ⊂ Y such that A^↑ – B and B^↓ – A. The collection of all such pairs, together with the natural partial order (A₁, B₁) < (A₂, B₂) iff A₁ ⊂ A₂ (B₂ ⊂ B₁), form a complete lattice.¹⁴ The structure of the concept lattice corresponds to the hierarchy of formal concepts and provides generalization and specialization between the concepts, i.e., (A₁, B₁) is more specific than (A₂, B₂) (or (A₂, B₂) is more general).

There are two basic algorithmic strategies for computing formal concepts: (a) forming intersections by joining one attribute at a time, and (b) repeatedly forming pairwise intersections starting from the attribute concepts. Kuznetsov and Obiedkov provided a survey and comparative evaluation of algorithms for FCA.¹⁶ Bordat¹⁷ used strategy (a), while Chein¹⁸ used strategy (b). In this study, we use the idea of Troy, Zhang, Tian’s¹⁹ multistage algorithm for constructing concept lattices (MCA) and adapt and extend it in order to take advantage of the scalable distributed Spark framework.

We use ontological definitions for constructing a formal context. One can think of ontological concepts as objects, and ontological relationships as attributes in constructing a formal context. For example, with respect to Figure 1 we can use [69483009|Shunt of cerebral ventricle to extracranial site (procedure)] as an object and the other lines as its attribute entries.

Cloud Computing. Apache Spark is an advanced and high-end upgrade to Hadoop, aimed at enhancing scalability and performance using Resilient Distributed Datasets (RDDs) which facilitates in-memory computations on large clusters in a fault-tolerant manner.²⁰ While both share the key-value conceptual framework, Spark is generally faster than Hadoop for MapReduce because of the way it processes data. It completes the full data analytic operations in-memory and in near real-time: reading data from the cluster, performing the requisite analytic operations, and writing results to the cluster. The in-memory processing strategy makes Spark more suitable for iterative algorithms. However, designing efficient algorithms in a distributed way requires a different strategy than that for the traditional approach, with more attention paid to data locality, job break-down, and trade-offs between parallelism and communication latency.

2. Method

2.1. Overview

In this paper, we introduce Spark-MCA, a distributed algorithm based on MCA, using the theoretical basis of FCA and adapting it to the Spark framework. Spark-MCA contains two parts: distributed MCA for obtaining all concepts, and distributed big set operation for lattice diagram construction. Spark-MCA takes in the original concepts and relations from SNOMED CT in the format described in the previous section as source formal context and generates the entire concept lattice from this context. We illustrate the main steps of our algorithm in the following subsections with the help of an example dataset extracted from SNOMED CT (Table 2).

Table 2:

a: Shunt of cerebral ventricle to extracranial site, b: Neck repair, c: Ventricular shunt to cervical subarachnoid space, d: Creation of ventriculo-jugular shunt, e: Creation of subarachnoid/subdural-jugular shunt. 1: Creation of subarachnoid/subdural-jugular shunt (isa), 2: Brain ventricle structure (Procedure site - Direct), 3: Shunt action (Method), 4: Operation on neck (isa), 5: Surgical repair of head and neck structure (isa), 6: Repair - action (Method), 7: Neck structure (Procedure site - Direct), 8: Creation of connection from ventricle of brain (isa), 9: Repair of spinal meninges (isa), 10: Cervical subarachnoid space (Procedure site - Direct), 11: Spinal cord cerebrospinal fluid pathway operation (isa), 12: Cerebral ventricular shunt to venous system (isa), 13: Structure of jugular vein (Procedure site - Direct), 14: Structure of meningeal space (Procedure site - Direct), 15: Creation of vascular bypass (isa), 16: Anastomosis of veins (isa).

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
a	×	×	×
b				×	×	×	×
c	×	×	×	×	×	×	×	×	×	×	×
d	×	×	×	×	×	×	×					×	×	×
e	×	×	×	×	×	×	×						×		×	×

We performed two types of evaluation: (1) partial validity, and (2) computational performance. To demonstrate that our Spark-MCA can be used in auditing semantic completeness and the results of our algorithm can provide a viable candidate pool of new concepts in a developing ontological system, we apply RGT by comparing the results of Spark-MCA with the concepts added to SNOMED CT versions. For computational performance, we tested our algorithm for its scalability by comparing the running times for datasets of different sizes. We also evaluated our algorithm on its performance on the same dataset but using different numbers of working computer processors.

2.2. Model SNOMED CT Using the FCA

SNOMED CT uses name-value to describe composite expressions. Take

[405813007|Procedure site - Direct (attribute)l 35764002 iBrain ventricle structure (body structure)]

in Figure 1 as an example. Here, 405813007 iProcedure site - Direct (attribute) is the name part, while

35764002| Brain ventricle structure (body structure)

is the value part. We use two steps to construct a formal concept from such SNOMED CT expressions. First, we include SNOMED CT concepts objects and each of their name-value pair as one attribute. For example, Figure 1 is encoded as 69483009: 116680003 → 88834003; 405813007 → 35764002; 260686004 → 424208002, where we used identifiers for simplicity. Second, to enrich the attributes, we include its ancestors’ attributes by leverage transitive closure of the isa relation (identifier 116680003). With the second step, Figure 1 is encoded as 69483009: 116680003 → 138875005; 405813007 → 35764002; 260686004 → 424208002; 260686004 → 129264002, where 138875005 is the root of the sub-hierarchy and dose not have any ancestors.

2.3. Spark-MCA

Algorithm for Distributed MCA

The distributed part of Spark-MCA is built on top of MCA.¹⁹ The idea behind MCA is to perform multistage intersection operations on each pair of concepts from the initial concept set consisting of all objects, until no more new concept is generated. Each of the stages is independent of the previous ones and does not involve any concepts in the previous stages. For notational preparation, define S ⋒ T: – {s ∩ t|s ∈ S, t ∈ T}, where S and T are collections of subsets. With respect to a given formal context (X, Y, R), the MCA algorithm involves the following iterative steps:

$$\begin{array}{ll}{S}_0:=\hfill & \left\{X\right\}\hfill \\ S_1:=\hfill & \left\{{\left\{x\right\}}^{\uparrow }|x\in X\right\},and\hfill \\ S_{i+1}:=\hfill & \left(S_i⋒S_i\right)-{\displaystyle \underset{1\le \kappa \le i}{\cup }{S}_k}\hfill \end{array}$$

for i > 1. One important intermediate step for each stage is to remove all existing concepts ∪_1≤k≤i S_k when forming S_i+1. This way, only newly generated (and necessary) concepts are kept for subsequent stages, resulting in potentially large savings in computational cost.

The strategy involved in designing a distributed algorithm is to decompose a complex job into a sequence of jobs and to distribute particular parts of the data to be processed on different processing nodes. Our idea is to leverage the independence of stages involved in MCA and design a distributed MCA in the following way: Instead of iteratively performing intersections of object concepts pairs, (S_i ⋒ S_i – ∪_1≤k≤i S_k on a single computer in each stage, we employ the MapReduce paradigm to split the iteration of pairwise intersections into a number of partitions. Each partition is then processed on an independent compute node by a Map function. The outputs from the Map functions are then collected, shuffled, and sent to compute nodes to perform Reduce functions. The output of Reduce functions are split again to repeat the above steps. While iterations involved in MapReduce become very expensive in a standard Hadoop MapReduce implementation due to the I/O latency between the MapReduce steps, the distributed MCA implemented using the Spark framework can take advantage of in-memory processing to reduce the I/O latency.

Algorithm 1: Distributed MCA

Data: Formal context (X, Y, R)

Result: Formal concept set C

1 initialize S = {x↑|x ∈ X)

2 candidate = S

3 while |candidate| > 1 do

4 canditade = 0

5 Pair < Int, Int >= S.combination(S)

6 Function Map(p ∈ Pair)

7 | RDD< Int, Int > c = (p.1 ∧ p.2, 1)

8 Function Reduce((c, 1))

9 | candidate = collect(c)

10 C = ∪candidate

11 end

return C

Data in Spark are generally represented in the form of MapReduce key-value pairs <k,v> and stored as resilient distributed datasets (RDDs). Algorithm 1 describes the concept formation phase in Spark-MCA to generate all concepts from a given context. First we initialize the primitive concept set using S = {x^↑|x ∈ X}. Then, each loop in the while block (lines 3-11) performs one pairwise intersection. In each iterative step, we first obtain all pairs of current concepts as the keys for the input to Map (line 5). Then we split the pairs into a number of partitions and send them to compute node. Every node performs Map tasks of intersection on $x_i^{\uparrow }$ and $x_j^{\uparrow }$ (lines 6 and 7). The Reduce tasks collect all keys of Map’s results as candidate concepts to perform next iteration, and add the outcome to the final result (lines 8 - 10). When no new concepts generated, the algorithm stops and returns the set of cumulated formal concepts C.

Table 3 shows the result of new formal concepts generated in each stage. Stage 0 generates all primitive concepts represented by intents. Stage 1 outputs two new concepts: C7 and C8. Stage 2 does not output any new concept, and thus the concepts generation phase stops.

Table 3:

The newly generated formal concepts in each stage for the formal context in Table 2 using Algorithm 1

Stage 0
C1	{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}
C2	{1,2,3}
C3	{4,5,6,7}
C4	{1,2,3,4,5,6,7,8,9,10,11}
C5	{1,2,3,4,5,6,7,12,13,14}
C6	{1,2,3,4,5,6,7,13,15,16}
Stage 1
C7	{1,2,3,4,5,6,7,13}
C8	{1,2,3,4,5,6,7}
Stage 2
C9	{}

Algorithm for Performing Big Set Operations

One criterion for the well-formedness of an ontology is that its hierarchical structure forms a lattice.¹¹ By constructing lattice graphs, we can locate those newly generated concepts in the big picture of the entire ontology and help further inspection of the concept neighbors. With lattice graphs, our result can be a used for other structure-based auditing methods, as well as for visualization.

After all formal concepts are obtained, we have a nature transitively closed relationship with respect to set inclusion. For graph rendering, we need to construct the minimal, irreducible set of subset relations as an irredundant representation of set inclusion (modular transitivity). To do so, we use distributed set operations to construct lattice graphs from the output of the concept concept construction part of MCA (Algorithm 1). We design our lattice construction algorithm by leveraging distributed big set operations using the following strategy adapted from Zhang et al.:^13,21 (1) get all subset relations of one concept, (2) remove other relations except for the minimal supersets. More formally, given a set X in a collection of subsets C, we use ^⇑X to denote the set of all common ancestors of X, i.e., ^⇑X: – {a ∈ C | ∀x ∈ X,x ⊂ a}. Thus, ^⇑X represents the strict upper closure of X. When X is a singleton, i.e., X – {x}, we write ^⇑x for ^⇑{x}. Similarly, we define ^↑X: – {a ∈ C | ∃x ∈ X, x ⊂ a}. We have,^13,21 for any set X, Y ⊂ C,

$${}^{\Uparrow }X={\displaystyle \underset{a\in X}{\cap }{}^{\Uparrow }a},\text{ and }{}^{\uparrow }Y={\displaystyle \underset{b\in Y}{\cup }{}^{\uparrow }b}$$

Hence, the set of minimal upper bounds of X can be obtained using the formula ^⇑X – ^↑(^⇑X).

The distributed big set operations involve two MapReduce jobs: Marking Subset Relations (Algorithm 2) and Transitive Reduction (Algorithm 3). The input of Algorithm 2 is the collection of all formal concepts (intents, say) obtained from Algorithm 1. First we initialize a HashSet C’ to store all concepts and distributed to all computational computers (line 2). Then all concepts are split into partitions to perform MapReduce tasks. In each task, we collect the subsets of concept c_i by iteratively checking each element in C’ to see if it is a subset of c_i (lines 3-12). The output of Marking Subset Relations is a collection of concept-subsets pairs (c_i, a_c), which will serve as the input of Transitivity Reduction. In Algorithm 3, concept and subsets pairs are first cached in CS’ and sent to all nodes (line 2). Then each MapReduce task removes those subsets that are the subsets of the current concept on each pair. This is achieved by removing the union of the subset list S_i for each subset i with concept c in S_c (lines 3-10).

Algorithm 2: Marking Subset Relations

1 Function Marking Subset Relations(C)

Data: Formal concept set C

Result: Concept-subsets pairs S

2 initialize HashSet C’ = Cache(C)

3 Function Map(c ∈ C)

4 a = Φ

5 foreach el ∈ C’ do

6 if el ⊂ c then

7 a ← el

8 end

9 end

10 RDD< Int, Set[Int] > ca = (c, a)

11 Function Reduce(ca(c, a))

12 CS ← (c, a)

13 return CS

Algorithm 3: Transitivity Reduction

Function Transitive Reduction(CS)

Data: Concept-subsets pairs CS

Result: Edge Pairs E

initialize HashSet C’ = Cache(C)

Function Map(cs(c,s) ∈ CS)

S' = Φ

foreach el ∈ s do

s' ← CS'[el] [el]

end

RDD< Int, Set[Int] > pair = (c, s− sO’)

Function Reduce(pair)

E ← (pair)

return E

Table 4 lists all the formal concepts of the formal context given in Table 2. If we equip the associated order on the concepts collection, we obtain the concept lattice shown in Figure 2. In the lattice graph, C₁ contains all the intents and C₉ contains all the extents. Concepts C₁, C₂, C₃, C₄, C₅, in blue, are primitive concepts. Concepts C₇, C₈, in red, are suggested new concepts.

Table 4:

he list of formal concepts generated from the formal context given in Table 2.

Concept	Extent	Intent
C1	{}	{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}
C2	{a}	{1,2,3}
C3	{b}	{4,5,6,7}
C4	{c}	{1,2,3,4,5,6,7,8,9,10,11}
C5	{d}	{1,2,3,4,5,6,7,12,13,14}
C6	{e}	{1,2,3,4,5,6,7,13,15,16}
C7	{d,e}	{1,2,3,4,5,6,7,13}
C8	{c,d,e}	{1,2,3,4,5,6,7}
C9	{a,b,c,d,e}	{}

Figure 2.

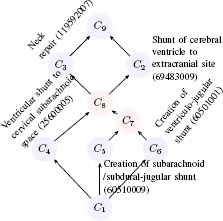
he rendering of concepts in Table 4 as a lattice diagram.

In Spark-MCA, each concept is represented by its intent (and refers neither to the original context, nor to any extent). One can easily incorporate a data structure for looking up the extent of a concept, after all concepts are determined. In this study, we maintain two hash maps: one is C, which, for each concept x e X, collects all its attributes; similarly, the other is A, which, for each attribute y ∈ Y, collects all concepts that contain a particular attribute. Hence, the intersection ${\displaystyle \cap a_i^{\downarrow }}$ where a_i is the attribute of concept c_i, contains all extents of a concept. To identify the labels of formal concepts, we compare their attributes with the primitive concepts list. Concepts corresponding to the primitive concepts are naturally labeled, while the others concepts can be treated as a candidate pool of new concepts for enhancing semantic completeness.

2.4. Evaluation Method

SNOMED CT provides a “delta” file, which contains changes of concepts and relations associated with each release. To evaluate the performance of Spark-MCA, we constructed RGT by obtaining concepts that were added in the releases. Obtaining an appropriate set of changes across multiple SNOMED CT releases is not a mere job of performing unions. For the purpose of evaluation, we constructed a reference set involving two steps: (1) extract added concepts (active value: 1) from all 5 “delta” files from 201403 release to 201609 release; (2) remove deleted or revised concepts (active value: 0) from the added concept sets obtained in the first step. These remaining concepts are selected as a RGT for evaluating the result of Spark-MCA. Since the suggested concepts by Spark-MCA have no labels, we matched the corresponding concepts using their attribute sets (intents).

For scalability analysis, we executed Spark-MCA on Amazon Web Services (AWS) with different hardware configurations. For this study, we selected M4, the latest generation of general purpose instances as the main working configuration. The hardware configuration for M4 is as follows: (1) 2.3 GHz Intel Xeon^® E5-2686 v4 (Broadwell) processors or 2.4 GHz Intel Xeon® E5-2676 v3 (Haswell) processors, (2) EBS-optimized by default.

3. Results

3.1. Semantic Completeness Analysis

We applied Spark-MCA to the SNOMED CT 201403 release and found a total of 500,583 formal concepts suggested by Spark-MCA that were not included in this release. For evaluation, RGT identified 22,687 concepts as additions based on the 5 “delta” files from 201403 to 201609. A total of 3,231 concepts were found in the intersection of the two groups of concepts. This means that Spark-MCA correctly identified 3,231 concepts as missing concepts in the SNOMED CT 201403 release. Table 5 shows the numbers of identified concepts in representative subhierarchies. In this table, “FCA-New” denotes the number of suggested new concepts by Spark-MCA; “Delta” denotes the cumulative number of concept additions based on the “delta” files; “IS-A Only” denotes the number of concepts in “delta” files with no attributes; “New attributes” denotes the number of concepts in the “delta” files whose definition involved attributes that are not in primitive concept list; and “Matched” denotes the number of concepts in the “delta” files that were also found using Spark-MCA.

Table 5:

Comparison of Spark-MCA results and retrospective ground truthing with respect to main subhierarchies.

Subhierarchy (# of concepts)	FCA-New	Delta	IS-A Only	New attributes	Matched
Body structure (30,623)	11,311	743	225	0	353
Clinical finding (100,652)	153,401	10,121	309	5,563	1,825
Pharmaceutical biologic product (16,797)	7,696	2,099	106	1,634	109
Procedure(54,091)	325,114	2,893	178	777	875
Situation with explicit context (3,723)	1,718	991	12	751	45
Specimen (1,475)	1,283	200	10	94	24
Event (3,683)	14	23	23	0	0
Staging and scales (1,308)	6	123	123	0	0

3.2. Scalability Analysis

Scalability is one of the hallmarks of cloud computing. We performed two scalability tests for our Spark-MCA by analyzing computational time for different subhiearchies of SNOMED CT and for different AWS configurations, respectively. For the first test, we selected 4 largest subhierarchies in SNOMED CT 201403 release: Body structure, Clinical finding, Procedure, and Pharmaceutical biologic product. We performed the test on an AWS cluster with 96 processors. The computational time for each subhierarchy is shown in Table 6. For the second test, we repeatedly ran Spark-MCA on the Body structure subhierarchy with different configurations by increasing the number of processors in the AWS cluster. Figure 3 shows the time taken for computing concepts, and Figure 4 shows the time taken for concept lattice graphs. We found a linear decrease of the computational time when the number of computation processors ranged from 1 to 30. When the number of processors approached 100, the computational time tends to cease to decrease, indicating a threshold at which additional processors would not be helpful.

Table 6:

Scalability experiment on different subhierarchies in SNOMED CT.

Subhierarchy	Concepts	Attributes	Time
Pharmaceutical biologic product	16,786	25,107	40 secs
Body Structure	30,623	45,815	3.3 mins
Clinical Finding	100,652	166,123	35 mins
Procedure	54,091	99,995	93 mins

Figure 3.

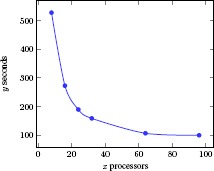
Scalability experiment of distributed MCA.

Figure 4.

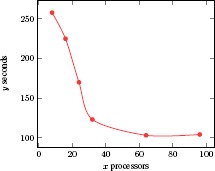
Scalability experiment of lattice construction.

3.3. Evaluation

We applied a Precision-Recall metric to the comparison of our results and RGT. Table 7 shows the P1, R1, and R2 scores in terms of subhierarchies (see the table caption for the definitions of the scores). The P1 values are not so good and we did not calculate the precision by removing concepts in “delta” with no attributes or new attributes. In any case, this would not cause a big difference because of the large number of results from Spark-MCA. For smaller “delta” files, precision may not be so significant. From Table 7 we can see that in the 3 largest hierarchies, Body structure, Clinical finding, and Procedure, our Spark-MCA can identify 47.5%, 18.0%, and 30.2% of all newly added concepts, respectively. If we removed those concepts without attributes or with new attributes, the proportions become even larger. This indicates that Spark-MCA could be a reliable approach for addressing semantic completeness.

Table 7:

P1: ratio of Spark-MCA resulting concepts that can be found in the “delta” files. R1: ratio of delta concepts that can be identified by Spark-MCA, including all concepts from “delta.” R2: ratio of delta concepts that can be identified by Spark-MCA, removing concepts in “delta” with no attributes or new attributes.

Subhierarchy	P1 (%)	R1 (%)	R2 (%)
Body structure	3.12	47.5	68.1
Clinical finding	1.19	18.0	43.0
Pharmaceutical biologic product	1.41	5.2	30.4
Procedure	0.27	30.2	45.1
Situation with explicit context	2.62	4.5	19.7
Specimen	1.87	12	25
Event	0	0	0
Staging and scales	0	0	0

From Table 6, we can see that larger formal contexts required more computational time using our algorithm. However, we point out that because of the density and complexity, we cannot assume that a context with more objects and attributes would necessarily take more computational time. For example, the Clinical finding subhierarchy had more objects (concepts) and attributes, but it needed less computational time than did the Procedure subhierarchy. For Procedure, the process was completed in about 1.5 hours on 96 processors, which might also be completed in days using a sequential approach. From Tables 3 and 4, we can see that as the number of processors increase, the time taken for processing the same dataset declined significantly in the range of 1 to 30 computer processors. Due to the shuffle stage in Spark, the total computational time became stable as the number of processors increase. In conclusion, our computational experiments did demonstrate the scalability of our Spark-MCA algorithm.

4. Discussion

Limitation of Spark-MCA. Although our results showed Spark-MCA to be a practical method in evaluating semantic completeness, there remain a number of limitations. First, Spark-MCA cannot find those added concepts in “delta” involving newly added attributes. For example, Difficulty swimming (714997002) is added with a new attribute 363714003—Interprets (attribute) = 714992008—Ability to swim (observable entity) in the 201603 release, but Spark-MCA did not include it. Other types of lexical or structure auditing methods can be useful supplements to Spark-MCA in auditing semantic completeness. Second, it is less useful to apply the FCA approach to terminological systems with very minimal semantic definitions (e.g., limited to one type of relationship). Subhierarchies in SNOMED CT involving only the isa relation where Spark-MCA suggested no new concepts, even though these were present in the delta files (numbers given in parenthesis indicate additions in the delta files) are: Environment or geographical location (125), Observable entity (418), Organism (1,118), Physical force (0), Physical object (631), Qualifier value (649), Record artifact (32), Model Component (69), Social context (33), Special Concept (0), Substance (2,420).

SNOMED CT versions used for RGT. We used the latest five versions of SNOMED CT (the March 2017 version was released too late to be included in this study) for the feasibility demonstration of our method. This choice was purely a matter of convenience and did not result from methodological or computational limitations of our approach. In fact, it would be desirable to use all the available SNOMED CT versions (in Release Format 1 as well as Release Format 2), with an appropriate starting release as the time-point for computing the formal concepts. All the performance measures would only improve, and the RGT reference set would become larger.

Limitation of RGT. To understand why some concepts suggested by Spark-MCA were not included in SNOMED CT, and some were, we need domain experts assessment and case study to improve gain insights. Such insights may help enhance the method further.

Comparison with related results. We examined the example subhierarchy (hypophysectomy) provided in Jiang and Chute’s work.⁴ We found our results to be in agreement. However, because Jiang and Chute did not provide details about all their findings, we could not perform a more thorough comparison.

Sensitivity of the FCA-based model. FCA-based approach is in general known to be sensitive to the density and complexity of the input formal context. Even though Spark-MCA performed reasonably well for SNOMED CT, we did not perform similar computational experiments on other terminology systems.

5. Conclusion

In this study, we introduced Spark-MCA, a scalable approach for evaluating the semantic completeness of SNOMED CT using an FCA-based method on top of the Spark cloud-computing framework. We formulated SNOMED CT into a formal context in FCA and then used Spark-MCA to exhaustively compute the formal concepts of the context as well as the associated subset relations. We the applied Retrospective Ground-Truthing to assess the performance of Spark-MCA. Our results show that Spark-MCA provides a cloud-computing feasible approach for evaluating the semantic completeness of SNOMED CT using formal concept analysis.