A Note on Parameter Estimate Comparability

Abstract

The use of mixture item response theory modeling is exemplified typically by comparing item profiles across different latent groups. The comparisons of item profiles presuppose that all model parameter estimates across latent classes are on a common scale. This note discusses the conditions and the model constraint issues to establish a common scale across latent classes.

The use of mixture item response theory (IRT) modeling, which is an integration of IRT and latent class models, is exemplified typically by comparing item profiles across different latent groups or latent classes. Mixture IRT modeling provides a useful methodology for identifying latent subgroups of examinees without having to specify group membership in advance and has been applied to a variety of problems, for example, modeling guessing (Mislevy & Verhelst, 1990) or speededness behaviors (Bolt, Cohen, & Wollack, 2002), detection of differences in strategy use in problem solving (Rost & von Davier, 1993), and detection of differential item functioning (DIF; Cohen & Bolt, 2005; Cohen, Gregg, & Deng, 2005; Dai & Mislevy, 2006; Samuelsen, 2008), to name a few. Despite the continued popularity of mixture IRT modeling, there seems to be not enough attention in the mixture IRT literature to the conditions and the model constraints necessary to establish the parameter estimate comparability between different latent classes. This article is a note that discusses the issue of scale comparability between latent classes and what conditions or the model constraints are required to achieve a common scale across latent classes in the mixture IRT modeling.¹ The mixture Rasch model is used (Rost, 1990) for discussion and illustrations.

Scale Comparability Between Latent Classes

Let us assume that the mixture Rasch model is applied for detecting DIF in a set of real item responses from a 20-item test. Also suppose that two distinct latent classes $(g=1\text{and}2)$ exist. A practitioner’s purpose here is to identify unknown latent groups and the different item profiles that characterize the latent classes. The practitioner uses a popular model constraint $\sum {\text{δ}}_{\mathrm{ig}}=0$, where ${\text{δ}}_{\mathrm{ig}}$ is the item difficulty of the ith item in the gth latent class and the summation is over items at a given $g$. Suppose that the model estimation is done and correctly identifies two-class solutions. Now the practitioners have all the results: Two latent classes are identified and 40-item-difficulty-parameter estimates (20 items $\times$ 2 latent classes) are provided. The practitioner starts comparing the item difficulties between the two latent classes and makes conclusions relevant to his or her purpose. No further action regarding the scales of the latent classes is taken by the practitioner. The current mixture IRT literature does not provide any further instructions beyond this in the applications to real data.

Is $\sum {\text{δ}}_{\mathrm{ig}}=0$ sufficient to establish a common scale across the two latent classes for this “real data analysis”? It depends. In the following, the authors posit four scenarios for a test having 20 items and discuss the matter. Note that $\sum {\text{δ}}_{\mathrm{ig}}=0$ is sufficient to establish a common scale within a class, so there is no problem for comparing the model parameter estimates within a class.

First, the truth in the real data is equal to $\sum {\text{δ}}_{\mathrm{ig}}=0$. A common scale is achieved across different latent classes after the estimation of the model with the constraint $\sum {\text{δ}}_{\mathrm{ig}}=0$. No further action is required.

Second, the averages of item difficulties for the two latent classes are the same, but they are not equal to zero, that is, $\sum {\text{δ}}_{\mathrm{ig}=1}=\sum {\text{δ}}_{\mathrm{ig}=2}\ne 0$. A common scale between latent classes is established with the constraint $\sum {\text{δ}}_{\mathrm{ig}}=0$. Again, no further action is required after the model estimation. The origin of the latent scale is arbitrary. What matters is to recover the differences between parameter values which are on a common scale across latent classes. Because the averages of item difficulties are the same for the two latent classes, with the $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint, the item difficulty differences between latent classes are recovered correctly on the same scale regardless of whether the two latent classes follow the same or different ability distributions.

Third, the situation in this scenario is $\sum {\text{δ}}_{\mathrm{ig}=1}\ne \sum {\text{δ}}_{\mathrm{ig}=2}$, with ${\text{θ}}_g~N(\text{μ},{\text{σ}}^2)$. That is, the two latent classes follow the same distribution for ability while there are differences in the item profiles and their averages are not the same. Suppose that the average item difficulty of the second latent class is higher than that of the first latent class by, for example, $\sum {\text{δ}}_{\mathrm{ig}=1}=0$ and $\sum {\text{δ}}_{\mathrm{ig}=2}=20$. There will be systematic bias by the amount of one when the item difficulty estimates of the second latent class are compared with the true item difficulties of the second latent class. Accordingly, the magnitude of the average bias of item difficulty differences between the two latent classes is also one. Does this pose a problem in a simulation study where researchers know the data generating true values such as these? The answer is “no” in the simulation case. The researcher conducting the simulation knows that the mean difference in the latent classes should reflect this average item profile differences. Therefore, the researcher would do adjustment to the estimated item difficulties by using the estimated latent class mean difference. Note here the reasons why the researcher is making a post hoc adjustment for the item difficulties after the model estimation. He or she knows that $\sum {\text{δ}}_{\mathrm{ig}}=0$ is violated in the simulation data and needs to take action on the estimated item difficulties. Also, most of all, note that the key to success in this action of adjustment is that the ability distributions of the latent classes do not have the difference in their means. Otherwise, the latent class mean difference may not correctly show the average item difficulty differences between the two classes. The current mixture IRT literature neither suggest any post hoc linking adjustment to the estimated parameters between latent classes for practitioners’ applications to real data analyses nor make an explicit assumption clearly that latent classes follow the same distribution. In this scenario, it is possible to achieve a common scale across latent classes with the $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint, but it requires a post hoc linking procedure and the assumption of no mean differences in the ability distributions for the latent classes.

Fourth, the latent classes follow different ability distributions in terms of their means $[{\text{θ}}_g~N({\text{μ}}_g,{\text{σ}}_g^2)]$ and item profile differences exist and their averages are not equal to each other $[{\text{θ}}_g~N({\text{μ}}_g,{\text{σ}}_g^2)]$, for example, ${\text{θ}}_{g=1}~N(0,1)$, ${\text{θ}}_{g=2}~N(1,1)$, and the average of item difficulties in the second latent group is higher by 1 than the first latent group, that is, $\sum {\text{δ}}_{\mathrm{ig}=1}=0$ and $\sum {\text{δ}}_{\mathrm{ig}=2}=20$. (Note that the mixture Rasch model is employed here for discussion, where the slope parameters of items in the item response function is unity. Therefore, the difference in ${\text{σ}}_g^2$ does not pose a problem in establishing a common scale between latent classes.) In this case, two latent classes have different means $({\text{μ}}_{g=1}\ne {\text{μ}}_{g=2})$ and the averages of item difficulties from the latent classes are not the same. Estimating the mixture IRT model with the $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint fails to provide a common scale across latent classes. Even the use of the post hoc linking procedure as in the third scenario fails because both the unequal averages of item difficulties and the latent class ability difference exist together. The higher ability of the second latent class $({\text{μ}}_{g=2}=1>{\text{μ}}_{g=1}=0)$ is offset by the same amount of the positive average difficulty difference between the two latent classes $(E({\text{δ}}_{\mathrm{ig}=2})=1>E({\text{δ}}_{\mathrm{ig}=1})=0)$. Thus, the linking adjustment coefficient, estimated by the class mean difference, is zero (or close to zero in using a sample estimate). This is tantamount to no adjustment in the estimated item difficulties for the second latent class. The bias in the item difficulties cannot be corrected even with the post hoc linking procedure using the estimated latent class mean difference. Therefore, the item difficulty differences between the latent classes cannot be recovered correctly.

In real data analyses with the use of $\sum {\text{δ}}_{\mathrm{ig}}=0$, we now have a few choices to ensure the establishment of a common scale across latent classes. First, practitioners simply assume $\sum {\text{δ}}_{\mathrm{ig}}=0$ or $\sum {\text{δ}}_{\mathrm{ig}=1}=\sum {\text{δ}}_{\mathrm{ig}=2}$, which is the least favorable option from the authors’ viewpoint. Second, assume no mean difference in the ability distributions for latent classes and always conduct a post hoc linking procedure using the estimated latent class mean difference. These were never clearly stated in the mixture IRT literature for real data applications. Third, if we do not want to make such an assumption of no mean difference in the ability distributions for the latent classes or $\sum {\text{δ}}_{\mathrm{ig}=1}=\sum {\text{δ}}_{\mathrm{ig}=2}$, we propose the use of class-invariant items, which was also suggested by von Davier and Yamamoto (2004). Those invariant items have the same item difficulties across latent classes. Once a set of class-invariant items are available, estimating the model with both $\sum {\text{δ}}_{\mathrm{ig}=1}=0$ and the equality constraint for the class-invariant items (${\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2}$ [for the two-class solution], where ${\mathbf{\Delta }}_g$ is a vector containing the class-invariant item difficulty parameters for the $g$th class) ensures a common scale across latent classes. The challenge here is to identify class-invariant items. In this regard, some studies exist in the mixture IRT literature (e.g., Cho, Cohen, & Bottge, 2013; Cho, Cohen, Kim, & Bottge, 2010; Finch & Finch, 2013; Leite & Cooper, 2010; Maij-de Meij, Kelderman, & van der Flier, 2008, 2010), where a statistical procedure was applied as an attempt to locate class-invariant items in real data analyses. Finding class-invariant items may be aided by both content-based judgments and statistical procedure. Further studies on how to find class-invariant items in the context of mixture IRT modeling are requested in the future. In spite of this challenge of finding class-invariant items, compared with other constraint approaches discussed previously for establishing a common scale between latent classes, use of class-invariant items is the only approach to recover the parameter differences correctly in both item profiles and ability distributions for latent classes when those differences exist simultaneously.

An alternative, when the estimation method accommodates the latent class population distributions as part of the modeling, is to put constraints on the population ability distributions of latent classes, for example, ${\text{θ}}_g~N(0,{\text{σ}}_g^2)$ for the mixture Rasch model. This constraint ensures parameter estimate comparability within a latent class. Again, similar issues exist in this population distribution mean constraint. The between-class scales may not be always comparable. When ${\text{θ}}_g~N(0,{\text{σ}}_g^2)$ is true in the data or ${\text{θ}}_g~N(\text{μ},{\text{σ}}_g^2)$, where $\text{μ}\ne 0$, that is, the same population mean across latent classes, a common scale is established between latent classes. If this is not the case $({\text{μ}}_{g=1}\ne {\text{μ}}_{g=2})$ and item profiles are different such that averages of item difficulties for latent classes are not the same $(\sum {\text{δ}}_{\mathrm{ig}=1}\ne \sum {\text{δ}}_{\mathrm{ig}=2})$, ${\text{θ}}_g~N(0,{\text{σ}}_g^2)$ is not a sufficient constraint to establish a common scale between latent classes. Thus, we suggest again the use of class-invariant items. In estimating the model, both ${\text{θ}}_{g=1}~N(0,{\text{σ}}_{g=1}^2)$ and the equality constraint ${\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2}$ on the class-invariant items are employed. (The population parameters for $g=2$ and all other parameters are freely estimated without any constraints.)

The discussions made so far are applicable to more general models such as the two-parameter or three-parameter IRT model used in the mixture IRT modeling. ${\text{θ}}_g~N(0,1)$ is not sufficient to provide a common scale between latent classes when the latent class ability distributions are not identical and item profile differences exist with their averages unequal at the same time. With the class-invariant item approach, one may use ${\text{θ}}_{g=1}~N(0,1)$ and the equality constraint ${\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2}$ while all the other model parameters are freely estimated.

Example Analysis

In this section, two example estimation results using a real data and simulation data sets are provided. Note that the purpose of these examples is not to draw substantive conclusions about the data through in-depth analyses, but to demonstrate the impact of different constraints on the comparability of the estimates between latent classes. The first analysis with real data employed dichotomously scored item responses from a 14-item test with the sample size of 109. The test was designed to assess the effects of an instructional intervention for students’ knowledge of mathematics. The second analysis used simulated mixture Rasch model item responses: 21-item dichotomous item responses with the two latent classes $({\text{θ}}_g~N(0,1),\text{where}g=1\text{and}2)$ and item profile differences $(E({\text{δ}}_{\mathrm{ig}=1})=0\text{and}E({\text{δ}}_{\mathrm{ig}=2})=0.6)$. In the simulation, 6 items were simulated to be class invariant, but the sixth item was not constrained to be equal in the class-invariant item constraint approach. The number of simulees was 3,000 for each latent class to ensure high precision of the model parameter estimates.

Two constraint approaches in estimating the mixture Rasch model were used for both real and simulated data. One is $\sum {\text{δ}}_{\mathrm{ig}}=0$ and the other is the class-invariant item approach, where ${\text{θ}}_{g=1}~N(0,{\text{σ}}_g^2)$ and the equality constraint on the class-invariant item difficulties, that is, ${\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2}$. In addition, in the real data analysis, after the model estimation with $\sum {\text{δ}}_{\mathrm{ig}}=0$, a post hoc linking between latent classes was conducted using class-invariant items and its results were compared with the other two constraint approaches.²

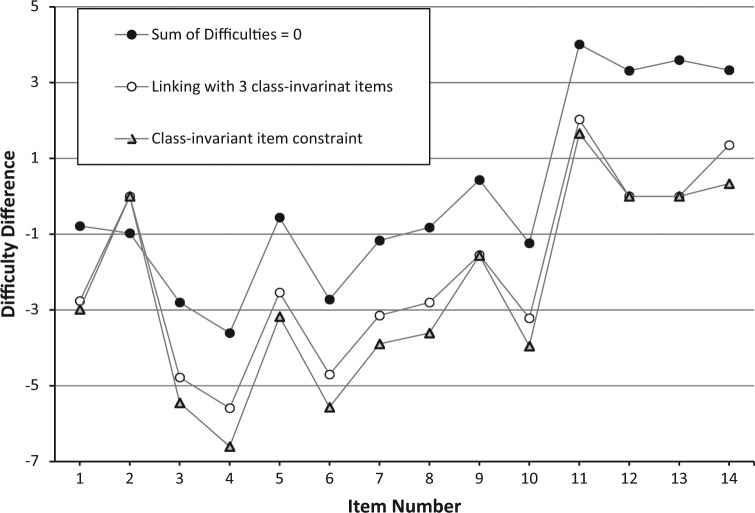
In the first analysis with real data, for the purpose of locating class-invariant items, results from a study (using the same data) by Cho et al. (2010) were used, where they employed both content experts’ knowledge and statistical analysis, and reported three items to be class-invariant. The authors used those three items in the class-invariant item constraint approach in this real data analysis. (Note that using these three items as class-invariant based on a previous study result may not be fully adequate, because there is not yet an unequivocal clear procedure for locating class-invariant items in the literature.) Both constraint approaches identified two latent classes based on Akaike information criterion (AIC) and Bayesian information criterion (BIC) indices. What matters in the estimation of a model, regardless of the chosen constraint approaches, is whether the constraint recovers item difficulty differences correctly (not the item difficulty parameter values themselves). If $\sum {\text{δ}}_{\mathrm{ig}}=0$ is sufficient to establish a common scale between latent classes, item difficulty differences between latent classes should be the same as those from the class-invariant item approach $({\text{θ}}_{g=1}~N(0,{\text{σ}}_g^2)\text{and}{\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2})$. To investigate how close the item difficulty differences between latent classes were in the two constraint approaches, estimates for the item difficulty differences between the two classes are shown in Figure 1. The dark circles indicate item difficulty differences using the $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint and the gray triangles indicate item difficulty differences obtained using the class-invariant item approach $({\text{θ}}_{g=1}~N(0,{\text{σ}}_g^2)\text{and}{\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2})$. Comparison of results in Figure 1 indicates that the two sets of recovered item difficulty differences between latent classes were quite dissimilar.

Figure 1.

Item difficulty differences between two latent classes in a real data analysis.

Furthermore, the post hoc linking (mean-sigma method) between latent classes was conducted using the three class-invariant items. (See Kolen & Brennan, 2004, for IRT scale linking techniques.) The white circles in Figure 1 indicate the results from the linking. The Class 1 estimates were placed onto the Class 2 scale. It is clear that the rescaled item difficulty differences after the linking process are much closer to those of Class 2. Theoretically, the rescaled item difficulty differences after the linking should be the same as those from the class-invariant item approach $({\text{θ}}_{g=1}~N(0,1)\text{and}{\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2})$. Now, we have two clearly distinct sets of estimation results from $\sum {\text{δ}}_{\mathrm{ig}}=0$ and the class-invariant item approach $({\text{θ}}_{g=1}~N(0,1)\text{and}{\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2})$ regarding item profile differences. Which set of item difficulty differences between latent classes would you trust? Without the knowledge of class-invariant items, assuming that the latent class ability distributions have the same mean, a different post hoc linking between latent classes may be conducted using the estimated latent class means as was discussed previously.

The example above used a relatively small data set and results from Cho et al. (2010) to identify the three class-invariant items. Now, we provide another example using simulated data where we know the data generating true item difficulty differences and which items are class-invariant. Biases in the item difficulty difference estimates from the two-class mixture Rasch model application are shown in Table 1 for the $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint and the class-invariant item approach $({\text{θ}}_{g=1}~N(0,1)\text{and}{\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2})$. Items on which their difficulties had equality constraint are indicated by bold type item numbers. The estimation results followed the expected patterns discussed in the previous section.

Table 1.

Bias in Item Difficulty Difference in the Two Constraint Approaches From a Simulation Study.

Item No.	True item difficulty difference	Bias in item difficulty difference
		$\sum {\text{δ}}_{\mathrm{ig}}=0$	$\begin{array}{c}{\text{θ}}_g~N(0,1)\text{and}\hfill \\ ({\mathbf{\Delta }}_{\mathrm{ig}=1}={\mathbf{\Delta }}_{\mathrm{ig}=2})\hfill \end{array}$
	${\text{δ}}_{\mathrm{ig}=1}-{\text{δ}}_{\mathrm{ig}=2}$	${\widehat{\text{δ}}}_{\mathrm{ig}=1}-{\widehat{\text{δ}}}_{\mathrm{ig}=2}$	${\widehat{\text{δ}}}_{\mathrm{ig}=1}-{\widehat{\text{δ}}}_{\mathrm{ig}=2}$
1	−4.0	0.44	−0.15
2	−3.6	0.49	−0.11
3	0.0	0.66	0.00
4	−2.8	0.55	−0.04
5	−3.2	0.60	0.01
6	−2.0	0.69	0.09
7	0.0	0.57	0.00
8	−1.2	0.69	0.10
9	0.6	0.51	−0.09
10	−1.2	0.66	0.07
11	0.0	0.44	0.00
12	−0.8	0.59	−0.01
13	−1.0	0.68	0.08
14	−1.4	0.60	0.00
15	0.0	0.66	0.00
16	2.0	0.59	0.00
17	−0.8	0.64	0.04
18	2.8	0.58	−0.01
19	0.0	0.69	0.00
20	0.0	0.69	0.10
21	4.0	0.55	−0.04
Average	−0.60	0.60	0.00

The $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint alone without any other constraint or the post hoc linking cannot recover the item difficulty differences correctly. Average bias (across all items) for item difficulty difference is 0.6 (see the third column: ${\widehat{\text{δ}}}_{\mathrm{ig}=1}-{\widehat{\text{δ}}}_{\mathrm{ig}=2}$ under $\sum {\text{δ}}_{\mathrm{ig}}=0$ in Table 1), showing the impact of the $\sum {\text{δ}}_{\mathrm{ig}}=0$ constraint. Assuming the distributions of the latent classes have the same means, which is correct in this case, because we simulated the data in such a way, the amount of average bias 0.6 in the item difficulty difference is now properly reflected in the estimated class mean difference. One can use this latent class mean difference to adjust the item difficulties of the second latent group and recover the item difficulty differences correctly. The class-invariant item constraint approach, however, was able to recover the item difficulty differences between latent classes correctly without any follow-up adjustment (see the average bias in the last column in Table 1). If this were the two analyses of a real data set done by two independent researchers (one uses $\sum {\text{δ}}_{\mathrm{ig}}=0$ and the other uses both ${\text{θ}}_{g=1}~N(0,1)$ and ${\mathbf{\Delta }}_{g=1}={\mathbf{\Delta }}_{g=2}$), two sets of clearly dissimilar item difficulty differences (or item profile differences) exist. Note again that for real data analysis, the practitioner using $\sum {\text{δ}}_{\mathrm{ig}}=0$ would simply use the estimation results without being aware of potential scale incomparability between latent classes. The class-invariant item constraint approach achieves a common scale between latent classes without requiring a follow-up adjustment or the assumption of the same mean in the ability distributions for latent classes.

Summary

This article discussed the conditions and the constraint approaches to establish a common scale between latent classes in the application of mixture IRT models. When a multiple-group latent variable modeling is conducted, we always need to deal with the establishment of a common scale across different ability groups whenever they are included in the model. In this regard, the issue of scale linking across latent groups in the mixture IRT modeling is not new at all. Multiple-group IRT (Bock & Zimowski, 1997), test score equating using IRT with a nonequivalent groups anchor test design, and manifest group IRT DIF modeling (e.g., Thissen, Steinberg, & Wainer, 1993), all these need to handle the same issue of a common scale establishment across different groups. One of the key differences between these and the mixture IRT modeling is that the latter does not employ the manifest group membership but latent group membership. The most common solution to set up a common scale across different manifest groups for these applications is to employ a set of common items typically called “anchor items,” whose item parameters are the same across groups. The use of $\sum {\text{δ}}_{\mathrm{ig}}=0$ or ${\text{θ}}_g~N(0,1)$ alone in the mixture IRT modeling is equivalent to a separate calibration for each group in the test score equating or multiple-group IRT applications or manifest group IRT DIF investigations. Without any subsequent linking procedure using the anchor items or a concurrent estimation where the anchor item constraint is utilized, there is no guarantee in establishing a common scale between different groups. (See Kolen & Brennan, 2004, for more details of test score equating design and the equating methods.) If it is appropriate to assume that the two latent or manifest groups follow the same ability distributions (the same ability means in the mixture Rasch case), ${\text{θ}}_g~N(0,{\text{σ}}_g^2)$ (or $\sum {\text{δ}}_{\mathrm{ig}}=0$ with a post hoc linking using the estimated group mean difference) for the Rasch mixture model and ${\text{θ}}_g~N(0,1)$ for the two- and three-parameter IRT mixture models suffice to construct a common scale across different groups. The use of a set of class-invariant items requires identification of such items in advance.³ The issue of finding the class-invariant items is similar to that of finding the anchor (no DIF) items in DIF investigations or linking scales in the presence of DIF. Research regarding refinement or purification of the scale in the DIF literature might provide an initial direction to which mixture IRT modelers may pursue in search of the class-invariant items.

In the mixture IRT literature, despite the surge of its popularity, the issue of scale linking between latent groups did not receive due attention so far. The authors hope that this article facilitates practitioners’ and researchers’ understanding of the scale linking issue across latent classes in the mixture IRT model applications to real data.