Linking Methods for the Zinnes–Griggs Pairwise Preference IRT Model

Abstract

Forced-choice item response theory (IRT) models are being more widely used as a way of reducing response biases in noncognitive research and operational testing contexts. As applications have increased, there has been a growing need for methods to link parameters estimated in different examinee groups as a prelude to measurement equivalence testing. This study compared four linking methods for the Zinnes and Griggs (ZG) pairwise preference ideal point model. A Monte Carlo simulation compared test characteristic curve (TCC) linking, item characteristic curve (ICC) linking, mean/mean (M/M) linking, and mean/sigma (M/S) linking. The results indicated that ICC linking and the simpler M/M and M/S methods performed better than TCC linking, and there were no substantial differences among the top three approaches. In addition, in the absence of possible contamination of the common (anchor) item subset due to differential item functioning, five items should be adequate for estimating the metric transformation coefficients. Our article presents the necessary equations for ZG linking and provides recommendations for practitioners who may be interested in developing and using pairwise preference measures for research and selection purposes.

Over the past few decades, research has shown that noncognitive constructs predict workplace performance and career advancement (e.g., Barrick & Mount, 1991), as well as academic performance, achievement, and retention (e.g., Poropat, 2009). Importantly, noncognitive measures have been shown to provide noteworthy incremental validities for many applications, without the adverse impact that is traditionally associated with cognitive ability tests (Sinha, Oswald, Imus, & Schmitt, 2011).

By far, the most popular approach to gathering noncognitive data is self-report Likert-type measures, where respondents are asked to rate their level of agreement with a series of statements reflecting different levels of noncognitive characteristics. However, measuring these noncognitive characteristics accurately has proven difficult due to response biases such as central tendency, leniency, severity, and halo errors as well as impression management. To deal with these challenges, research dating back to the 1940s has explored forced-choice (FC) formats as alternatives to Likert-type assessments. As noted by Hicks (1970), classical test theory scoring methods traditionally yielded ipsative data, which limited the usefulness of scores.

However, psychometric advances over the last three decades have made it possible to create FC measures that provide the normative scores needed for interindividual comparisons, thus expanding potential applications (e.g., Brown & Maydeu-Olivares, 2013; Stark & Chernyshenko, 2011). Furthermore, recent studies have paid more attention to culture-specific response biases, such as extreme responding and acquiescence, which commonly distort relationships between self-report measures and outcomes of interest in cross-cultural studies (Ferrando, Anguiano-Carrasco, & Chico, 2011). It has also been suggested that FC formats may be effective in reducing these culture-specific response biases (e.g., Ferrando et al., 2011; He, Bartram, Inceoglu, & van de Vijver, 2014). Consequently, researchers and practitioners have begun closely examining the psychometric properties of FC measures and evaluating their predictive utility for research and operational decision making (He et al., 2014).

One of the FC models that has been adopted for some large-scale noncognitive testing applications (e.g., Houston, Borman, Farmer, & Bearden, 2005) is the Zinnes and Griggs (ZG; 1974) ideal point model, which will be described shortly. Recent investigations involving the ZG model have focused on scoring (Oswald, Shaw, & Farmer, 2015) and methods for improving parameter and standard error estimation (Lee, Seybert, Stark, & Chernyshenko, 2014). Recent research has shown that new Markov Chain Monte Carlo (MCMC) estimation methods can recover ZG parameters effectively with samples of 200 to 400 (Lee et al., 2014), which represents a significant improvement over the marginal maximum-likelihood method developed by Stark and Drasgow (2002). The capability to estimate parameters accurately with small samples paves the way for many new applications, but for scores to be compared meaningfully across subpopulations, as in cross-cultural research or multinational selection environments, methods are still needed to link parameters estimated in different examinee groups, as a prelude to measurement invariance testing.

This article addresses that need by developing the equations needed for linking ZG parameters estimated in different examinee groups and comparing the efficacy of test characteristic curve (TCC; Stocking & Lord, 1983) and item characteristic curve (ICC; Haebara, 1980) methods with simpler mean/mean (M/M; Loyd & Hoover, 1980) and mean/sigma (M/S; Marco, 1977) alternatives. (The software developed for this investigation can be obtained from the authors upon request.)

The ZG Ideal Point Item Response Theory (IRT) Model

When an examinee is presented with a pair of statements representing different levels of a noncognitive trait (e.g., conscientiousness or motivation) and is asked to choose the statement that is more descriptive of him or her, the ZG model assumes that the examinee will select the statement that is closer to his or her perceived location on the latent trait continuum. This is expressed formally as follows:

$$P_{\mathrm{st}}\left(\mathrm{\theta }\right)=1-\mathrm{\Phi }\left(a_{\mathrm{st}}\right)-\mathrm{\Phi }\left(b_{\mathrm{st}}\right)+2\mathrm{\Phi }\left(a_{\mathrm{st}}\right)\mathrm{\Phi }\left(b_{\mathrm{st}}\right),$$

where

$$a_{\mathrm{st}}=\frac{2\mathrm{\theta }-{\mathrm{\mu }}_s-{\mathrm{\mu }}_t}{\sqrt{3}},$$

and

$$b_{\mathrm{st}}={\mathrm{\mu }}_s-{\mathrm{\mu }}_t.$$

In Equation 1, $P_{\mathrm{st}}(\mathrm{\theta })$ denotes the probability of selecting statement s over statement t, given the examinee’s trait score (θ) and the respective locations $({\mathrm{\mu }}_s,{\mathrm{\mu }}_t)$ of the statements on the underlying trait continuum. $\mathrm{\Phi }(a_{\mathrm{st}})$ and $\mathrm{\Phi }(b_{\mathrm{st}})$ are cumulative standard normal density functions. Three parameters, $\mathrm{\theta }$, ${\mathrm{\mu }}_s$, and ${\mathrm{\mu }}_t$, are needed to compute response probabilities. As shown by Stark and Drasgow (2002), ZG ICCs are monotonically increasing when ${\mathrm{\mu }}_s$ is greater than ${\mathrm{\mu }}_t$, monotonically decreasing when ${\mathrm{\mu }}_s$ is less than ${\mathrm{\mu }}_t$, and flat when ${\mathrm{\mu }}_s$ equals ${\mathrm{\mu }}_t$. In addition, ZG item information functions (IIFs) peak at the midpoint between the statement locations. Figure 1 presents an illustrative ZG ICC and the corresponding IIF.

Figure 1.

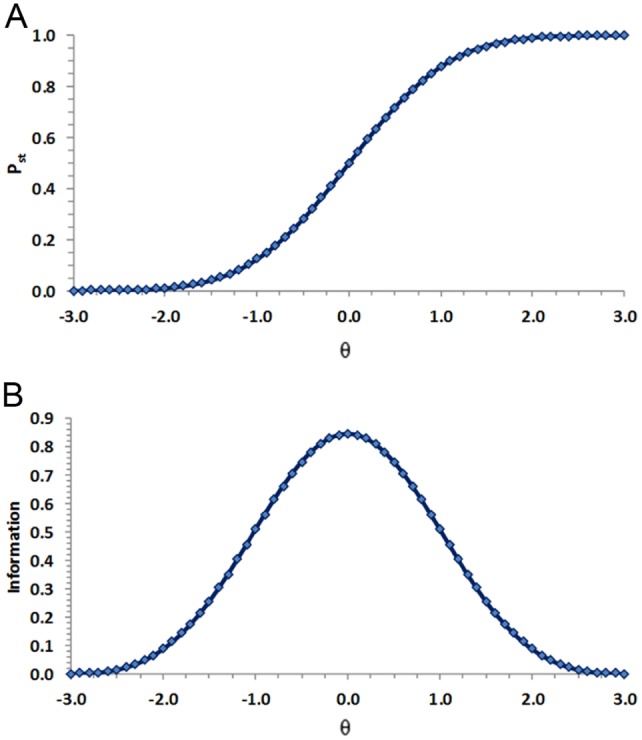
Illustrative ZG item characteristic curve (Panel A) and item information function (Panel B) for an item with stimulus parameters ${\mathrm{\mu }}_s=1.50$ and ${\mathrm{\mu }}_t=-1.50$.

Note. ZG = Zinnes and Griggs.

As discussed by Stark and Drasgow (2002), the slope of a ZG ICC becomes steeper as the distance between the statements composing an item increases. For example, a pair of statements differing in location by 3.0 units would produce a steeper ICC than a pair differing in location by 1.0 unit. Thus, although the ZG IRT model has no explicit discrimination parameter, the slope of the ICCs can still vary. Also, note that ZG item responses are scored 1 if a respondent selects statement s and 0 if a respondent selects statement t.

IRT Linking Methods

Scores based on different test forms or different test settings (e.g., cross-cultural or multinational) must be placed on a common scale to ensure comparable interpretation of scores. This process is referred to as equating or linking (Kolen & Brennan, 2014). Various designs have been proposed to collect data for test linking (Vale, 1986). This study focused on the anchor-item nonequivalent groups design, in which a common subset of items is included in each test form to identify and adjust for differences in the trait distributions of the examinees taking the various forms.

Data collected with an anchor-item nonequivalent groups design can be calibrated concurrently or separately. The latter approach is referred to as separate calibration and linking. In separate calibration and linking, it is common to define one examinee group as a reference group and the other groups as focal groups. Item and person parameters are estimated for each group separately, and a linear transformation is used to put the focal groups’ parameters on the reference group metric. The anchor or common items embedded in the different test forms are used to estimate the coefficients of the linear transformation, A and K, which are known as linking constants or linking coefficients. During item parameter estimation, it is customary to assume a standard normal trait distribution in each group. Differences in the trait distribution across reference and focal groups are therefore reflected in the linking constants, where K indicates the difference in means between a reference group and focal group, and A reflects a difference in the standard deviation or units of measurement.

Letting $\mathrm{\alpha }$, $\mathrm{\beta }$, and $\mathrm{\theta }$ represent item discrimination, location, and person parameter estimates, respectively, letting F represent a focal group, and letting * indicate a transformed parameter, the linear transformation equations can be written generally as follows:

$${\mathrm{\alpha }}_F^{*}={\mathrm{\alpha }}_F/A,{\mathrm{\beta }}_F^{*}=A\times {\mathrm{\beta }}_F+K,\mathrm{and}{\mathrm{\theta }}_F^{*}=A\times {\mathrm{\theta }}_F+K,$$

where ${\mathrm{\alpha }}_F$, ${\mathrm{\beta }}_F$, and ${\mathrm{\theta }}_F$ represent the original focal group parameter estimates, and ${\mathrm{\alpha }}_F^{*}$, ${\mathrm{\beta }}_F^{*}$, and ${\mathrm{\theta }}_F^{*}$ represent the transformed focal group parameter estimates, which can be compared directly with the reference group estimates in, for example, measurement equivalence tests (e.g., Drasgow, 1984).

The goal of IRT linking is to find the coefficients A and K needed for this linear transformation. Several methods have been proposed (e.g., Kolen & Brennan, 2014). These include the moment methods, M/M and M/S, and the characteristic curve methods, TCC and ICC. The M/M method uses the means of the item location and item discrimination parameters to compute A and K, whereas the M/S method uses the means and standard deviations of only the item location parameters. The TCC method finds linking coefficients that minimize the squared difference between the reference and focal group TCCs, whereas the ICC method finds linking coefficients that minimize the sum of squared ICC differences. When different test forms are administered to different groups, the computations involve only the common (anchor) items.

ZG M/M and M/S Linking

Although the ZG model does not explicitly include an item discrimination parameter, item discrimination varies as a function of the difference in the location parameters of the stimuli composing each pairwise preference item. To deal with difference in units of measurement across reference and focal groups, the equations for M/M and M/S linking coefficients were adapted as follows.

If $M(·)$ and $\mathrm{SD}(·)$ represent mean and standard deviation functions, involving a focal group (F) and a reference group (R), then the equations for M/M linking coefficients are as follows:

$$A=\frac{M\left({\hat{\mathrm{\alpha }}}_F\right)}{M\left({\hat{\mathrm{\alpha }}}_R\right)},$$

$$K=M\left({\hat{\mathrm{\beta }}}_R\right)-A\times M\left({\hat{\mathrm{\beta }}}_F\right),$$

where $j=1,2,\dots ,J$ represents the pairwise preference items in the anchor subtest, $\widehat{\alpha }=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$J$}\right.{\displaystyle {\sum }_{j=1}^J|{\widehat{\mu }}_{s_j}-{\widehat{\mu }}_{t_j}|}$ represents the average absolute difference in the respective stimulus location parameters, and $\widehat{\beta }=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$J$}\right.{\displaystyle {\sum }_{j=1}^J({\widehat{\mu }}_{s_j}+{\widehat{\mu }}_{t_j})/2}$ represents the average of the midpoints between the stimuli composing the respective items.

Similarly, the M/S linking coefficients are given by

$$A=\frac{\mathrm{SD}\left({\hat{\mathrm{\beta }}}_R\right)}{\mathrm{SD}\left({\hat{\mathrm{\beta }}}_F\right)},$$

$$K=M\left({\hat{\mathrm{\beta }}}_R\right)-A\times M\left({\hat{\mathrm{\beta }}}_F\right),$$

where $\hat{\mathrm{\beta }}$ is defined above.

ZG TCC Linking

Stocking and Lord (1983) proposed linking reference and focal group metrics by finding the A and K that minimize the squared difference between the TCCs. The loss function F to be minimized is thus

$$F=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left({{\rm T}}_R-{{\rm T}}_F^{*}\right)}^2,$$

where i = 1, 2, 3, . . . , N represents N arbitrary points on the Latent Trait (θ) scale. The true scores in Equation 6 are defined as follows:

$${\mathrm{T}}_R=\sum _{j=1}^{J}P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_R},{\hat{\mathrm{\mu }}}_{t{j}_R}),$$

$$T_F^{*}=\sum _{j=1}^{J}P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_F}^{*},{\hat{\mathrm{\mu }}}_{t{j}_F}^{*}),$$

where ${\hat{\mathrm{\mu }}}_{s{j}_F}^{*}=A\times {\hat{\mathrm{\mu }}}_{s{j}_F}+K\mathrm{and}{\hat{\mathrm{\mu }}}_{t{j}_F}^{*}=A\times {\hat{\mathrm{\mu }}}_{t{j}_F}+K.$

$T_R$ denotes the true score on the set of anchor items from the reference group, and $T_F^{*}$ denotes the true score on the anchor items from the focal group after transformation. J is the number of anchor items.

Note that the true scores in the loss function above may be calculated using latent trait estimates for focal or reference group members. However, evenly spaced nodes of a normal or uniform distribution may be used to avoid unusual weighting of differences due to irregular trait distributions in small samples. In this research, the loss function was calculated using 61 evenly spaced nodes of a uniform distribution, [−3.0, −2.9, . . . , +2.9, +3.0], to equally weight differences across the trait continuum and to insure that the effect of sample size was consistent across methods in the simulation that follows.

To find the linking coefficients that minimize the loss function F, the first partial derivatives with respect to A and K are required. The loss function is minimized when

$$\frac{\partial F}{\partial A}=\frac{-2}{N}\sum _{i=1}^N(T_R-T_F^{*})\frac{\partial T_F^{*}}{\partial A}=0,$$

$$\frac{\partial F}{\partial K}=\frac{-2}{N}\sum _{i=1}^N(T_R-T_F^{*})\frac{\partial T_F^{*}}{\partial K}=0.$$

Using the chain rule of differentiation, the following is obtained:

$$\frac{\partial T_F^{*}}{\partial A}=\sum _{j=1}^J(\frac{\partial P_{\mathrm{ij}}^{*}}{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{sj}}^{*}}_F}\frac{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{sj}}^{*}}_F}{\partial A}+\frac{\partial P_{\mathrm{ij}}^{*}}{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{tj}}^{*}}_F}\frac{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{tj}}^{*}}_F}{\partial A}),$$

$$\frac{\partial T_F^{*}}{\partial K}=\sum _{j=1}^J(\frac{\partial P_{\mathrm{ij}}^{*}}{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{sj}}^{*}}_F}\frac{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{sj}}^{*}}_F}{\partial K}+\frac{\partial P_{\mathrm{ij}}^{*}}{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{tj}}^{*}}_F}\frac{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{tj}}^{*}}_F}{\partial K}).$$

The partial derivatives of the probability function of the ZG model with respect to ${\hat{\mathrm{\mu }}}_{s{j}_F}^{*}$ and ${\widehat{\mu }}_{t{j}_F}^{\ast }$ are as follows:

$$\frac{\partial P_{\mathrm{ij}}^{*}}{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{sj}}^{*}}_F}=\frac{1}{\sqrt{3}}\varnothing \left({\hat{a}}_{\left(\mathrm{st}\right)\mathrm{ij}}^{*}\right)[1-2\mathrm{\Phi }\left({\hat{b}}_{\left(\mathrm{st}\right)j}^{*}\right)]-\varnothing \left({\hat{b}}_{\left(\mathrm{st}\right)j}^{*}\right)[1-2\mathrm{\Phi }\left({\hat{a}}_{\left(\mathrm{st}\right)\mathrm{ij}}^{*}\right)],$$

$$\frac{\partial P_{\mathrm{ij}}^{*}}{\partial {{\hat{\mathrm{\mu }}}_{\mathrm{tj}}^{*}}_F}=\frac{1}{\sqrt{3}}\varnothing \left({\hat{a}}_{\left(\mathrm{st}\right)\mathrm{ij}}^{*}\right)[1-2\mathrm{\Phi }\left({\hat{b}}_{\left(\mathrm{st}\right)j}^{*}\right)]+\varnothing \left({\hat{b}}_{\left(\mathrm{st}\right)j}^{*}\right)[1-2\mathrm{\Phi }\left({\hat{a}}_{\left(\mathrm{st}\right)\mathrm{ij}}^{*}\right)],$$

where $\mathrm{\Phi }(·)$ is the cumulative standard normal function, $\varnothing (·)$ is the standard normal probability density function, ${\hat{a}}_{\left(\mathrm{st}\right)\mathrm{ij}}^{*}=\frac{2{\mathrm{\theta }}_i-{\hat{\mathrm{\mu }}}_{s{j}_F}^{*}-{\hat{\mathrm{\mu }}}_{t{j}_F}^{*}}{\sqrt{3}}$, and ${\hat{b}}_{\left(\mathrm{st}\right)j}^{*}={\hat{\mathrm{\mu }}}_{s{j}_F}^{*}-{\hat{\mathrm{\mu }}}_{t{j}_F}^{*}$.

As ${\hat{\mathrm{\mu }}}_{s{j}_F}^{*}$ and ${\hat{\mathrm{\mu }}}_{t{j}_F}^{*}$ are functions of A, the partial derivatives with respect to A are $\frac{\partial {\hat{\mathrm{\mu }}}_{s{j}_F}^{*}}{\partial A}={\hat{\mathrm{\mu }}}_{\mathrm{sjF}}$ and $\frac{\partial {\hat{\mathrm{\mu }}}_{t{j}_F}^{*}}{\partial A}={\hat{\mathrm{\mu }}}_{\mathrm{tjF}}$.

Substituting these partial derivatives into Equation 12 gives

$$\frac{\partial T_F^{*}}{\partial A}={\displaystyle \sum }_{j=1}^J\left[\frac{1}{\sqrt{3}}\varnothing \left({\widehat{a}}_{\left(st\right)ij}^{*}\right)\left[1-2\Phi \left({\widehat{b}}_{\left(st\right)j}^{*}\right)\right]\left({\widehat{\mu }}_{sjF}+{\widehat{\mu }}_{tjF}\right)-\varnothing \left({\widehat{b}}_{\left(st\right)j}^{*}\right)\left[1-2\Phi \left({\widehat{a}}_{\left(st\right)ij}^{*}\right)\right]{\widehat{b}}_{\left(st\right)j}^{*}\right].$$

Also, as ${\hat{\mathrm{\mu }}}_{s{j}_F}^{*}$ and ${\hat{\mathrm{\mu }}}_{t{j}_F}^{*}$ are functions of K, the partial derivatives of ${\hat{\mathrm{\mu }}}_{s{j}_F}^{*}$ and ${\hat{\mathrm{\mu }}}_{t{j}_F}^{*}$ with respect to K produce $\raisebox{1ex}{$\partial {\widehat{\mu }}_{s{j}_F}^{*}$}\!\left/ \!\raisebox{-1ex}{$\partial K$}\right.=1$ and $\raisebox{1ex}{$\partial {\widehat{\mu }}_{t{j}_F}^{*}$}\!\left/ \!\raisebox{-1ex}{$\partial K$}\right.=1$. Substituting these results into Equation 13 gives

$$\frac{\partial T_F^{*}}{\partial K}=\sum _{j=1}^J\left\{\frac{2}{\sqrt{3}}\varnothing \left({\hat{a}}_{\left(\mathrm{st}\right)\mathrm{ij}}^{*}\right)[1-2\mathrm{\Phi }\left({\hat{b}}_{\left(\mathrm{st}\right)j}^{*}\right)]\right\}.$$

Next, substituting Equations 16 and 17 into 10 and 11, respectively, the linking coefficients, A and K, which minimize the sum of the squared TCC differences can be obtained.

ZG ICC Linking

Haebara (1980) suggested estimating linking coefficients A and K by minimizing the sum of squared ICC differences for a set of anchor items. The quadratic loss function Q to be minimized for the ZG model is

$$Q=\frac{1}{N\times J}\sum _{j=1}^J\sum _{i=1}^N{[P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_R},{\hat{\mathrm{\mu }}}_{t_R})-P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_F}^{*},{\hat{\mathrm{\mu }}}_{t{j}_F}^{*})]}^2,$$

where J represents the number of anchor items and, as above, N represents the 61 nodes of a uniform distribution, [−3.0, −2.9, . . . , +2.9, +3.0].

To estimate the ICC linking constants, the first partial derivatives of Q with respect to A and K are required. This loss function will be minimized when

$$\frac{\partial Q}{\partial A}=\frac{-2}{N\times J}\sum _{j=1}^J\sum _{i=1}^N[P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_R},{\hat{\mathrm{\mu }}}_{t{j}_R})-P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_F}^{*},{\hat{\mathrm{\mu }}}_{t{j}_F}^{*})]\frac{\partial P_{\mathrm{ij}}^{*}}{\partial A}=0,$$

$$\frac{\partial Q}{\partial K}=\frac{-2}{N\times J}\sum _{j=1}^J\sum _{i=1}^N[P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_R},{\hat{\mathrm{\mu }}}_{t{j}_R})-P({\mathrm{\theta }}_i,{\hat{\mathrm{\mu }}}_{s{j}_F}^{*},{\hat{\mathrm{\mu }}}_{t{j}_F}^{*})]\frac{\partial P_{\mathrm{ij}}^{*}}{\partial K}=0.$$

These equations can be used in conjunction with Equations 12 through 17 to solve for A and K.

Method

A C++ program was developed to estimate ZG linking constants (A and K) by four methods, and a Monte Carlo study was conducted to examine effectiveness in conjunction with other factors. The independent variables were as follows: (a) linking method (M/M, M/S, TCC, ICC), (b) sample size per group (50, 100, 200, 400), (c) number of anchor items (5, 10, 20), and (d) linking scenario: focal group trait distribution—N(0,1), N(0.5,1), N(0.5,1.22²). The reference group was designated N(0,1). These distributions were chosen to reflect both impact and dispersion differences across reference and focal groups, as in linking simulations by Koenig and Roberts (2007) and Ogasawara (2001). There were a total of 144 conditions studied $(4\times 4\times 3\times 3)$, and 50 replications were conducted in each condition due to long runtimes for MCMC parameter estimation. More details on the simulation design and execution are provided below.

Horizontal (Equivalent Groups) Versus Vertical (Nonequivalent Groups) Linking

When the latent trait distributions of the reference and focal groups are the same, a linking scenario is referred to as horizontal. When the distributions are different, a linking scenario is referred to as vertical. In our horizontal linking conditions, person parameters for the reference and focal groups were sampled from independent N(0,1) distributions. The expected values of A and K were therefore 1 and 0, respectively. In the vertical linking conditions, person parameters for the reference group were drawn from a N(0,1) distribution, and person parameters for the focal group were sampled from either a N(0.5,1) or a N(0.5,1.22²) distribution. The expected values for vertical linking were thus A = 1, K = 0.5 or A = 1.22, K = 0.5, respectively. In sum, this combination of reference and focal groups resulted in one horizontal linking condition—N(0,1) versus N(0,1)—and two vertical linking conditions—N(0,1) versus N(0.5,1) and N(0,1) versus N(0.5,1.22²).

Number of Anchor Items

For each combination of a reference group and a focal group, three different numbers of anchor items were used to link the metrics: 5, 10, and 20 items. Table 1 displays three common item linking conditions with the anchor items shown in bold print. For the 5-anchor-item condition, Items 16 to 20 were used for both reference and focal groups. For the 10-anchor-item condition, Items 16 to 20 were used. For the 20-anchor-item condition, Items 1 to 20 were used.

Table 1.

Three Different Test Forms With a Set of Anchor Items.

	5-anchor-item condition				10-anchor-item condition				20-anchor-item condition
	Reference		Focal		Reference		Focal		Reference		Focal
Item	${\mathrm{\mu }}_s$	${\mathrm{\mu }}_t$	${\mathrm{\mu }}_s$	${\mathrm{\mu }}_t$	${\mathrm{\mu }}_s$	${\mathrm{\mu }}_t$	${\mathrm{\mu }}_s$	${\mathrm{\mu }}_t$	${\mathrm{\mu }}_s$	${\mathrm{\mu }}_t$	${\mathrm{\mu }}_s$	${\mathrm{\mu }}_t$
1	0.51	3.23	—	—	−0.51	2.03	—	—	−0.51	2.03	−0.51	2.03
2	−2.03	−0.31	—	—	−1.53	1.28	—	—	−1.53	1.28	−1.53	1.28
3	−1.02	0.75	—	—	−1.02	0.75	—	—	−1.02	0.75	−1.02	0.75
4	2.39	−0.50	—	—	2.39	−0.50	—	—	2.39	−0.50	2.39	−0.50
5	−1.79	0.76	—	—	−1.79	0.76	—	—	−1.79	0.76	−1.79	0.76
6	0.75	−1.05	—	—	0.75	−1.05	—	—	0.75	−1.05	0.75	−1.05
7	−0.28	2.09	—	—	−0.28	2.09	—	—	−0.28	2.09	−0.28	2.09
8	1.36	−1.37	—	—	1.36	−1.37	—	—	1.36	−1.37	1.36	−1.37
9	1.13	−0.65	—	—	1.13	−0.65	—	—	1.13	−0.65	1.13	−0.65
10	0.50	2.53	—	—	0.50	2.53	—	—	0.50	2.53	0.50	2.53
11	−2.13	−0.32	—	—	−2.13	−0.32	−2.13	−0.32	−2.13	−0.32	−2.13	−0.32
12	−0.54	0.58	—	—	−1.41	0.58	−1.41	0.58	−1.41	0.58	−1.41	0.58
13	0.29	−2.65	—	—	0.29	−1.64	0.29	−1.64	0.29	−1.64	0.29	−1.64
14	0.35	1.86	—	—	0.35	1.86	0.35	1.86	0.35	1.86	0.35	1.86
15	0.32	−1.87	—	—	0.32	−1.87	0.32	−1.87	0.32	−1.87	0.32	−1.87
16	0.12	2.66	0.12	2.66	0.12	2.66	0.12	2.66	0.12	2.66	0.12	2.66
17	−2.34	0.88	−2.34	0.88	−2.34	0.88	−2.34	0.88	−2.34	0.88	−2.34	0.88
18	1.15	−0.88	1.15	−0.88	1.15	−0.88	1.15	−0.88	1.15	−0.88	1.15	−0.88
19	−0.98	2.12	−0.98	2.12	−0.98	2.12	−0.98	2.12	−0.98	2.12	−0.98	2.12
20	0.50	−1.50	0.50	−1.50	0.50	−1.50	0.50	−1.50	0.50	−1.50	0.50	−1.50
21	—	—	−0.31	1.51	—	—	−1.24	1.26
22	—	—	2.37	0.94	—	—	−0.95	0.52
23	—	—	−1.12	0.82	—	—	1.53	−0.95
24	—	—	1.83	−1.38	—	—	0.85	−2.09
25	—	—	−2.84	0.06	—	—	1.89	−0.32
26	—	—	−1.24	1.26	—	—	−0.63	1.52
27	—	—	−1.95	1.32	—	—	−0.99	2.12
28	—	—	1.53	−0.45	—	—	0.72	2.73
29	—	—	−0.85	−2.09	—	—	−0.84	1.29
30	—	—	1.89	0.12	—	—	−0.44	1.59
31	—	—	−0.63	1.52
32	—	—	0.49	2.82
33	—	—	−1.72	0.32
34	—	—	−1.84	−0.29
35	—	—	−1.84	0.19

Note. Anchor items shown in bold print.

Data Generation

Item response data were generated using a custom C++ program. The generating (true) item parameters, as shown in Table 1, were created in accordance with the recommendations of Stark and Drasgow (2002). Medium and high information items were created by pairing statements that differed by approximately 1.5 and 2.5 units, respectively, to yield information functions that peaked at different parts of the trait continuum. Thus, the test forms were built to mimic conditions that are realistic and desirable in practice. Person parameters were sampled from the previously described trait distributions, response probabilities were computed for each item using the item parameters as shown in Table 1, and responses were scored 1 if the ZG response probability exceeded a random uniform number; otherwise a response was scored 0.

Item Parameter and Linking Coefficient Estimation

An Ox (Doornik, 2009) program was used for MCMC item and person parameter estimation based on Metropolis–Hastings within Gibbs sampling. Fifty thousand total iterations with three chains were performed. After a 20,000 iteration burn-in period, 30,000 iterations were used to compute the final parameter estimates. Estimates of A and K based on the M/M, M/S, TCC, and ICC methods were obtained using a C++ program written by the authors (details for MCMC estimation and linking are available upon request).

Simulation Process

Item parameters were estimated separately for the reference and focal groups, and linking coefficients were computed by the four methods using the common items. The estimated A and K for each method on each replication were used in conjunction with the expected A and K values to compute root mean square errors (RMSEs) and absolute bias statistics for judging overall effectiveness.

Evaluation Criteria and Analytic Method

Bias was examined visually across replications by using scatterplots of the estimated linking coefficients in connection with the expected A and K values. To supplement those results and buttress the interpretation of detailed RMSE and bias findings, ANOVAs were conducted separately on the RMSEs of the estimated A and K values, as in Koenig and Roberts (2007). The nominal Type I error rate for testing each effect was set to .025 (.05/2) to reflect that two dependent variables were studied. Omega squares were also reported to investigate effect sizes, where values of .01, .06, and .14 were used as criteria indicating small, medium, and large effects, respectively (Cohen, 1998).

Results

Table 2 shows the ANOVA results for the main effects and interactions that accounted for at least 1% of the variance in the RMSEs of A and K, considered separately. Linking method had a large effect on the RMSE of A (p < .001, ω² = .505), followed by linking scenario (p < .001, ω² = .218) and sample size (p < .001, ω² = .109). The number of anchor items (p < .001, ω² = .016) had a statistically significant but minimal effect, as did the interaction between linking method and sample size (p < .001, ω² = .041). With regard to the RMSE of K, linking method again had a large effect (p < .001, ω² = .403), which was followed closely by sample size (p < .001, ω² = .388). In contrast to the findings for A, linking scenario had a much smaller effect on the RMSE of K (p < .001, ω² = .070), as did the number of anchor items (p < .001, ω² = .003). As can be seen in the table, some other interactions were significant, but the effects were quite small.

Table 2.

Main and Interaction Effects for Linking Coefficients A and K on RMSEs.

Source	dfB	F	ω2
A
M	3	261.01	.51
LS	2	169.10	.22
S	3	57.32	.11
A	2	13.42	.02
M × S	6	12.84	.04
K
M	3	488.51	.40
S	3	471.27	.39
LS	2	128.08	.07
A	2	6.94	.00
S × LS	6	29.83	.05
M × S	9	10.44	.02
M × LS	6	12.84	.02

Note. All effects shown were significant at p <.025. Only interaction effects that accounted for at least 1% of the variance in power are included. RMSE = root mean square error; df_B = degrees of freedom between; degrees of freedom within = 36 for all effects; ω² = proportion of variance accounted for by the independent variables. M = linking method; LS = linking scenario; S = sample size; A = number of anchor items.

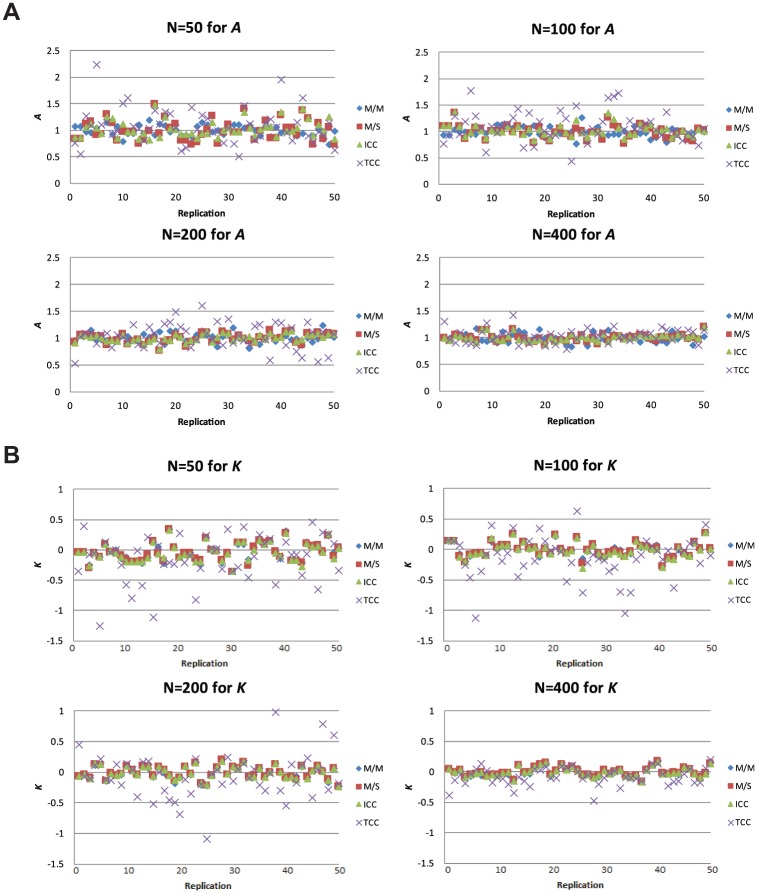
Figures 2A and 2B present scatterplots of the estimated linking coefficients on each replication. Each figure contains four graphs, one for each sample size (N = 50, 100, 200, and 400). The replication numbers are shown on the horizontal axis, and the estimated linking coefficients are displayed on the vertical axis. In these horizontal linking scenarios, the expected values of A and K were 1 and 0, respectively. Generally, the M/M, M/S, and ICC methods produced coefficients that were closer to the expected values than the TCC method. And, as expected, the discrepancy between estimated and expected values decreased as sample size increased. A similar pattern of results was found in other conditions. These plots were not included due to space limitations but can be obtained from the authors upon request.

Figure 2.

Value of estimated A (Figure A) and K (Figure B) coefficients obtained on each replication in the horizontal linking condition with five anchor items.

Note. M/M = mean/mean; M/S = mean/sigma; ICC = item characteristic curve; TCC = test characteristic curve methods.

Table 3 presents the detailed absolute biases and RMSEs of A and K across linking methods, sample sizes, numbers of anchor items, and linking scenarios. The main findings were as follows: First, with regard to linking methods, the M/M, M/S, and ICC methods generally performed well, and they were superior to the TCC method in all conditions. For example, in the horizontal linking scenario with N = 200 and 10 anchor items, the TCC method had RMSE values of .18 and .27 for A and K, respectively. In contrast, the other three methods had RMSE values ranging from .06 to .07 for A and from .12 to .13 for K. The same pattern was observed for the N = 200 vertical linking conditions, N(0.5,1) and N(0.5,1.22²). Together, these results indicate that the M/M, M/S, and ICC methods outperformed the TCC method in connection with the ZG model. However, there were no practical differences among the three because the simpler M/M and M/S methods worked so well.

Table 3.

RMSE and Absolute Bias of Linking Coefficient Across Conditions.

			5 anchor items				10 anchor items				20 anchor items
			n				n				n
Linking coefficients	Linking scenario	Linking method	50	100	200	400	50	100	200	400	50	100	200	400
			RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS	RMSE/BIAS
A	Horizontal	M/M	.10/.01	.09/.01	.09/.01	.08/.00	.10/.00	.06/.00	.06/.00	.05/.01	.07/.01	.06/.01	.05/.00	.05/.01
		M/S	.19/.01	.12/.02	.09/.01	.07/.01	.11/.02	.09/.00	.07/.02	.04/.01	.09/.00	.08/.02	.06/.00	.04/.00
		ICC	.16/.03	.12/.01	.07/.00	.06/.01	.12/.03	.08/.01	.07/.03	.04/.01	.08/.00	.07/.02	.05/.01	.03/.01
		TCC	.34/.08	.30/.09	.24/.04	.13/.04	.29/.08	.21/.03	.18/.05	.15/.02	.32/.14	.29/.09	.20/.09	.19/.09
	Vertical N(0.5,1)	M/M	.10/.01	.10/.05	.10/.00	.08/.02	.10/.03	.06/.01	.06/.00	.06/.01	.06/.02	.05/.00	.05/.02	.05/.00
		M/S	.15/.00	.12/.02	.08/.01	.08/.01	.10/.01	.10/.01	.08/.01	.06/.02	.11/.00	.08/.01	.05/.01	.04/.00
		ICC	.13/.02	.10/.01	.07/.00	.07/.02	.09/.01	.08/.03	.07/.02	.06/.02	.08/.01	.06/.01	.05/.01	.03/.01
		TCC	.33/.01	.27/.01	.24/.03	.13/.02	.29/.06	.25/.09	.20/.02	.18/.06	.26/.07	.24/.07	.21/.06	.18/.07
	Vertical N(0.5,1.222)	M/M	.17/.14	.19/.16	.16/.14	.15/.13	.19/.15	.15/.13	.19/.17	.15/.14	.15/.14	.16/.16	.16/.15	.15/.14
		M/S	.28/.13	.18/.12	.17/.13	.17/.15	.21/.13	.16/.11	.16/.14	.15/.14	.19/.15	.17/.14	.15/.13	.16/.15
		ICC	.26/.15	.18/.12	.17/.14	.17/.15	.19/.14	.17/.14	.16/.14	.16/.15	.21/.19	.18/.17	.17/.16	.17/.16
		TCC	.34/.14	.31/.13	.24/.11	.23/.16	.40/.17	.25/.11	.23/.14	.27/.21	.33/.16	.29/.12	.23/.09	.21/.13
K	Horizontal	M/M	.16/.04	.11/.00	.11/.01	.08/.00	.13/.00	.11/.01	.12/.01	.07/.01	.12/.02	.12/.01	.09/.01	.06/.01
		M/S	.15/.04	.12/.00	.10/.01	.07/.00	.13/.00	.12/.01	.13/.00	.07/.01	.12/.02	.13/.01	.08/.01	.06/.01
		ICC	.16/.04	.13/.01	.10/.01	.07/.00	.13/.00	.12/.01	.12/.00	.07/.01	.12/.02	.12/.01	.09/.01	.06/.01
		TCC	.4/.15	.37/.14	.36/.06	.16/.08	.31/.07	.27/.04	.27/.06	.20/.04	.41/.19	.41/.12	.26/.11	.23/.12
	Vertical N(0.5,1)	M/M	.3/.26	.18/.14	.14/.10	.11/.07	.28/.25	.21/.18	.14/.08	.09/.06	.26/.23	.17/.14	.11/.08	.08/.04
		M/S	.31/.27	.18/.14	.14/.10	.11/.07	.29/.26	.21/.18	.15/.08	.10/.06	.26/.24	.18/.14	.11/.08	.08/.04
		ICC	.3/.27	.19/.15	.14/.10	.11/.07	.30/.27	.21/.17	.14/.07	.09/.05	.26/.24	.18/.15	.12/.08	.08/.05
		TCC	.46/.27	.36/.18	.26/.13	.19/.06	.44/.34	.36/.25	.24/.12	.19/.10	.44/.37	.35/.23	.26/.17	.19/.11
	Vertical N(0.5,1.222)	M/M	.28/.23	.25/.21	.15/.12	.09/.05	.27/.24	.21/.18	.15/.13	.11/.07	.27/.24	.22/.19	.13/.11	.09/.06
		M/S	.29/.24	.25/.20	.15/.11	.09/.06	.27/.23	.22/.17	.14/.11	.11/.06	.27/.25	.22/.19	.13/.10	.09/.06
		ICC	.29/24	.25/.20	.16/.12	.09/.06	.27/.24	.23/.19	.14/.11	.11/.07	.28/.26	.22/.19	.14/.11	.10/.06
		TCC	.44/.33	.37/.20	.26/.12	.16/.06	.40/.27	.30/.21	.21/.12	.15/.02	.41/.26	.41/.26	.28/.11	.17/.06

Note. N(0.5,1) and N(0.5,1.22²) denote person parameters for the target group were sampled from either a N(0.5,1) or a N(0.5,1.22²) distribution. RMSE = root mean square error; M/M = mean/mean; M/S = mean/sigma; ICC = item characteristic curve; TCC = test characteristic curve.

Second, with regard to sample size, it was found that the RMSEs of the linking coefficients decreased as sample size increased. For example, in the N(0.5,1) vertical linking scenario with 10 anchor items, the RMSEs of A and K for the ICC method were .09 and .30 (N = 50), .08 and .21 (N = 100), .07 and .14 (N = 200), and .06 and .09 (N = 400). This improvement with sample size is in accordance with previous research (e.g., Cohen & Kim, 1998; Koenig & Roberts, 2007).

Third, using larger numbers of common items led to small improvements in A and K estimation with the M/M, M/S, and ICC methods in most conditions. For example, for the ICC method with N = 400 under the N(0.5,1) vertical linking scenario, RMSEs and absolute biases of A and K decreased slightly as the number of anchor items increased; RMSEs for A and K were .07 and .11 (|Bias| = .02 and .07) for five anchor items; RMSEs were .06 and .09 (|Bias| = .02 and .05) for 10 anchor items; and RMSEs were .03 and .08 (|Bias| = .01 and .05) for 20 anchor items. However, the results were somewhat inconsistent for the TCC method, which yielded RMSEs for A and K of .13 and .19 (|Bias| = .02 and .06), .18 and .19 (|Bias| = .06 and .10), and .18 and .19 (|Bias| = .07 and .11) for 5, 10, and 20 anchor items, respectively. These results indicate that five anchor items are adequate for linking, even in vertical scenarios, assuming that quality anchor items are chosen.

Finally, recovery of linking coefficients was compared across horizontal and vertical linking conditions. As expected, the biases and RMSEs were smaller under horizontal linking, but the overall results for vertical linking with the M/M, M/S, and ICC methods were still quite good.

Discussion

Our results indicated that the M/M, M/S, and ICC methods outperformed the TCC method under a wide range of conditions. Importantly, the poorer performance of the TCC method cannot be attributed merely to complexity, because the same parameter estimates were used for all linking methods, and the squared differences for both characteristic curve methods were computed using evenly spaced nodes of a uniform distribution, rather than potentially irregular-shaped empirical trait distributions. Moreover, the effectiveness of all methods improved or diminished as a function of sample size. Perhaps the TCC method performed worse because ZG TCCs can be quite flat and sometimes nonmonotonic, depending on the combinations of location parameters in the respective items. This nonmonotonicity may create indeterminacy that affects TCC linking, which is avoided by defining a loss function based on the squared monotonic ICCs. This logic is similar to what was proffered by Seybert, Stark, and Chernyshenko (2013) for the better performance of the ICC method with the generalized graded unfolding model (GGUM; Roberts, Donoghue, & Laughlin, 2000; illustrative TCC plots based on anchor items are provided in our online appendices).

Another finding of this study is that using five anchor items was adequate in both horizontal and vertical linking scenarios; using more anchor items only minimally improved A and K estimation accuracy. However, as discussed in Kolen and Brennan (2014), for example, the choice of anchor items is important and can have a substantial effect on the quality of equating. Ideally, anchor tests should reflect the psychometric properties of the larger instruments in which they are embedded, and potential anchor items should be screened for adequate discrimination and freedom from measurement bias when circumstances permit.

Although our simulation design was based on previously published works that used fixed anchor item sets to reduce the effects of random “noise” (e.g., Cohen & Kim, 1998; Kim & Cohen, 2002), and our generating item parameters were chosen to reflect values encountered in real data (e.g., Stark & Drasgow, 2002), the results needed to be generalized with randomized anchor item sets. Following a reviewer’s suggestion, a brief additional simulation was conducted with random anchor item sets. The horizontal linking scenario and 400 sample size condition for illustration were selected. Following Koenig and Roberts’s (2007) procedure, five and 10 anchor items were randomly selected from the available 20 items. Overall, RMSEs and biases of the linking coefficients were slightly larger with the random anchor item design than with the fixed anchor item design, but the patterns were consistent. In the current study, the test forms consisting of medium and high information items were built to mimic conditions that are realistic and desirable in practice. And, based on this additional simulation, it was believed that the results can be generalized safely to situations involving random anchor item sets of similar size that discriminate adequately (to view the additional simulation results, refer to the online appendices).

Although it was found that linking coefficients were estimated fairly well by M/M, M/S, and ICC methods in some very small sample size conditions, the authors of the present study do not advocate using small samples for ZG parameter estimation. In congruence with statistical theory and previous research on separate calibration and linking (e.g., Hanson & Béguin, 2002; Kim & Cohen, 2002), using larger samples improved results for all methods, and parameter estimation accuracy was not the focus of this study. The authors merely hope that the methods and conditions they explored pave the way for new applications of the ZG model and other types of FC models.