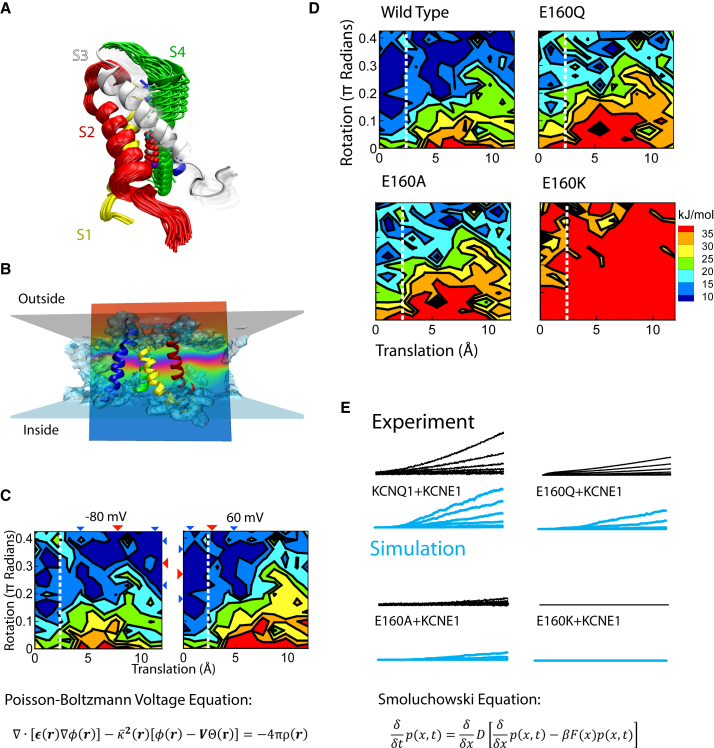
Figure 2.

Probing the molecular underpinnings of VSD transitions and their role in the action potential. Electrostatic calculations were performed on a series of poses to create an energy landscape of VSD activation. This landscape was inserted into an action-potential model to predict ionic currents. By calculating the electrostatic impact on the energy landscape of mutating a negatively charged residue, the consequences for the current and the action potential could be predicted. This figure is modified from (20). (A) As a first pass at simulating VSD activation, several rotations and translations of the S4 helix were investigated. (B) The free energy for each pose was calculated with the Poisson-Boltzmann Voltage equation (21), which is accomplished by inserting the channel model into an implicit solvent. This solvent included a low-dielectric lipid, a transition region, and water. (C) Top: Points on the energy landscape represent a Boltzmann-weighted average of many poses, and after scaling, application of the membrane potential causes the VSDs to transition to the active state at positive potentials and the resting state at negative potentials. Bottom: The Poisson-Boltzmann voltage equation, where φ is the reduced electrostatic potential, r is the position, ϵ is the inhomogeneous dielectric constant, ρ is the density of charge within the protein, $\overline{\kappa }$² represents ionic screening, V is the transmembrane potential, and $\text{Θ}$ is a Heaviside step function. See reference supplement for details (20). (D) Mutating a negative charge on the S2 segment that is positioned to interact with positive charges on the S4 segment caused dramatic changes to the energy landscapes of the VSDs. (E) Top: Using the Smoluchowski equation (18) to allow the four VSDs to travel along these landscapes predicted currents that strongly resembled experimental recordings. Bottom: The Smoluchowski equation, where p(x,t) is the probability of finding a particle at a position x at time t, D is the diffusion constant, F(x) is the force on the particle, and β is 1 over the thermal energy. See reference supplement for details (20).