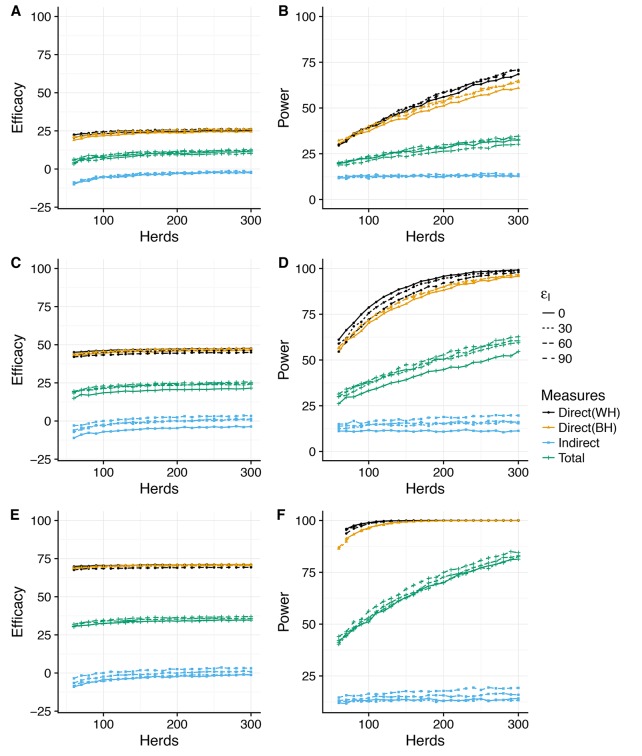
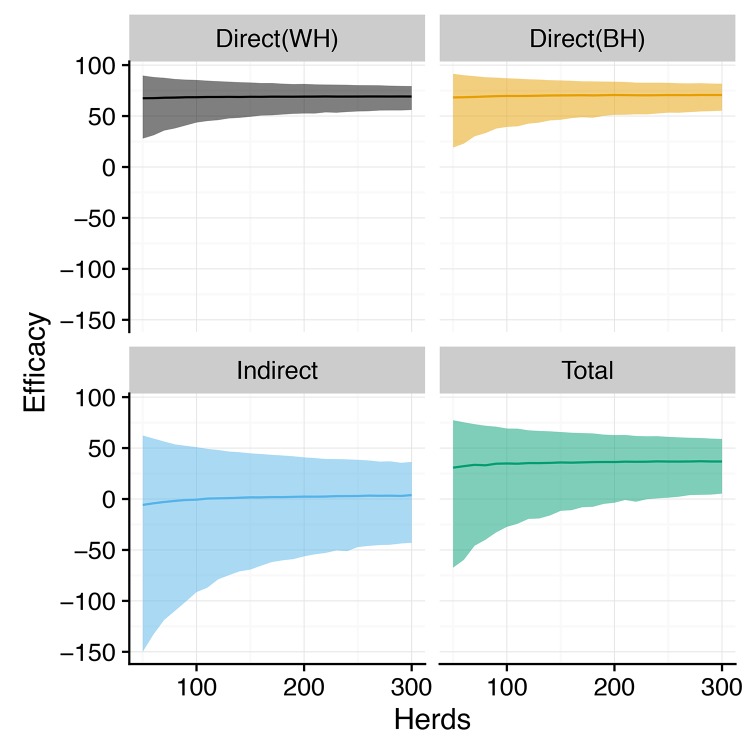
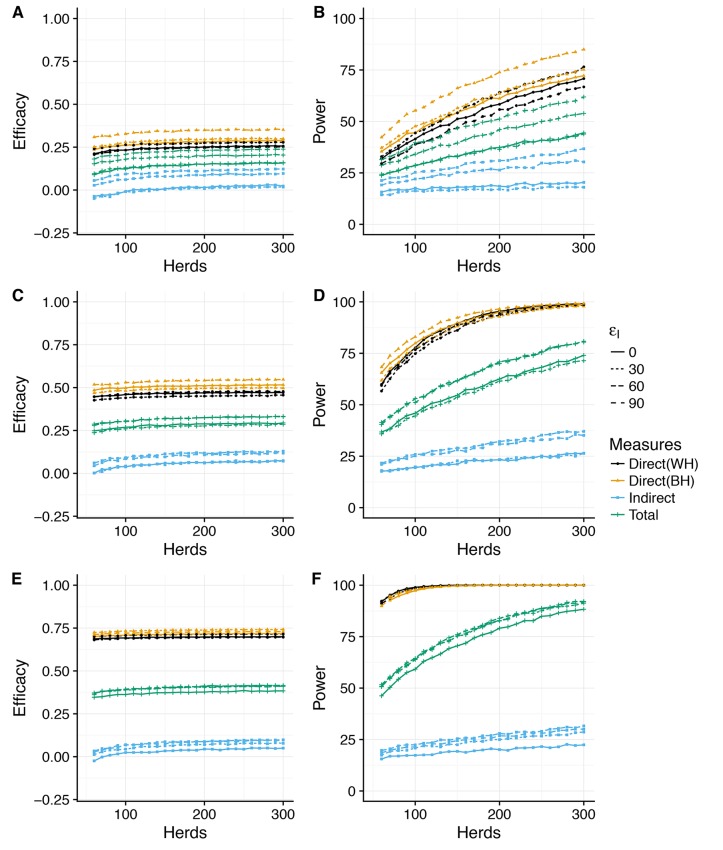
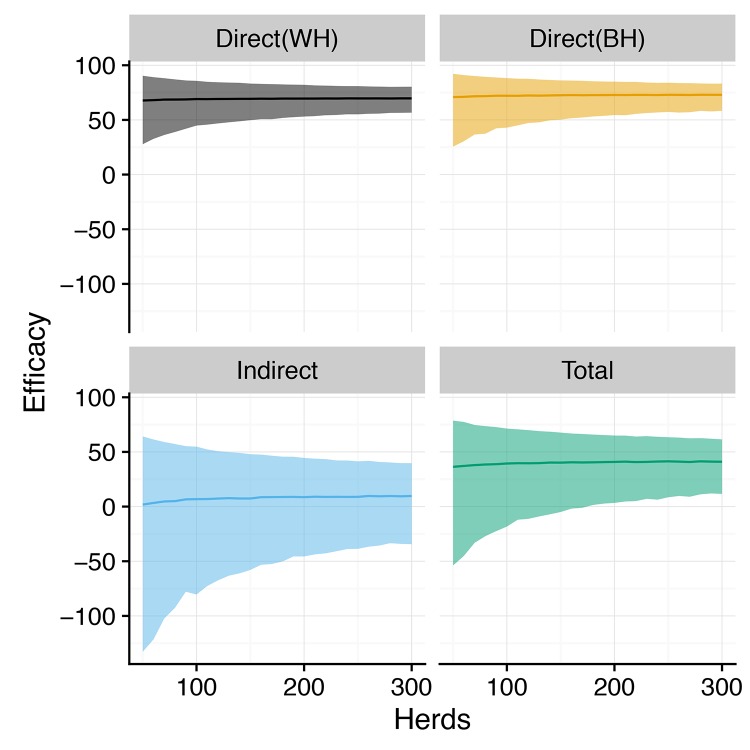
Figure 2. Power to estimate Direct, Indirect and Total efficacy from a two-level design (SORI model).
Expected values of the Direct, Indirect and Total vaccine efficacies measured from a two-level design with trial duration of 3 years and with 75% of herds vaccinated at 50% and 25% of herds as unvaccinated whole-herd controls. We explore a range of assumed vaccine-induced reductions in susceptibility (A,B) , (C,D) , (E,F) ) and infectiousness (Linetype, ). The expected effect sizes (A,C,E) are illustrated by the median of the posterior predictive distribution for each measure. Power (B,D,F) is calculated using a classical hypothesis test on the relative risk of infection (RR) in vaccinated compared to unvaccinated animals (described fully in Materials and methods section). Note that in this design Direct Efficacy can be estimated relative to either within-herd (WH) or between-herd (BH) control animals. 100 herds provides power to estimate a protective direct efficacy for a true efficacy of 60%; however, herds are required to achieve an 80% power to estimate a true efficacy of 30%. The indirect efficacy is predicted to be close to zero as the extrinsic force of infection acting on herds overwhelms the indirect protection provided by immunity within the herd. There is a ~50% probability of estimating a negative indirect efficacy of vaccination across the number of herds explored. As a consequence of the minimal indirect protection offered by vaccination, the Total Efficacy of vaccination with herds with 50% coverage is approximately half that of the direct efficacy. The model predicts that a 90% power of estimating a positive Total Efficacy would require herds for a true direct efficacy of 60%.