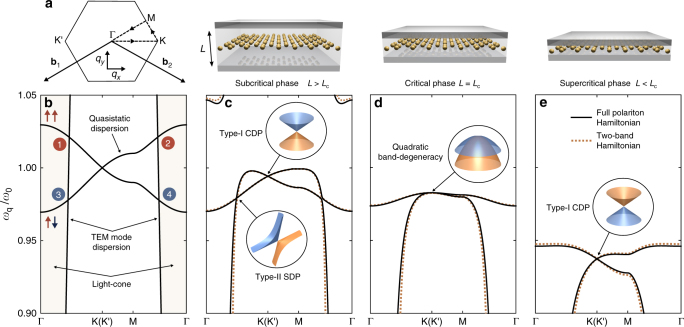
Fig. 2.

Evolution of the polariton dispersion as the cavity height is reduced. a First Brillouin zone defined by primitive reciprocal lattice vectors ${\mathbf{b}}_1=\frac{2\pi }{3a}\left(-\sqrt{3},-1\right)$ and ${\mathbf{b}}_2=\frac{2\pi }{3a}\left(\sqrt{3},-1\right)$. b Quasistatic dispersion of the collective-dipole normal modes, where the upper band corresponds to a bright, symmetric dipole configuration (↑↑) and the lower band corresponds to a dark, antisymmetric dipole configuration (↑↓). The light-cone (shaded region) is bounded by the linear dispersion of the TEM mode. Due to the non-trivial winding in the light–matter interaction (see Fig. 3), the band crossings are expected to result in large (band crossings ‘1’ and ‘2’) or small (band crossings ‘3’ and ‘4’) direction-dependent anticrossings in the polariton spectrum. c–e Polariton dispersion obtained from the polariton Hamiltonian H_pol (solid black lines) and the two-band Hamiltonian ${\overline{H}}_{\mathrm{mat}}$ (orange dashed lines), for c subcritical (L = 5a), d critical (L = L_c = 1.75a), and e supercritical (L = a) cavity heights, respectively. While type-I CDPs with an isotropic Dirac cone (see inset of c) exist even in the quasistatic dispersion (see b), new type-II SDPs with a critically tilted Dirac cone (see inset in c) emerge due to the vanishing light–matter interaction for the dark quasistatic band along the Γ−K(K′) directions (see Fig. 3). At the critical cavity height L_c, three type-II SDPs merge with the type-I CDP (see Fig. 5) resulting in a quadratic band-degeneracy at K(K′) (see inset in d). After criticality, the type-II SDPs annihilate one another and the massless Dirac cone re-emerges at the type-I CDPs (see inset in e) accompanied by an inversion of chirality (see Fig. 5). Plots obtained with parameters ${\omega }_{\mathrm{K}0}^{\mathrm{ph}}=2.5{\omega }_0$ and Ω = 0.01ω₀