Figure 2.

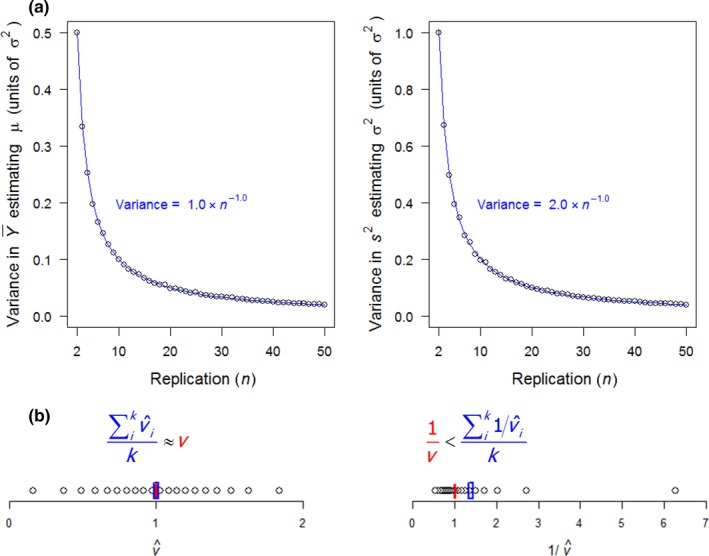
Replication‐dependent variability in estimating the mean and variance. (a) Points show variances in $\overline{Y}$ (left‐hand graph) and in s ² (right‐hand graph) from 10,000 replicate samples of n observations of a normal distribution with mean μ and SD σ. The error in $\overline{Y}$ estimating μ is the ‘error variance’: v = σ²/n (left‐hand graph); the error in s ² estimating σ² is 2v (right‐hand graph). (b) Example of k = 20 observations of ${\widehat{v}}_i$ sampled from a normal distribution around v = 1 (left‐hand graph); inversion imposes right skew, with the distribution of $1/{\widehat{v}}_i$ having mean $(\sum _i^{k}1/{\widehat{v}}_i)/k$ exceeding 1/v, in this case by 39% (right‐hand graph). Consequently, the true meta‐variance, v/k, exceeds the estimated meta‐variance, $1/\sum _i^{k}1/{\widehat{v}}_i$ by the same proportion