Fig. 1.

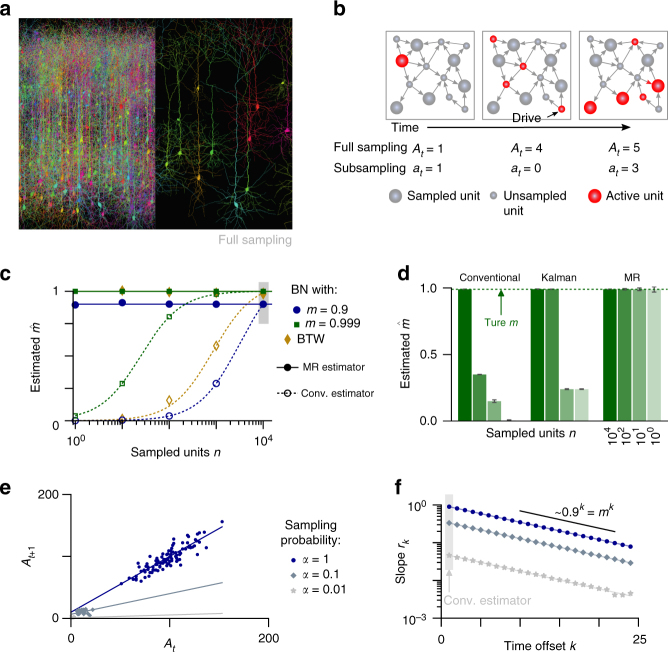
Spatial subsampling. a In complex networks, such as the brain, often only a small subset of all units can be sampled (spatial subsampling); figure created using TREES⁵⁷. b In a branching network (BN), an active unit (e.g., a spiking neuron, infected individual, or defaulting bank) activates some of its neighbors in the next time step. Thereby activity can spread over the system. Units can also be activated by external drive. As the subsampled activity a_t may significantly differ from the actual activity A_t, spatial subsampling can impair inferences about the dynamical properties of the full system. c In recurrent networks (BN, Bak-Tang-Wiesenfeld model (BTW)), the conventional estimator (empty symbols) substantially underestimates the branching ratio m when less units n are sampled, as theoretically predicted (dashed lines). The novel multistep regression (MR) estimator (full symbols) always returns the correct estimate, even when sampling only 10 or 1 out of all N = 10⁴ units. d For a BN with m = 0.99, the conventional estimator infers $\widehat{m}$ = 0.37, $\widehat{m}$ = 0.1, or $\widehat{m}$ = 0.02 when sampling 100, 10, or 1 units, respectively. Kalman filtering based estimation returns approximately correct values under slight subsampling (n = 100), but is biased under strong subsampling. In contrast, MR estimation returns the correct ${\widehat{m}}_{}^{}$ for any subsampling. e MR estimation is exemplified for a subcritical branching process (m = 0.9, h = 10), where active units are observed with probability α. Under subsampling (gray), the regression slopes r₁ are smaller than under full sampling (blue). f While conventional estimation of m relies on the linear regression r₁ and is biased under subsampling, MR estimation infers $\widehat{m}$ from the exponential relation r_k ∝ m^k, which remains invariant under subsampling