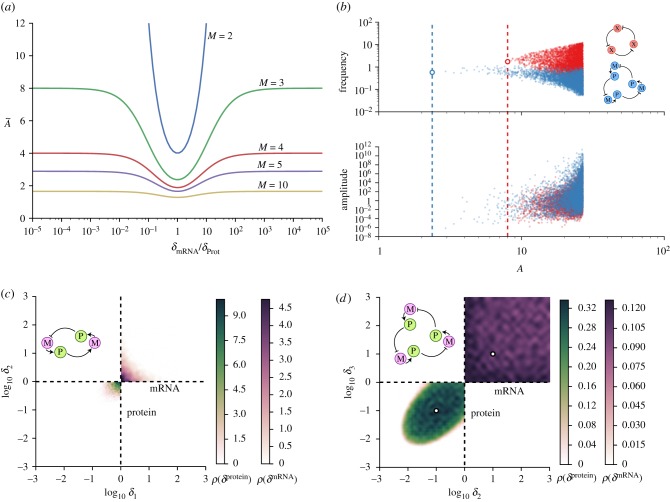
Figure 3.

Effects of mRNA and protein degradation timescale differences. (a) Dependence of critical value of A on the ratio of the degradation rates of the protein and mRNA for a system composed of M genes with protein degradation rate δ_Prot and mRNA degradation rate δ_mRNA. (b) Frequency and amplitude as a function of the network parameter A for 6000 successfully oscillatory networks from a random screening. The random screening was performed for the repressilator network simulated as direct repression between three genes (red) and as a six element network (blue) taking into account separately mRNA from protein dynamics. Dashed lines and rings show the minimum critical value 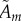and angular velocity at that point α_m predicted by equations (2.13) and (2.14) for N = 3 and N = 6. Repression functions and parameter screening were the same as in figure 2b with additional screening on the degradation rates δ_Prot : [10⁻³, 1] and δ_mRNA : [1, 10³], keeping one of the degradation rates fixed as δ_Prot1 = 1. The translation of mRNA M into protein P is considered to be linear as f_p(m) = a_pm, where a_p was also logarithmically sampled (a_p : [1, 10⁸]). (c,d) Probability density of oscillations for the two (c)) and three (d)) gene network with mRNA (M = 2 and M = 3) for different sets of networks and degradation parameters. The degradation parameters of each test were sampled logarithmically from the ranges δ_mRNA = [1, 10³] (upper quadrant) and δ_Prot = [10⁻³, 1] (lower quadrant). Colours show the successfully oscillatory behaviour probability density of a network as a function of pairs of δ_mRNA and δ_Prot. For the case M = 3, one of the species had fixed degradation rates given by δ_mRNA1 = 10 and δ_Prot1 = 0.1 (white circles). The random sampling of the other parameters of the network was the same as in figure 2b.