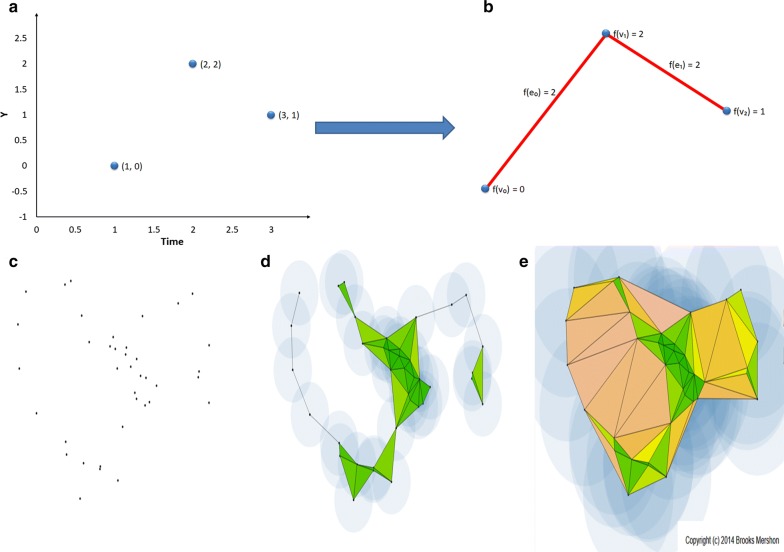
Fig. 2.

Graphical representation of the algorithms for the Piecewise and the Vitetoris-Rips filtrations. a The input signal, formed by three time points with coordinates (1, 0),  (2, 2) and (3, 1) respectively. b The filtered simplicial complex formed by three $0-$simplices: $\{v_0,v_1,v_2\}$ with filter values $f(v_0)=0,f(v_2)=1,f(v_1)=2$ and two $1-$simplices: $\{e_0,e_1\}$, with filter values $f(e_0)=f(e_1)=2$, so the set of filter values is $F=\{0,1,2\}$. c A PCD in a metric space. d Each point is surrounded with a sphere of radius r / 2 such that all the spheres grow up simultaneously and equally. The choice of the parameter r gives rise to certain pairwise intersections of the spheres, which determine the simplices forming the simplicial complex at filtration time r. A pairwise non-empty intersection of dimension k is equal to a $k-1$-simplex. e A sequence of increasing values for the parameter r gives rise to a filtration and a final simplicial complex K is formed with the maximum value of r. The Vietoris–Rips filtration is simply obtained by considering a sequence of increasing values of the parameter r. c, d and e are generated using the software by Brooks Mershon [35]