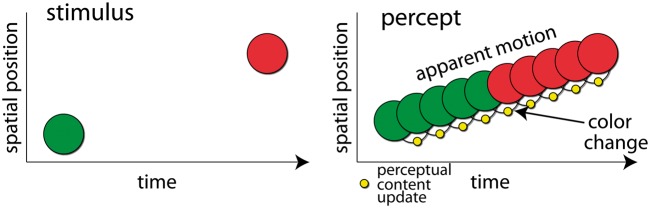
Figure 1.

The color phi illusion. Left: the stimulus sequence during one cycle of the illusion. Right: the corresponding percept. The percept comprises a moving colored circle switching color mid-way. From a discrete perspective this requires that the observer go through k distinct perceptual events: i.e. the circle is at position $x_i$ at time $t_i$ with the color $C_i$ for $i=1,\mathrm{ }2,\dots ,k$. This would entail k + 2 perceptual content updates (blank screen to first circle, circle i to i + 1 and so on). That would mean that while experiencing each cycle of the illusion, the corresponding brain activity must change to bring about the rapidly updating perceptual content, by switching through k + 1 discrete states. Even though switching might be irregular in time, any such k implies a (n approximate) cortical switching rate. In the example shown k = 10. Thus, for a stimulus cycle in this paradigm this would imply at least a rate of 29 Hz of discrete state switching (and see Supplementary Fig. S1). To substantiate prima facie plausibility for a discrete theory, it is necessary to specify plausible upper bounds for k that would square well with our experience (e.g. while watching a movie or a flying bird, listening to music or speech …). Further still, it is necessary to show that cortical networks are indeed capable of implementing this maximal rate of state switching.