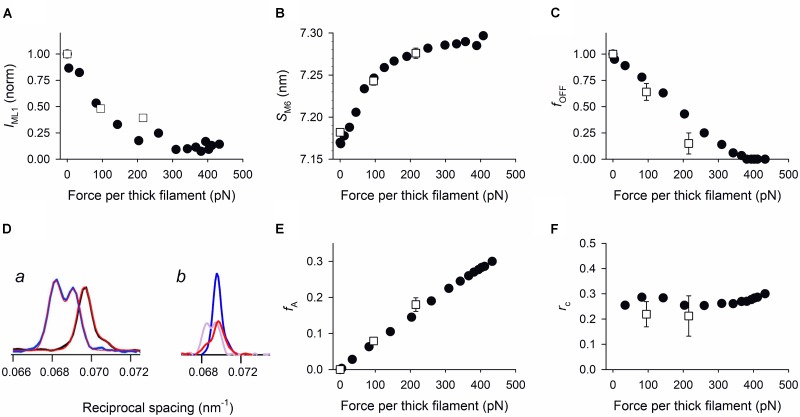
FIGURE 2.
Comparison of force-dependence of the relevant parameters marking the regulatory state of the thick filament. Filled circles: data from force development of isometric tetanus of single muscle fibers; open squares: data from Tp of trabeculae in FE or LC conditions. Force per thick filament in skeletal muscle fiber and heart trabecula is calculated from the force per cross-sectional area reported in the original papers, taking into account the fractional occupancy of the myofibrils, 0.83 in frog skeletal muscle (Mobley and Eisenberg, 1975) and 0.61 in rat trabeculae (Schaper et al., 1985; Barth et al., 1992), and the filament lattice spacing that is the same in both muscles (Irving et al., 2000; Reconditi et al., 2014). The calculated density of thick filaments is 5.87.1014 m-2 and 4.31.1014 m-2 in the skeletal muscle fiber and in the trabecula respectively. (A) IML1, intensity of ML1 reflection. Filled circles from Figure 4B in Reconditi et al., 2011; open squares from Figure S2C in Reconditi et al., 2017. (B) SM6, spacing of M6 reflection. Filled circles from Figure 3d in Linari et al., 2015; open squares from Figure 2F in Reconditi et al., 2017. (C) fOFF, fraction of motors in the OFF state. Filled circles from Figure 3D in Reconditi et al., 2011; open squares from Table 1 in Reconditi et al., 2017. (D) Comparison of the intensity profiles of the M3 reflection in skeletal muscle (a, from Figure 3C in Reconditi et al., 2011; thick black trace, rest; thick blue trace, T0; red lines, outputs of the structural model) and cardiac muscle (b, from Figure 2C in Reconditi et al., 2017; blue trace, diastole; violet and red traces, high force and low force twitch, respectively). The intensity profile of the low force twitch (red trace in b) is solely explained by including the contribution from a substantial fraction of the myosin motors in the OFF conformation. (E) Fraction of actin-attached motors (fA). Filled circles and open squares as in (C). (F) rc, duty ratio. Filled circles calculated from filled circles in (C) and (E). Open squares from Table 1 in Reconditi et al., 2017.