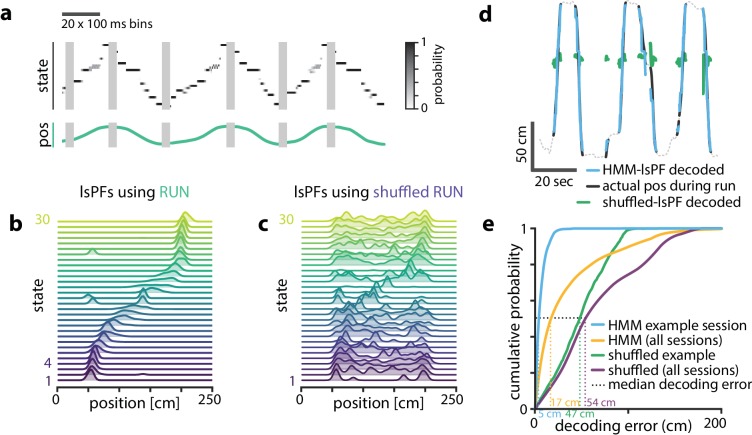
Figure 3. Latent states capture positional code.

Latent states capture positional code. (a) Using the model parameters estimated from PBEs, we decoded latent state probabilities from neural activity during periods when the animal was running. An example shows the trajectory of the decoded latent state probabilities during six runs across the track. (b) Mapping latent state probabilities to associated animal positions yields latent-state place fields (lsPFs) which describe the probability of each state for positions along the track. (c) Shuffling the position associations yields uninformative state mappings. (d) For an example session, position decoding during run periods through the latent space gives significantly better accuracy than decoding using the shuffled tuning curves. The dotted line shows the animal’s position during intervening non run periods. (e) The distribution of position decoding accuracy over all sessions ($n=18$) was significantly greater than chance. ($p<0.001$).

Figure 3—figure supplement 1. Latent states capture positional code over wide range of model parameters.

We investigated to what extent our PBE models encoded information related to the animal’s positional code by learning an additional mapping from the latent-state space to the animal’s position (resulting in a latent-space place field, lsPF), and then using this mapping, we decoded run epochs to position and assessed the decoding accuracy. (a) We computed the median position decoding accuracy (via the latent space) for each session on the linear track ($n=18$ sessions) using cross validation. In particular, we learned a PBE model for each session, and then using cross validation we learned the latent space to animal position mapping on a training set, and recorded the position decoding accuracy on the corresponding test set by first decoding to the state space using the PBE model, and then mapping the state space to the animal position using the lsPF learned on the training set. The position decoding accuracy was significantly greater than chance for each of the 18 sessions ($p<0.001$, Wilcoxon signed-rank test). (b) For an example session, we calculated the median decoding accuracy as we varied the number of states in our PBE model ($n=30$ realizations per number of states considered). Gray curves show the individual realizations, and the black curve shows the mean decoding accuracy as a function of the number of states. The decoding accuracy is informative over a very wide range of number of states, and we chose $m=30$ states for the analysis in the main text. (c) For the same example session, we show the lsPF for different numbers of states. The lsPF are also informative over a wide range of number of states, suggesting that our analyses are largely insensitive to this particular parameter choice (the number of states). The coloration of the lsPF is only for aesthetic reasons.