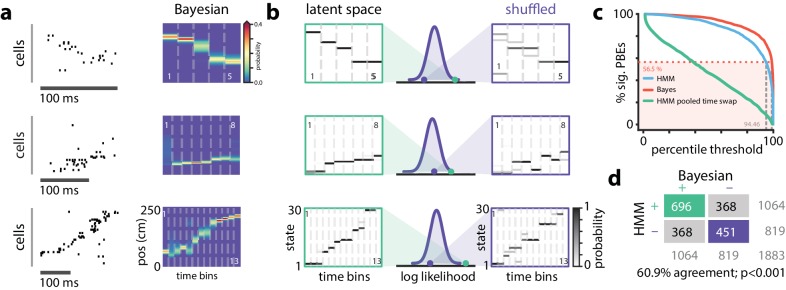
Figure 4. Replay Events Can Be Detected Via HMM Congruence.

(a) Example PBEs decoded to position using Bayesian decoding. (b) (left) Same examples decoded to the latent space using the learned HMM. (right) Examples decoded after shuffling the transition matrix, and (middle) the sequence likelihood using actual and shuffled models. (c) Effect of significance threshold on the fraction of events identified as replay using Bayesian decoding and model congruent events using the HMM approach. (d) Comparing Bayesian and model-congruence approaches for all PBEs recorded, we find statistically significant agreement in event identification (60.9% agreement, $n=1883$ events from 18 sessions, $p<0.001$, Fisher’s exact test two sided).

Figure 4—figure supplement 1. Number of significant PBEs.

(a) The number of Bayesian significant PBEs, as well as the total number of PBEs are shown for each session ($n=18$) when using a significance threshold of 99%. We find that 57% of PBEs (1064 of 1883) are Bayesian significant at this threshold. When using this same threshold for the model-congruence (HMM) significance testing, we find that only 35% of PBEs (651 of 1883) are model congruent. In order to compare the Bayesian and model-congruence approaches more directly, we therefore lowered the model-congruence threshold to 94.46%, at which point both methods had the same number of significant events (1064 of 1883). (b) For each Bayesian significance threshold, we can determine the corresponding model-congruence threshold that would result in the same number of significant PBEs. (c) Using the thresholds from (b) such that at each point, both Bayesian and model-congruence approaches have the same number of significant PBEs, we calculate the event agreement between the two approaches. We note that our chosen threshold of 57% significant events has among the worst agreement between the two approaches.