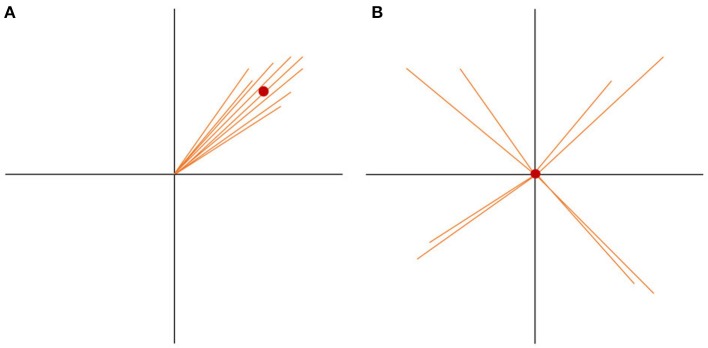
Figure 7.

State-space representation of the randomization statistics used for the TCT. In order to visualize the argument, only two channels (E1, E2) are shown. (A) Shows the distribution of data with high consistency. The vectors represent the individual maps. The red dot is the grand-mean map, which has a relatively large GFP. (B) Shows a random distribution of the data. Note that only the orientation of the individual data, but not the length, has been randomized. Thus, the GFP of each vector stays the same. Notice how the grand-mean map moves to the origin in the case of the random data distribution. It becomes obvious that the GFP of the mean ERP map depends not only on the GFP of the individual maps, but also on the spatial consistency across the individual data. This is the reason the GFP of the mean ERP map of one condition can be chosen as a measure of effect size for consistency.