Bayesian parameter estimation for biochemical reaction networks using region-based adaptive parallel tempering

Abstract

Motivation

Mathematical models have become standard tools for the investigation of cellular processes and the unraveling of signal processing mechanisms. The parameters of these models are usually derived from the available data using optimization and sampling methods. However, the efficiency of these methods is limited by the properties of the mathematical model, e.g. non-identifiabilities, and the resulting posterior distribution. In particular, multi-modal distributions with long valleys or pronounced tails are difficult to optimize and sample. Thus, the developement or improvement of optimization and sampling methods is subject to ongoing research.

Results

We suggest a region-based adaptive parallel tempering algorithm which adapts to the problem-specific posterior distributions, i.e. modes and valleys. The algorithm combines several established algorithms to overcome their individual shortcomings and to improve sampling efficiency. We assessed its properties for established benchmark problems and two ordinary differential equation models of biochemical reaction networks. The proposed algorithm outperformed state-of-the-art methods in terms of calculation efficiency and mixing. Since the algorithm does not rely on a specific problem structure, but adapts to the posterior distribution, it is suitable for a variety of model classes.

Availability and implementation

The code is available both as Supplementary Material and in a Git repository written in MATLAB.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Sampling methods as Markov-chain Monte Carlo (MCMC) are widely used in systems and computational biology to parameterize computational models (Wilkinson, 2007). Applications include biochemical reaction networks (Hug et al., 2013; Xu et al., 2010), spatio-temporal processes (Jagiella et al., 2017) and single-cell data (Zechner et al., 2014). The methods provide samples from the posterior distribution of the parameters given the experimental data and prior knowledge (Andrieu et al., 2003). In contrast to point estimates provided by optimization algorithms, posterior samples facilitate the assessment of parameter and prediction uncertainties (Vanlier et al., 2012) and the tailored design of experiments (Busetto et al., 2009). While uncertainty analysis is beneficial across research fields, in biology these methods are especially important. As experimental data is often sparse and noise corrupted and parameters are often non-identifiable (Chis et al., 2011; Eisenberg and Hayashi, 2014; Fröhlich et al., 2014; Raue et al., 2013), it is essential to unravel these non-identifiabilities and parameter uncertainties to avoid incorrect conclusions and to facilitate reliable predictions.

The evaluation of models used in systems- and computational biology is often computationally demanding, leaving parameter sampling methods on the brink of computational feasibility. To facilitate the often required rigorous statistical assessment of parameter probability distributions in those applications, efficient sampling algorithms are inevitable. One natural way to maximize the efficiency of sampling algorithms is to reduce the auto-correlation of the generated chains (Andrieu et al., 2003). A high auto-correlation implies that consecutive points in the Markov-chain are correlated. Accordingly, the model has to be evaluated multiple times to generate a single independent sample of the posterior, lowering the effective sample size (ESS; Girolami and Calderhead, 2011). Decreasing the auto-correlation lowers the necessary chain length required for a representative posterior sample.

The auto-correlation achieved using an MCMC algorithm can be reduced by employing a tailored proposal density. In the literature, three concepts for the tailoring of the proposal density are proposed, which are independent of the underlying model: (i) Adaptive Metropolis (AM) samplers improve the global proposal density based on the already available chain [(Andrieu and Thoms, 2008; Haario et al., 2001; Roberts and Rosenthal, 2009)]. (ii) Hamiltonian Monte–Carlo, Riemannian Monte–Carlo and related sampling approaches exploit the local geometry of the posterior, such as 1st and 2nd order derivatives, to construct an appropriate local proposal density [(Girolami and Calderhead, 2011; Graham and Storkey, 2017; Hoffman and Gelman, 2014; Lan et al., 2014)]. (iii) Region-based methods split the parameter domain in different regions and assign appropriate proposal densities for each of the individual regions [(Bai et al., 2011; Craiu et al., 2009)]. Some of these methods have also been combined, e.g. region-based adaptive Metropolis (RB-AM) samplers (Bai et al., 2011).

Complementary, small-world sampling [(Guan and Krone, 2007; Yang et al., 2016)] and delayed rejection AM (Haario et al., 2006) has been introduced. These methods employ multi-component and multi-try proposals, respectively, and can be combined with the aforementioned approaches. All of these different concepts boosted the sampling performance of MCMC methods, but the auto-correlation for posteriors with multiple modes usually remains high (Ballnus et al., 2017). To address this, multi-chain algorithms such as Parallel Tempering (PT; Łącki and Miasojedow, 2016; Miasojedow et al., 2013; Sambridge, 2013; Vousden et al., 2016) and Parallel Hierarchical Sampling (Hug et al., 2013; Rigat and Mira, 2012) have been introduced. These algorithms aim to improve mixing by increasing the frequency of jumps between modes and the exploration of tails. Interestingly, studies have shown that for multi-chain methods the local exploration becomes problematic and limits the mixing (Ballnus et al., 2017).

In this manuscript, we propose a sampling algorithm which addresses differences between local- and global posterior properties to improve the mixing and to decrease the autocorrelation. The algorithm combines PT with region-based adaptation. This allows efficient transitions between modes and a good local exploration at the same time. To facilitate the application of the algorithm, all steps are automatized, including the construction of the regions and the adaptation of the proposal density. We systematically assessed and evaluated the proposed algorithm using established benchmarks as well as application problems, and compared it to state-of-the-art RB-AM and PT methods. We show that the presented method has the potential to improve sampling efficiency and robustness for posterior distributions with multiple modes or pronounced tails––properties often found in biological problems with non-identifiabilites (Chis et al., 2011; Eisenberg and Hayashi, 2014; Fröhlich et al., 2014; Raue et al., 2013)––substantially.

2 Materials and methods

In this section, we propose the Region-based Adaptive PARallel Tempering method (RAmPART). We outline RAmPARTs properties and provide insights into the implementation. Additionally, we briefly introduce the pipeline, which was applied for the evaluation of the different methods.

2.1 Problem statement

We consider the problem of sampling the posterior distribution $\pi (\theta |\mathcal{D})$ of the parameter $\theta \in \Omega \subset {ℝ}^n$ given the data $\mathcal{D}$. Following Bayes’ Theorem, the posterior distribution is

$$\pi (\theta |\mathcal{D})=\frac{\pi \left(\mathcal{D}\right|\theta )\pi (\theta )}{\pi \left(\mathcal{D}\right)}$$ (1)

in which $\pi \left(\mathcal{D}\right|\theta ),\hspace{0.17em}\pi (\theta )$ and $\pi \left(\mathcal{D}\right)$ denote likelihood, prior and marginal distribution. Depending of the model and dataset, posterior distributions can possess different properties, including multiple modes, pronounced tails and differences between local and global structure. These properties are usually unknown prior to the sampling, hence, we consider the problem of developing a robust multi-purpose method.

2.2 RAmPART algorithm

In this study, we propose a sampling algorithm which combines RB-AM and PT.

RB-AM algorithms construct a Markov-chain for the parameters $\theta \in \Omega$ with target distribution $\pi \left(\mathcal{D}\right|\theta )$. To account for the potentially complex geometry of the posterior distribution, the parameter domain Ω is split into regions Ω_r, $r=1,\dots ,R$ (Craiu et al., 2009). Each region Ω_r possesses an individual proposal density $q_r^{\left[i\right]}(\theta \prime |{\theta }^{\left[i\right]})$, in which i is the index of the iteration. The union of all regions corresponds to Ω. The regions and region-specific proposal densities are constructed adaptively for instance using Gaussian Mixture Models (GMMs). In comparison to classic AM algorithms which use a single, global proposal density, RB-AM adds a high degree of freedom to the way new sample points are proposed across different parts of the posterior.

PT algorithms construct a Markov-chain on a product space ${\Omega }^L:=\{\mathit{\theta }=({\theta }_1,\dots ,{\theta }_L\left)\right|{\theta }_{\ell }\in \Omega ,\ell =1,\dots ,\mathit{L}\}$ where L is the number of temperature levels (Łącki and Miasojedow, 2016; Vousden et al., 2016). The target distribution on the product space is defined as the product of tempered posterior distributions,

$$\pi (\mathit{\theta }|\mathcal{D})\propto \prod _{\ell =1}^L{\pi }^{1/{\tau }_{\ell }}({\theta }_{\ell }\left|\mathcal{D}\right),$$ (2)

with temperatures ${\tau }_{\ell },\hspace{0.17em}\ell =1,\dots ,L$, such that $1={\tau }_1<{\tau }_2<\dots <{\tau }_L$. The sequence of points ${\theta }_{\ell }^{\left[i\right]}$ for a temperature $\ell$, is referred to as the $\ell$th chain. The Markov-chain on the product space performs random walk steps for each chain and random swaps between chains. As chains with high temperatures travel more easily between different regions, e.g. different modes and tails, chains generated using PT often possess a lower auto-correlation than single-chain algorithms (Ballnus et al., 2017).

RB-AM and PT are applicable to a wide range of problems, yet, the sampling performance is often unsatisfactory. We illustrate in the Results Section, that RB-AM has difficulties to travel between different parameter regions with high probability mass and PT suffers from differences between local and global correlation structure. To address these shortcomings, we propose the Region-based Adaptive PARallel Tempering (RAmPART algorithm). RAmPART constructs a Markov-chain on a product space ${\Omega }^L$ by interweaving random walk steps and random swaps, as in PT. For each of the tempered sub-chains, a region-based proposal density, constructed and adapted over time as in RB-AM algorithms, is employed. In the following, we describe the mathematical and implementation details.

The proposed method has two phases: warm-up and sampling phase. In the warm-up phase, parameter regions Ω_r, $r=1,\dots ,R$, are constructed which are suited for efficient sampling with Gaussian proposal densities. In principle, different approaches could be employed to determine such regions, including the use of information obtained in a preceding multi-start local optimization. RAmPART runs an PT algorithm (Ballnus et al., 2017; Łącki and Miasojedow, 2016; Vousden et al., 2016), which uses an adaptive Gaussian proposal for the random walk steps (Fig. 1a), an adjacent proposal for random swaps and temperature adaptation following (Vousden et al., 2016). A short run of this PT algorithm yields a sample which is supposed to capture the high-probability regions of the posterior. This sample is usually not representative for the posterior distribution, but is sufficient for the warm-up phase. Using the sample, a GMM is trained with an expectation-maximization (EM) algorithm (Murphy, 2012; Fig. 1b), yielding

$$\text{GMM}(\theta )=\sum _{r=1}^R{w}_r\mathcal{N}(\theta |m_r,C_r),$$ (3)

with weights ω_r, means m_r and covariance matrices C_r, $r=1,\dots ,R$. The appropriate number of mixture components is determined using 5-fold cross-validation with the BIC as selection criterion. As the GMM approximates the posterior distribution, we assume that in the parameter region

$$\begin{array}{l}{\Omega }_r=\{\theta \in \Omega |\forall r\prime \in \{1,\dots ,R\}\backslash \hspace{0.17em}r,\\ w_r\mathcal{N}(\theta |m_r,C_r)\ge w_{r\prime }\mathcal{N}(\theta |m_{r\prime },C_{r\prime })\},\end{array}$$ (4)

in which the rth mixture component dominates, a Gaussian proposal density with covariance matrix C_r can achieve a good sampling performance. Accordingly, in the following, the parameter regions Ω_r, $r=1,\dots ,R$, are used in random walk steps (for all temperatures).

Fig. 1.

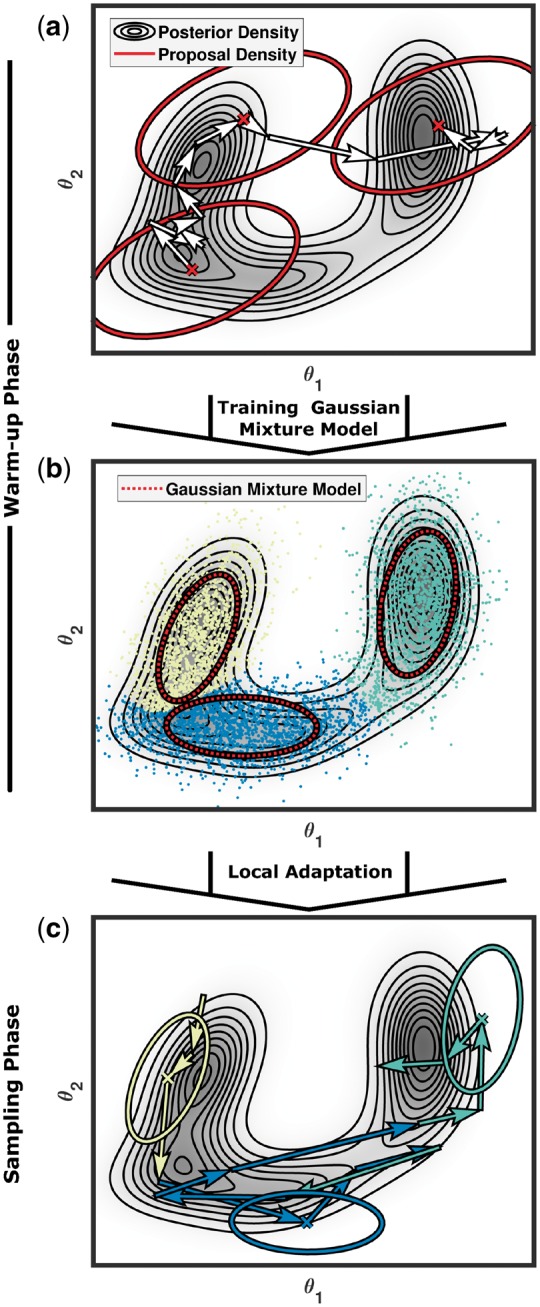
Visualization of the 2-phase sampling process employed by RAmPART. (a) In the warm-up phase, the posterior distribution is sampled with a PT algorithm which adapts to the global covariance structure. (b) The posterior samples (which might not be representative) are used to define regions in the posterior which can be approximated using a GMM. The GMM defines three regions and each of the sample points is associated with one them represented by the yellow, green or blue colour. (c) In the sampling phase, the regions are used to adapt region-specific proposal densities. The adaptation of the covariance matrices in the warm-up and sampling phase is performed for each temperature separately

Remark: Information about the posterior distribution can be exploited to provide user-defined regions Ω_r or to restrict the GMMs to a subset of the parameters. This potentially improves robustness and computational efficiency, or allows to skip the warm-up phase completely.

In the sampling phase the afore-derived parameter regions Ω_r, $r=1,\dots ,R$, are used to construct random walk proposals which are tailored to the shape of the tempered posterior distributions. The random walks for the different temperatures are performed independently and use a Gaussian mixture as proposal distribution, also known as small world proposal distribution (Fig. 1c). For a parameter vector ${\theta }_{\ell }^{\left[i\right]}$ in the rth region, ${\theta }_{\ell }^{\left[i\right]}\in {\Omega }_r$, the region-based proposal distribution is

$$q_{\ell ,r}^{\left[i\right]}\left({\theta }_{\ell }^{\prime }\right|{\theta }_{\ell }^{\left[i\right]})=(1-p_g\left)\mathcal{N}\right({\theta }_{\ell }^{\prime }|{\theta }_{\ell }^{\left[i\right]},e^{2{\eta }_{\ell ,r}^{\left[i\right]}}{C}_{\ell ,r}^{\left[i\right]})+p_g\mathcal{N}\left({\theta }_{\ell }^{\prime }\right|{\theta }_{\ell }^{\left[i\right]},e^{2{\eta }_{\ell }^{\left[i\right]}}{C}_{\ell }^{\left[i\right]}).$$ (5)

The mixture components capture the correlation structures of the tempered posterior ${\pi }^{1/{\tau }_{\ell }}\left({\theta }_{\ell }\right|\mathcal{D})$ in Ω_r and Ω, respectively. $C_{\ell ,r}^{\left[i\right]}$ and $C_{\ell }^{\left[i\right]}$ denote estimates of regional- and global covariance matrices while ${\eta }_{\ell ,r}^{\left[i\right]}$ and ${\eta }_{\ell }^{\left[i\right]}$ denote the scaling factors. The fraction of steps using the global proposal is denoted by p_g. The proposed points $\theta \prime \sim q_{\ell ,r}^{\left[i\right]}\left({\theta }_{\ell }^{\prime }\right|{\theta }_{\ell }^{\left[i\right]})$ are accepted with probability

$$p_{\text{acc}}=\min \left\{1,{\left(\frac{\pi \left({\theta }_{\ell }^{\prime }\right|\mathcal{D})}{\pi \left({\theta }_{\ell }^{\left[i\right]}\right|\mathcal{D})}\right)}^{1/{\tau }_{\ell }}\frac{q_{\ell ,r\prime }^{\left[i\right]}\left({\theta }_{\ell }^{\left[i\right]}\right|{\theta }_{\ell }^{\prime })}{q_{\ell ,r}^{\left[i\right]}\left({\theta }_{\ell }^{\prime }\right|{\theta }_{\ell }^{\left[i\right]})}\right\},$$ (6)

for region index $r\prime$ such that $\theta \prime \in {\Omega }_{r\prime }$. If accepted, ${\theta }_{\ell }^{[i+1]}={\theta }_{\ell }^{\prime }$, otherwise ${\theta }_{\ell }^{[i+1]}={\theta }_{\ell }^{\left[i\right]}$. Estimates for regional and global covariance are improved during the sampling phase. For ${\theta }_{\ell }^{\left[i\right]}\in {\Omega }_r$ updates of local mean and covariance are given by

$$m_{\ell ,r}^{\left[i\right]}=(1-{\gamma }^{\left[i\right]})m_{\ell ,r}^{[i-1]}+{\gamma }^{\left[i\right]}{\theta }_{\ell ,r}^{\left[i\right]},$$ (7)

$$C_{\ell ,r}^{\left[i\right]}=(1-{\gamma }^{\left[i\right]})C_{\ell ,r}^{[i-1]}+{\gamma }^{\left[i\right]}({\theta }_{\ell }^{\left[i\right]}-m_{\ell ,r}^{\left[i\right]}){({\theta }_{\ell }^{\left[i\right]}-m_{\ell ,r}^{\left[i\right]})}^T,$$ (8)

with adaptation strength ${\gamma }^{\left[i\right]}=i^{-\alpha }$, with $\alpha \in (0.5,1)$, and initial value obtained computed in the warm-up phase, $C_{\ell ,r}^{\left[0\right]}=C_r$. The scaling factors for regional and global covariance are adapted to achieve an acceptance rate of 23.4% (Haario et al., 2001; Łącki and Miasojedow, 2016): ${\eta }_{\ell ,r}^{\left[i\right]}={\eta }_{\ell }^{[i-1]}\hspace{0.17em}\text{exp}\hspace{0.17em}\left({\gamma }^{\left[i\right]}(p-0.234)\right)$ with ${\eta }_{\ell ,r}^{\left[0\right]}=1$.

The region-based random walk proposal is incorporated in a PT algorithm with an adjacent swap proposal and temperature adaptation. For the temperature adaptation the method by (Vousden et al., 2016) is employed and a maximum temperature ${\tau }_{\text{max}}$ is selected [for details see (Vousden et al., 2016)]. The temperatures of the sub-chains, $1={\tau }_1<{\tau }_2<\dots <{\tau }_L={\tau }_{\text{max}}$, are adapted such that swap acceptance for adjacent sub-chains is balanced:

$$\begin{array}{l}{\tau }_{\ell }^{\left[i\right]}=\sum _{m=2}^{\ell }\left({\tau }_m^{[i-1]}-{\tau }_{m-1}^{[i-1]}\right)\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-{\kappa }^{\left[i\right]}\left(A_m^{\left[i\right]}-A_{m-1}^{\left[i\right]}\right)\right\},\\ \text{with} {\kappa }^{\left[i\right]}=\frac{{\nu }_{\tau }}{{\eta }_{\tau }(i+1+{\nu }_{\tau })}\end{array}$$ (9)

for $\ell =1,\dots ,L$. The adaptation strengths are set ν_τ = 10³ and η_τ = 10 according to personal experience. $A_{\ell }^{\left[i\right]}$ indicates whether the proposed swap between chain $\ell$ and $(\ell +1)$ has been accepted. We note that the temperatures τ₁ = 1 and τ_L = τ_max are constant.

The resulting algorithm, RAmPART, is flexible as it possesses the RB-AM and the adaptive PT as special cases. A RB-AM is obtained for L = 1 and an adaptive PT for R = 1, respectively. As RAmPART meets the Diminishing Adaptation and the Simultaneous Uniform Ergodicity condition, results of (Roberts and Rosenthal, 2007, Theorem 5), ensures that it is ergodic and converges in distribution to the posterior. The pseudocode for the RAmPART algorithm can be found as part of the Supplementary Material.

2.3 Analysis pipeline

In this study, RAmPART is compared to different state-of-the-art algorithms. To ensure an unbiased comparison, we employed the semi-automated analysis pipeline described in a recent benchmark study (Ballnus et al., 2017). This pipeline facilitates the automatic identification of the burn-in phase, the robust analysis of convergence and the assessment of ESSs. For details on the analysis pipeline, we refer to the original publication (Ballnus et al., 2017).

2.4 Implementation

RAmPART is implemented in the MATLAB toolbox PESTO (Stapor et al., 2018), which is available on GitHub (https://github.com/ICB-DCM/PESTO/tree/RAmPARTSubmissionCode). The implementation of the considered benchmark and application problems are available as Supplementary Material. For the numerical simulation, we used the SUNDIALS toolbox CVODES (Serban and Hindmarsh, 2005) via the MATLAB interface AMICI (Fröhlich et al., 2017).

3 Results

To assess the performance and robustness of RAmPART, we used it to study two simulation examples as well as two biological problems. As a reference we considered own implementations of state-of-the-art RB-AM and adaptive PT algorithms.

To ensure that the results are representative, we performed 100 runs with 10⁶ iterations per algorithm and problem. The assessment is based on all these runs, which in total correspond to 18.000 CPU hours.

3.1 Simulation examples

To illustrate the properties of RAmPART, we considered two established benchmark problems: Gaussian mixture distributions (Łącki and Miasojedow, 2016) and blurred rings (Kramer, 2016). We studied a 20-dimensional Gaussian mixture distribution with two modes,

$${\pi }_{\text{gm}}(\theta |\mathcal{D})\propto \left(\sum _{i=1}^2\mathcal{N}\left(\left(\begin{array}{l}{\theta }_1\\ {\theta }_2\end{array}\right)|\left(\begin{array}{l}{\mu }_{i,1}\\ {\mu }_{i,2}\end{array}\right),\Sigma \right)\right)\prod _{j=3}^{20}\mathcal{N}({\theta }_j|25,{\sigma }^2),$$ (10)

and a 20-dimensional blurred ring,

$${\pi }_{\text{ring}}(\theta |\mathcal{D})\propto \mathcal{N}\left(r(\theta )|r_0,{\sigma }_r^2\right)\prod _{j=3}^{20}\mathcal{N}({\theta }_j|0,{\sigma }^2)$$ (11)

with $r(\theta )=\sqrt{{\theta }_1^{\mathrm{2}}+{\theta }_2^{\mathrm{2}}}$. For both benchmarks the distribution of the first to parameters are non-Gaussian, while the distribution of the remaining parameters is Gaussian (Fig. 2a and b). The precise parameterizations of the benchmarks are provided in the Supplementary Material.

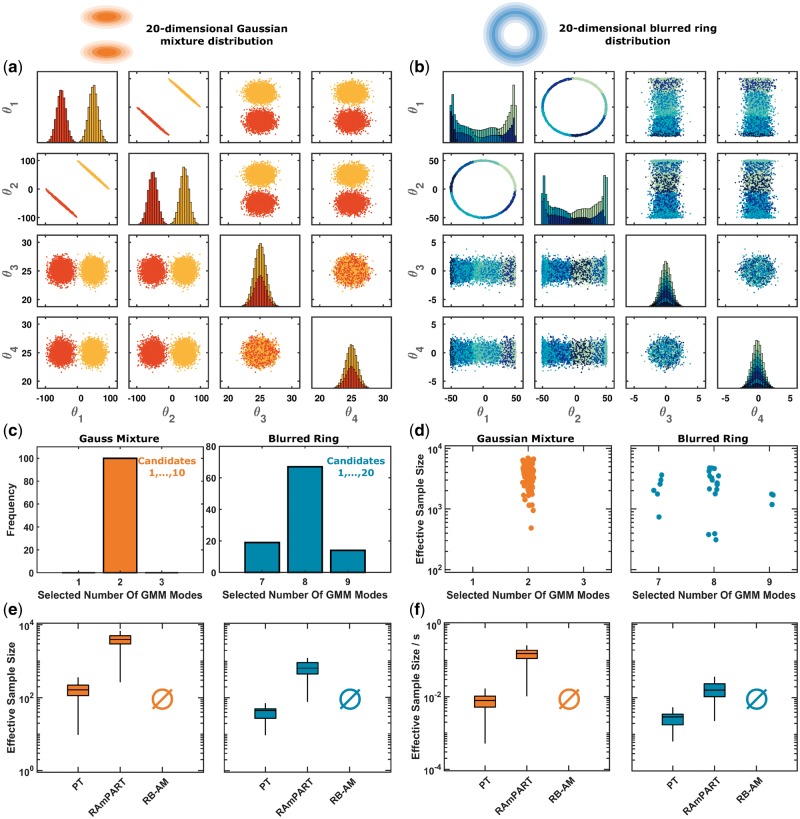
Fig. 2.

RAmPART outperforms established methods for simulation examples: 20-dimensional Gaussian mixture and the 20-dimensional blurred ring. (a and b) Bivariate scatter plot matrix and histograms for a representative chain generated using RAmPART. Parameters ${\theta }_1-{\theta }_4$ are illustrated. The parameters ${\theta }_5-{\theta }_{20}$ possess the same distribution as θ₃ and θ₄. (c) Variability of the selected GMM complexity between RAMPART runs. (d) The remaining ESS for different selected GMM complexities after application of the analysis pipeline. (e and f) Quantitative assessment of the ESS and the ESS per second computation time for different algorithms

We sampled the benchmark problems with RB-AM, PT and RAmPART. For PT and RAmPART, 40 temperature levels were employed. RAmPART was initialized with the last 50% of a PT run with 10⁵ samples. For this sample size, PT explored a large fraction of the parameter space but samples were not representative for the posterior distribution. However, the inference of GMMs using EM already provided reasonable definitions of regions [Fig. 2(a–d)].

As the number of regions and their location differed between runs, we assessed it and quantified its impact on the sampling phase. For the Gaussian mixture example, we found that the cross-validations always yielded two regions (Fig. 2c). For the blurred ring, on average eight regions were selected for the considered sample size (Fig. 2c). Here, the covariance matrices of regions differed substantially, which allowed for a good approximation of the distribution. For both examples, the sampling efficiencies were independent of the number of regions and their locations (Fig. 2d).

The evaluation of the sampling results revealed that RB-AM and PT suffer from convergence problems for the considered sample size (Fig. 2e and f). The RB-AM did neither provide representative samples for the Gaussian mixture nor for the blurred ring as it failed to explore the posterior. In most runs, PT provided a representative sample from the Gaussian mixture, but not for the blurred ring. RAmPART converged in 95 of 100 runs for the Gaussian mixture and in 25 of 100 runs for the blurred ring. The computation time per iteration was highest for RAmPART. Yet, due the decreased auto-correlation, the ESS was highest for RAmPART, both in absolute terms and relative to the computation time (Fig. 2e and f).

The comparison of PT and RAmPART revealed that the use of region-based random walk proposals (p_g = 0.5) improved convergence and computational efficiency. Accordingly, we wondered whether a pure region-based random walk proposal would perform even better (p_g = 1). Interestingly, this was not the case for the considered benchmark problems (Supplementary Fig. S1a). This indicates, that the small-world proposal used by RAmPART for p_g = 0.5 exploits benefits of local and global proposals and improves the overall robustness.

3.2 Application examples

To evaluate RAmPART in practice, we considered the processes of mRNA transfection and Epo-induced JAK2/STAT5 signaling:

• mRNA transfection is a promising treatment option, among others, in immunotherapy (Kuhn et al., 2011). In mRNA transfection, mRNA is encapsulated in lipoplexes, transported across the cell membrane, released into the cytosol and being translated (Fig. 3a). Single cell time-lapse data for this process have been collected and modeled by (Leonhardt et al., 2014; Fig. 3b). In this study, we consider the model introduced by (Leonhardt et al., 2014) inferring its five parameters from a representative single-cell trace.

• Epo-induced JAK2/STAT5 signaling is essential for survival, proliferation and differentiation in hematopoesis (Bachmann et al., 2014). Epo binds to the complex of the Epo receptor (EpoR) and JAK2. The complex induces phosphorylation of STAT5, which subsequently dimerises and translocates to the nucleus to regulate gene expression (Fig. 3c). An initial model of this process has been developed by (Swameye et al., 2003). Here, we consider the implementation of the model by (Maier et al., 2017) with 17 parameters and fit it to quantitative immunoblotting data (Fig. 3d).

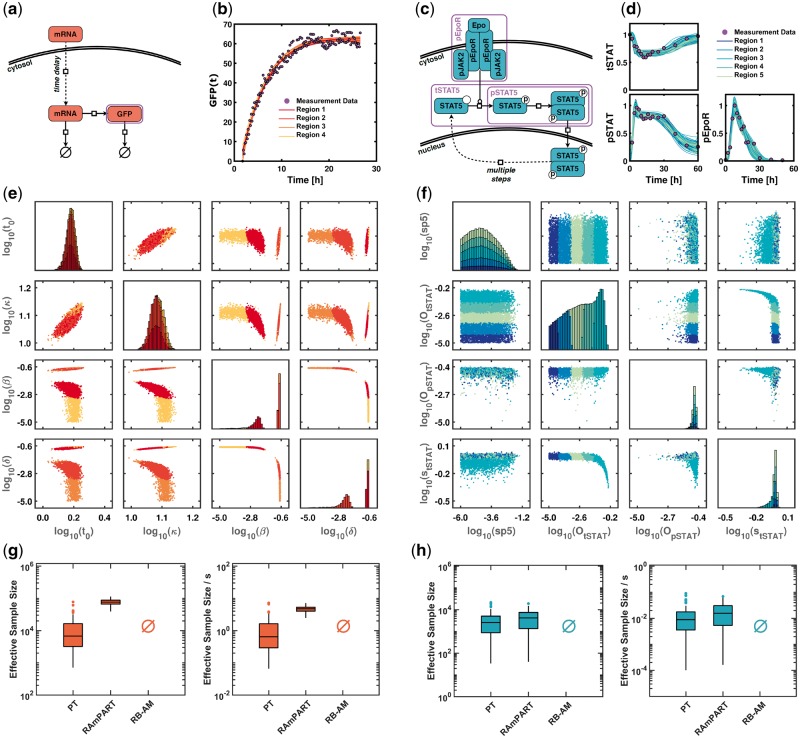
Fig. 3.

RAmPART adapts to the posterior landscape and outperforms established methods for models of mRNA transfection and JAK2/STAT5 signaling. (a) Biochemical reaction network for model of mRNA transfection. (b) Measurement data and propagated model trajectories of the observable G(t) derived from the parameter sample points. (c) Biochemical reaction network for model of JAK2/STAT5 signaling. (d) Measurement data and propagated model trajectories of the observables tSTAT, pSTAT and pEpoR derived from the parameter sample points. (e and f) Bivariate scatter plot of one RAmPART MCMC chain. The colors indicate the different regions. (g and h) Comparison of the ESS and the ESS per second computation time for the sampling algorithms

For both applications, log₁₀-transformed parameters were employed and uniform prior distributions were used. For details on the models and the experimental data, we refer to the Supplementary Material.

We sampled the posterior distributions of the models using RB-AM, PT and RAmPART with the same settings as for the simulation examples (Fig. 2). RAmPART provided the most representative sample of the posterior distribution, while especially RB-AM suffered from convergence problems. The trajectories contained in the representative samples by PT and RAmPART provide a good description of the experimental data (Fig. 3b and d).

The sampling results for the model of mRNA transfection revealed a bimodal posterior (Fig. 3e). Accordingly, in all runs RamPART selected at least two regions, on average 4.8. In all runs, the two modes were separated into different regions, allowing RAmPART to account for the different local correlation structures. Furthermore, each mode was often split into several regions to cover the tails (Fig. 3e). RAmPART identified the symmetry between the degradation rates, β and γ, on the level of the sample and the level of the regions. This symmetry is associated to structural identifiability problems. However, it can not be identified by established tools for structural identifiability analysis, such as GenSSI 2.0 (Ligon et al., 2017). The automatic identification of symmetries offered by RAmPART is important, as currently the analytical solution is required.

The sample for the model of JAK2/STAT5 signaling, did not reveal multi-modality as for the mRNA transfection but practical non-identifiabilities (Fig. 3f). Practical non-identifiabilities manifested as tails in the posterior distributions and were visible, among others, for ${\mathrm{O}}_{\text{tSTAT}}$ and ${\mathrm{s}}_{\text{tSTAT}}$. If these parameter dimensions are considered for the training of the GMM, RAmPART selects 4–5 regions. These regions partition the distributions and possess different correlations structure, facilitating the construction of a tailored proposal distribution.

Overall, our evaluation of the sampling performance and robustness revealed that RAmPART is more efficient than the established methods for both application problems (Fig. 3g and h). For mRNA transfection, RAmPART achieves a 6.6-fold higher ESS/t than PT (Fig. 3g). The key reason probably was the improved alignment of the regional proposal densities of RAmPART compared to the coverage of the two modes by the global proposal density of PT. For JAK2/STAT5 signaling, we found that RAmPART doubled the ESS/t in presence of a rather simple posterior structure (Fig. 3h). Apparently, even though the posterior structure is uni-modal, a GMM provide a substantially better approximation than a single Gaussian due to the pronounced tails of the posterior. This seems to allow RAmPART to outperform PT.

4 Conclusion

Computational models are an important tool in systems biology. The available information about model parameters, given experimental data, is encoded in the corresponding posterior distribution. The most common approach for comprehensive assessment of such a probability distribution is Markov-chain Monte–Carlo sampling. However, for computationally demanding problems with posterior distributions which possess multiple modes or pronounced tails, standard methods (i.e. the Metropolis Hastings or AM), are known to require massive computational resources in order to provide representative samples (Ballnus et al., 2017). Thus, MCMC sampling remains challenging and is subject to ongoing research.

Here, we proposed the region-based adaptive PT algorithm RAmPART, which adapts to the tempered posterior distribution and constructs tailored proposal densities on the fly. Following the requirements formulated by (Craiu et al., 2009, 1464–1465), this multi-level adaptation is designed to achieve good sampling properties ‘within each region’ and transition between ‘all regions’. While this manuscript did not provide new biological findings, it presented an algorithm which is suited for the ill-posed inference problems encountered in systems- and computational biology.

We evaluated the performance of RAmPART for benchmark and application problems. Our analysis revealed that RAmPART possesses a higher computation cost per iteration than RB-AM and PT, but it also provides a higher ESS. The increased computational cost is compensated by the improved mixing which resulted in a higher ESS per unit computation time. RAmPART outperformed the reference implementations of RB-AM and PT for all considered problems, by providing an improved ESS and a higher reliability of individual runs. Both aspects are highly relevant in practice and will allow for a consideration of higher-dimenional models with more involved posterior distributions. The results should be corroborated by analyzing a larger set of application problems.

The algorithm might be further improved by adapting the regions during the sampling, instead of fixing them after the warm-up phase. Ideas by (Craiu et al., 2009) might be employed, as implemented in the single-chain algorithm RAPTOR. Complementary, more robust clustering approaches could be used [e.g. (Gesteira Costa Filho, 2008; Levenstien et al., 2003)] to enhance the robustness of RAmPART. Alternatively, instead of using region-based proposal densities, Hamiltonian Monte–Carlo methods (Graham and Storkey, 2017; Hoffman and Gelman, 2014) might be employed for the different temperatures.

In summary, we introduced RAmPART and provided a comprehensive evaluation. The proposed algorithm has substantial practical value and is publicly available in the MATLAB toolbox PESTO. This will facilitate its reuse and application to a broad class of problems.

Funding

This project has received funding through the European Union’s Horizon 2020 research and innovation program under grant agreement no. 686282, and the Post-doctoral Fellowship Program (PFP) of the Helmholtz Zentrum München.

Conflict of Interest: none declared.