Abstract
The performance of a molecular motor, characterized by its power output and energy efficiency, is investigated in the motor design space spanned by the stepping rate function and the motor-track interaction potential. Analytic results and simulations show that a gating mechanism that restricts forward stepping in a narrow window in configuration space is needed for generating high power at physiologically relevant loads. By deriving general thermodynamics laws for nonequilibrium motors, we find that the maximum torque (force) at stall is less than its theoretical limit for any realistic motor-track interactions due to speed fluctuations. Our study reveals a tradeoff for the motor-track interaction: while a strong interaction generates a high power output for forward steps, it also leads to a higher probability of wasteful spontaneous back steps. Our analysis and simulations show that this tradeoff sets a fundamental limit to the maximum motor efficiency in the presence of spontaneous back steps, i.e., loose-coupling. Balancing this tradeoff leads to an optimal design of the motor-track interaction for achieving a maximum efficiency close to 1 for realistic motors that are not perfectly coupled with the energy source. Comparison with existing data and suggestions for future experiments are discussed.
PACS numbers: 87.16.Nn, 05.70.Ln, 87.16.Qp, 87.17.Jj, 87.19.lu
I. INTRODUCTION
Molecular motors are essential for living systems. They convert chemical energy to mechanical work driving motion and transport in biological systems. While linear motors such as kinesin and myosin are fueled by ATP, bacterial flagellar motor (BFM) couples ion (e.g., H+ and Na+) translocations across cytoplasmic membrane to the rotation of flagellar filaments which propel the bacterial motion (tumbling or swimming) [1–4]. A fundamental question is whether there are thermodynamic bounds to the power generation and energy efficiency for these highly non-equilibrium molecular engines [5–7]. A related and perhaps more important question is what are the microscopic properties (design features) that would allow a molecular motor to approach these bounds under realistic constraints. Here, we try to address these general questions and test the findings in the specific case of BFM, which is believed to be highly efficient.
We first describe briefly what is known about the bacterial flagellar motor (see [8] for a recent review). The rotor of this nanoscale rotary engine contains a ring of ~ 26 FliG proteins (see [9] for an alternative view of 34 FliGs in the rotor), which serve as the track of the engine and interact with multiple torque-generating stator units that are anchored to the cell wall. In E. coli, each stator unit is composed of four copies of MotA and two copies of MotB, forming two transmembrane proton channels [10–16]. Ion translocations through the channels cause conformational changes of the stator proteins which generate torque on the rotor to drive its rotation [17, 18]. The ion flow is powered by the ion motive force (IMF), which is the free energy difference of an ion across the cell membrane. IMF depends on the transmembrane voltage and the ion concentration difference across the cytoplasmic membrane. For E. coli, the responsible ion is proton, and the driving force is the proton motive force (PMF).
The mechanical properties of the flagellar motor, characterized by its torque-speed relationship, have been measured experimentally under various conditions (e.g., different PMF, temperature, number of stators) [19–22]. For E. coli, the torque-speed dependence for a BFM in the counterclockwise (CCW) rotational state has a concave down shape, with a plateau of high torque at low speeds and a rapid drop of torque at high speeds. On the other hand, the torque-speed curve for the clockwise (CW) motor is almost linear [23]. Based on specific choices of the stator-rotor interaction and the energy transduction process, several models have been developed to explain the observed torque-speed relationship for the BFM [24–32].
Our understanding of the thermodynamics and energetics of BFM remains limited. Some experiments suggested that BFM is tightly coupled, meaning that a fixed number of ions pass through the motor per revolution [33, 34]. It was argued that since at high loads the motor moves slowly and thus operates near equilibrium with the thermal bath, the efficiency should be close to one [35]. However, recent experiments by Lo et al. [36] found that the maximum torque generated near stall is approximately equivalent to the energy provided by only 37 ± 2 ions per revolution, which is smaller than the previous estimate of 52 ions, given 26 FliG in the rotor and two ions per FliG step [37–39].
For modeling molecular motors, the Brownian ratchet models have long attracted physicists’ attention since Richard Feynman popularized it a half century ago [7, 40–42]. Among all variants of the ratchet models (see [6] for a review), only the isothermal chemical ratchets [43] are relevant for biological motors. The efficiency of isothermal ratchets can reach 100% under ideal conditions near equilibrium when the speed goes to zero (stall) [5]. However, the power output vanishes at this ideally efficient point, which motivates researchers to study efficiency at maximum power [44, 45]. Another serious shortcoming of the idealized models is that realistic biological motors are under constraints on the motor-track interaction potential as well as the reversibility of the underlying chemical transitions, which can have significant effects on motoor performance. In fact, it was already realized in [5] that instead of being 100% the efficiency actually vanishes at stall if spontaneous stepping transitions are included, which leaves the maximum efficiency under biological constraints an open question.
In this paper, we address the general question on how realistic microscopic properties of the motor, such as the shape of the motor-track interaction potential, the degree of irreversibility in mechano-chemical transitions, and the gating (control) of the stepping transitions affect the motor performance (efficiency, power, and maximum torque (force) generation). We do so by developing a minimal stochastic motor model where both energy-assisted and spontaneous stepping transitions are included. The motor dynamics are determined by two intrinsic mechanochemical functions: 1) the interaction potential of the power generating motor molecules (kinesin, myosin, or MotAB) and their counterpart track molecules (microtubule, actin, or FliG), 2) the stepping rate function that depends on the relative motor-track coordinate. Together, these two microscopic functions constitute the “design” space of molecular motors. We study general thermodynamic properties of molecular engines by exploring this motor design space, where a specific motor such as BFM corresponds to one particular region. Our approach not only allows us to gain important insights on the specific molecular mechanisms for the observed properties (e.g., the torque-speed relationship for BFM). More importantly, exploring the motor design space reveals fundamental thermodynamic bounds for all realistic molecular engines and general design principles to approach these bounds.
II. A MINIMAL MODEL FRAMEWORK FOR MOLECULAR MOTORS
The approach and terminology for the minimal motor model are based on previous modeling work on BFM [26, 28], but the general formalism can be applied to other motor systems. As illustrated in Fig. 1, the interaction between stator and rotor drives the rotation of the rotor from a high potential energy position towards its equilibrium position (with the lowest potential energy). The passage of an ion enhances a stator conformational change (stepping), which brings the motor to a new stator-rotor potential where the motor is again in a high potential energy state. The newly gained potential energy continues to drive the (physical) rotation of the rotor. This continuous process drives the system towards a sequence of new equilibrium positions and gives rise to a directed stepwise rotation [37].
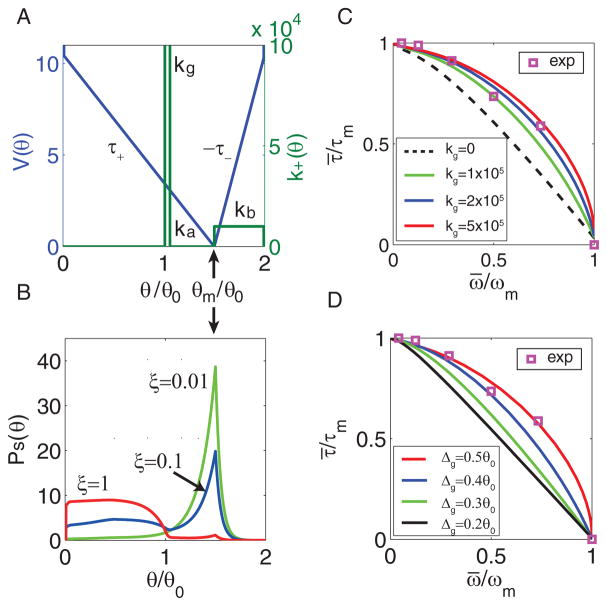
FIG. 1.
Illustration of the minimal motor model. (A) The motor is described by its motion (red arrows) in physical space (angle θ) along the interaction potential V (θ). The gray box highlights the forward and backward stepping transitions, represented by the solid and dotted green arrows respectively, between two adjacent potentials (black and blue lines) shifted by half a period θ0. A V-shaped potential is shown with its minimum at (1+ε)θ0 and depth Vd. An energy barrier VB(θ) is added to prevent back flow. (B) There are two types of chemical transitions highlighted in the gray box in (A): the PMF-coupled transitions (red arrowed lines) and the spontaneous transitions (gray arrowed lines). Detailed balance is broken in the reaction loop which leads to a dissipative reaction cycle. Forward and backward reactions between state-1 to state-2 are represented by solid and dotted lines, respectively. (C) The chemical transitions shown in the chemical conformation space. The ratio between the total forward rate (k+) and the total backward rate (k−) depends on the energy gap Eg, which is the difference between the effective driving energy G0 and potential gain ΔV (θ).
A. The Fokker-Planck equation
For a processive motor like BFM with a high duty ratio, the motor dynamics can be described by two stochastic processes: 1) the physical motion (rotation), which can be viewed as a particle sliding along an energy potential V(θ) with thermal fluctuations; 2) the chemical transitions (“stepping”), which correspond to hoping between neighboring energy potentials shifted by half a period θ0. For BFM, the stator-rotor interaction potential V (θ) has a periodicity 2θ0 ≡ 2π/26, where θ ≡ θR− θS is the relative angle between the stator angle θS (“chemical” coordinate) and the rotor angle θR (“physical” coordinate). For a linear motor like kinesin, V represents the kinesin-microtubule interaction potential with a period of ~ 8nm [46].
Following [26], we study the probability distribution function P(θ, t) for θ by using the Fokker-Planck (FP) equation:
| (1) |
with ω the angular speed, ξ the viscous drag coefficient, and kBT the thermal energy set to 1 hereafter. In sub-cellular environments, motor dynamics is over-damped and the motor speed (ω) is proportional to torque: ω = τ/ξ = (−V′(θ)+τext)/ξ, where τext is an external torque applied in the opposite direction of the motor rotation, ξ is the viscous drag coefficient (load).
The first term on the right hand side of Eq. (1) is the probability flux due to continuous physical motion. The second term Δjs(θ) is the net flux due to stepping:
| (2) |
where the forward and backward stepping fluxes are given by j±(θ) = k±(θ)P(θ) with k+(θ) the forward rate of leaving from θ to (θ − θ0) and k−(θ − θ0) the rate of jumping back to θ from (θ − θ0). For simplicity, we assume k+(0 < θ < θ0) = 0 and k− (2θ0 > θ > θ0) = 0. See Sec. A and Fig. 7 in the Appendix for details of the model derivation.
FIG. 7.
Illustration of transitions between states in different energy landscapes shifted by the IMF (G0). The black line represents the state 1 with potential V1(θ) = V (θ). The blue lines represent the two adjacent states (2′ and 2) with potentials V2(θ) = V (θ+θ0) shifted by G0 and −G0 for state 2′ and state 2 respectively, θ0 is the half period. The green arrowed lines represent the transitions between the states with the transition rates labeled (see Appendix A for details). Due to symmetry, the transition rates (k2′1 and k12′) between states 2′ and 1 are the same as the transition rates (k12 and k21) between states 1 and 2 with the angle θ shifted by θ0.
B. Irreversible chemical cycle and loose coupling
There are two distinct pathways for chemical transitions (Fig. 1B). For the PMF-coupled transitions, the forward transition is boosted by the PMF energy E0 (E0 is the ATP hydrolysis energy for linear motors), and the backward transitions regain the energy by pumping a proton out (or synthesizing ATP). The transition rates satisfy the thermodynamic constraint: k+,i(θ) = e−ΔV + E0k−,i(θ − θ0) where ΔV ≡ V (θ − θ0) − V (θ) is the potential energy change (gain) for a forward step. There are also spontaneous transitions that are decoupled from the energy source, their rates satisfy: k+,s(θ) = e−ΔV k−,s(θ − θ0). In the presence of both types of transitions, we have , which indicates that detailed balance is broken between the chemical states (with the same physical coordinate θ). Therefore, some of the PMF energy is dissipated by the irreversible chemical reaction cycle (see Fig. 1B) without driving any physical motion. This loss of energy prevents the system from being 100% efficient.
The relative strength of the two types of stepping transitions can be characterized by a reversibility parameter κ: k−,i = κk−, k−,s = (1 − κ)k−. The ideal case of κ = 1 corresponds to the perfectly tight-coupling scenario where every forward step transition is powered by the cheminal energy and every back step transition regains the chemical energy (pump out H+ or synthesize ATP). However, most realistic molecular motors are loosely coupled (not perfectly tight-coupled) with 0 < κ < 1. For example, both myosin and kinesin have a net ATP hydrolysis rate at stall [47, 48] and some backward steps can even cost energy [49]. A loose coupling mechanism is also proposed recently for BFM [31]. One of the goals of our study is to search for design principles to enhance motor performance under the realistic constraint of only partially reversible κ < 1.
Combining the two types of stepping transitions, the total transition rates k±(= k±,i + k±,s) satisfy:
| (3) |
where G0 ≡ ln(1−κ+ κeE0) is the effective driving energy. Except for cases with extremely small κ (we use κ = 0.5 in this paper unless otherwise stated), we have G0 ≈ E0 + ln(κ) ≈ E0 when − ln κ ≪ E0.
As shown in Fig. 1C, An energy “gap” Eg ≡ G0 − ΔV is defined to characterize the difference (gap) between the effective driving energy G0 and the potential energy gain ΔV. From Eq. (3), a positive energy gap (Eg > 0) suppresses the back steps, which is crucial for enhancing motor efficiency as we show later in the paper. As defined, Eg is θ-dependent. Here, we use it to denote the energy gap at where k+ is the highest.
C. Approach and general model behaviors
Eqs. (1–3) completely define a minimal thermodynamically consistent model for molecular motors, including linear motors like myosin, where the coordinate θ would represent the relative positional difference between myosin and actin. The steady state distribution Ps(θ) is determined by solving the steady state FP equation:
| (4) |
with periodic condition Ps(θ) = Ps(θ+2θ0) and normalization . The intrinsic properties of the motor are characterized by two functions: the interaction potential functions V (θ) and stepping rate function k+(θ) (k−(θ) is given by Eq. (3)). The external load is determined by ξ.
For a given load ξ, Eq. (4) can be solved to obtain Ps(θ), from which the average torque generated by the motor can be determined: , and the average (rotational) speed can be obtained by the over-damped assumption valid at low Reynolds number: ω̄(ξ) = τ̄(ξ)/ξ. By sweeping through different values of ξ, the model results in a torque-speed (τ̄ − ω̄) relationship, which can be compared directly with experiments. The maximum torque τm is reached at high-load (ξ → ∞) when the motor is at stall (ω̄ = 0).
In the absence of external energy source and external force, i.e., when E0 = 0 and τext = 0, the system is in equilibrium with its thermal environment. It is easy to show that the steady-state solution for Eq. (1) in this case is simply the equilibrium Boltzmann distribution: Ps(θ) = Ω−1 exp[−V (θ)], with the normalization constant. Consequently, there is no net torque generation or motion, i.e., ω̄ = τ̄ = 0.
However, when E0 > 0, detailed balance is broken between different physical coordinates (θ), i.e., k+(θ)Ps(θ) ≠ k− (θ − θ0)Ps(θ − θ0), and the motor can generate a nonzero average torque to drive mechanical motion (rotation). The viscous drag ξω̄ is considered as the natural load on the motor. Even though an external torque τext can also be applied to probe the motor behaviors, it is more convenient and biologically more realistic to change the load by varying ξ as done by almost all experiments on BFM. For the remaining of this paper, we set τext = 0 and varying ξ except when we discuss different definitions of the motor efficiency at the end of the paper.
III. DESIGN PRINCIPLES FOR OPTIMAL MOTOR PERFORMANCE
In the general model framework given in the last section, the motor design space is spanned by two intrinsic functions: V (θ) and k+(θ). For a specific motor system like BFM, specific choices of V (θ) and k+(θ) were made to fit experimental data and backward transitions k− (θ) were typically neglected. Here, we treat k+(θ) and V (θ) as a variable functional, and we always keep k− (θ), which is determined from k+(θ) and V (θ) by using Eq. (3). By systematically exploring the motor design space, our main goal is to investigate fundamental limits and possible design principles for optimal motor performance characterized by its power output and energy efficiency for a given driving energy E0.
A. A gating mechanism for high power generation
The average power output of the motor, defined as Ẇ = τ̄ω̄, can only be high if both τ̄ and ω̄ are high. The measured torque-speed curve for CCW BFM has a concave down shape with a roughly constant high torque at low to medium speeds and a fast decrease of torque at high speeds [22, 36]. This concave torque-speed curve has the advantage of generating high power output (or equivalently a high torque for a given speed) in a wide range of physiologically relevant loads. Here, we study the general design requirements for such a concave torque-speed dependence, which is critical for high power generation.
The form of the periodic potential V (θ) is characterized by two parameters: the depth of the potential Vd, and the location of its minimum θm ≡ (1+ε)θ0, where ε ∈ [0, 1] is an asymmetry parameter. A symmetric potential corresponds to ε = 0, and ε = 1 represents the extreme case when the potential is infinitely steep at θ = 2θ0. For simplicity, we used a piece-wise linear form (V -shaped) for V (θ) for most of the paper as shown in Fig. 1A and Fig. 2A. Other forms of V (θ), such as parabolic functions, were also used without affecting the main results (see Section C and Fig. 9 in Appendix for details). For the V - shaped potential, the torque generated from this potential is positive τ (θ) = τ+ ≡ Vd/θm > 0 for 0 ≤ θ < θm, and negative τ (θ) = −τ− ≡ − Vd/(2θ0 − θm) < 0 for θm < θ ≤ 2θ0, as shown in Fig. 2A. A high energy barrier VB near the peak of V (θ) is also added to prevent slipping between two adjacent FliG’s without stepping. A piece-wise linear form of VB is used (see Appendix B). In the following, we focus on elucidating the role of controlling (gating) the stepping transitions, i.e., the specific form of k+(θ), for obtaining the observed torque-speed characteristics and high power generation.
FIG. 2.
The motor probability distribution and the gating effect on the torque-speed curve. (A) The stator-rotor interaction potential V (θ) (blue line); and the forward stepping rate k+(θ) (green line). A positive torque τ+ is generated when θ < θm and a negative torque −τ− is generated when θ > θm. (B) The steady-state distribution Ps(θ) at three representative loads: high load ξ = 1 (red), medium load ξ = 0.1 (blue), and low load ξ = 0.01 (green) for kg = 5 × 105 with V (θ) and k+(θ) given in (A). Note that the peak of Ps(θ) at the bottom of potential θm, indicated by the arrows in both (A) and (B), increases as the load (ξ) decreases. (C) The torque-speed curves for different values of the gating strength kg. The concavity increases with the gating strength kg. (D) The torque-speed curves for different values of the distance Δg ≡ θm − (θ0 + θε) between the gate and the potential minimum. The concavity increases with Δg. The square symbols in both (C)&(D) represent data from [36] (pH=7.0, [Na]ex = 30mM).
1. An analytical solution for the torque-speed relationship
We derive an approximate analytical solution for the torque-speed curve from our model based on ideas introduced before [28, 32]. At a microscopic timescale, the motor moves in two alternating modes: moving and waiting. The moving phase corresponds to the duration when the motor moves down the potential V and generates a positive torque τ+(> 0). The average moving time is approximately 〈tm〉 ≈ ξθ0/τ+. The waiting phase begins when the motor reaches the potential minimum θm. The waiting phase may be skipped due to stepping and the probability of reaching the potential minimum is pw = exp(−ξK/τ+), where is the integrated forward stepping rate over [θ0, θm]. Once reaching θm, the motor fluctuates (due to thermal noise) around θm “waiting” for the next stepping transition to occur. During the waiting phase, the system approximately follows the equilibrium distribution Ps(θ) ≈ Ω−1 exp[−V (θ)]. So the average waiting time , where is the average stepping rate in the waiting phase. By combining these considerations, we obtain an approximate solution for the speed ω̄ ≈ θ0(〈tm〉 + pw〈tw〉)−1. By introducing a re-scaled torque τ̃ ≡ τ̄/τ+ and a re-scaled speed ω̃ ≡ ω̄/ωm with ωm(= k0θ0) the maximum speed, we obtain an approximate analytical expression for the torque speed curve:
| (5) |
with a single parameter q that depends on V (θ) and k+(θ):
| (6) |
The concavity of the torque-speed curve is determined by q. For q → 0, torque-speed curve is linear τ̃ + ω̃ = 1 with zero concavity. As q increases, the concavity increases.
What is the design of k+(θ) that gives rise to a large value of q for a given V (θ)? The answer is revealed by Eq. (6). For the V -shaped potential, the dependence of K and k0 on k+(θ) shows that higher stepping rates in a narrow region away from the potential minimum can increase K without increasing k0 too much and thus lead to a larger value of q. This “gating” region characterized by a small width θg(≪ θ0) and a large stepping rate kg(≫k0) within the interval (θ0, θm) but closer to θ0, serves to prevent the motor from entering the waiting phase at high loads without increasing the maximum speed at low loads. These effects of the gating mechanism lead to the observed concavity in the torque-speed curve.
2. Simulation results
We verified this gating mechanism by direct numerical simulations. For simplicity, we choose a piecewise constant profile for k+ as shown in Fig. 2A: 1) k+(θ) = kg for θ ∈ [θ0 + θε, θ0 + θε + θg); 2) k+(θ) = ka for θ ∈ [θ0+θε + θg, θm); 3) k+(θ) = kb for θ ∈ [θm, 2θ0− θε); and zero otherwise. Here, θε(> 0) controls the gate location, θg and kg are the width and stepping rate of the gate region, ka and kb represent the background stepping rates to the left and right of the potential minimum, respectively.
For a given k+(θ), we solve Eq. (4) numerically to determine the steady state distribution Ps(θ) for any given load ξ. As shown in Fig. 2B, at high (ξ = 1, red line), Ps(θ) is mainly concentrated in the positive-torque region due to the gating effect, while it shifts to mostly populate around the potential bottom (θm) at low load (ξ = 0.01, green line), and it behaves somewhere in between for intermediate load (ξ = 0.1, blue line). We have computed the torque-speed curve for different values of kg. As shown in Fig. 2C, the concavity disappears as kg decreases. Note that for flagellar motor, we usually plot torque versus speed instead of speed versus external applied force as typically done in the linear motor case. The positioning of the gate is also studied. The concavity increases as the gate is moved away from the potential minimum at θm towards the midpoint at θ = θ0, i.e., as Δg ≡ θm − (θ0 + θε) increases, as shown in Fig. 2D. The dependence of the concavity of the torque-speed curve on the strength and position of the gate, as shown in Fig. 2C&D, agrees with our analytical results.
The normalized torque-speed curve with a strong gating strength and proper positioning (the red lines in Fig. 2C&D) agrees with experimental data [36] for the CCW BFM (square symbols in Fig. 2C&D). The predicted dependence of concavity on the gating mechanism also provides a possible mechanism for the CW motor, which shows a linear torque-speed curve [23]. These predicted dependence may be tested by future experiments that measure the torque-speed curve in cells with mutated residues around their ion channel [50, 51].
B. The maximum torque at stall is limited by speed fluctuations
Another important characteristic of any molecular motor is the maximum torque τmax (or maximum force for a linear motor) that the motor generates near stall. For a given G0, we ask the question what is the best design of V (θ) that optimizes τmax. Naively, it may be desirable to have a steep interaction potential to generate a large τmax. In the case of the V -shaped potentials, one would expect τmax to increase with the gradient (τ+) of the potential. We have computed τmax in our model for different choices of τ+. Surprisingly, as shown in Fig. 3A, although τmax increases with τ+ for small τ+, it reaches a peak value at a finite and decreases sharply for .
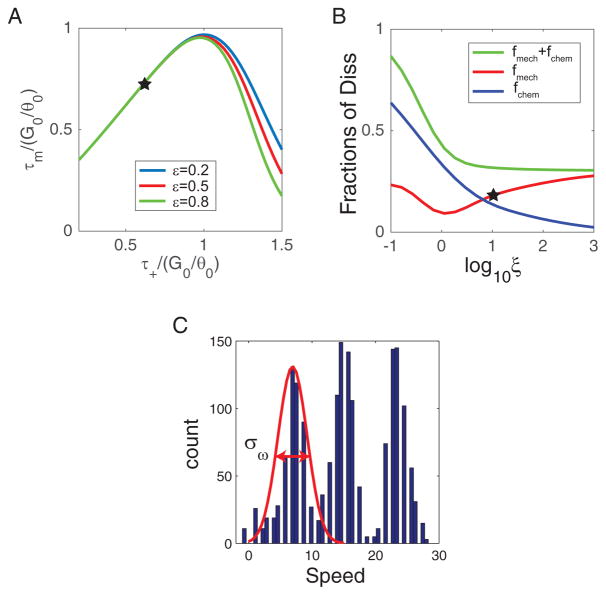
FIG. 3.
Maximum torque τm and the energy dissipations. (A) τm depends non-monotonically on the potential gradient τ+ for different values of ε = 0.2, 0.5, 0.8. The experimentally measured τm and its corresponding τ+ is marked by the star. (B) Fractions of energy dissipation due to torque (speed) fluctuations fmech (red line) and entropy production in chemical reactions fchem (blue line) versus load (ξ). fmech dominates at high loads, fchem dominates at low loads. The total dissipation (fmech + fchem) is shown as the green line. (C) The experimentally measured speed distribution when hook-only motors were attached to a large 1μm polystyrene bead with an estimated high load of ξ ≈ 8 (see [36] for details). The variance around the first peak σω corresponds to the speed fluctuation for motors with a single stator. The fractional dissipation due to speed fluctuation at ξ = 8 can be estimated fmech ≈ 0.16 (marked as a star) from (C). The original data are kindly provided by Dr. C-J Lo [36].
What causes this non-monotonic dependence of τmax on τ+? For a larger value of τ+, the torque generated in the positive torque regime (θ < θm) is larger. However, the backward stepping rate is also higher as the energy gap Eg = G0 − τ+θ0 is lower. The higher backward stepping rate increases the probability in the negative torque regime (θ > θm) and thus decreases the average torque (see Appendix C and Fig. 8 for details). These two competing effects of varying τ+ lead to the existence of a maximum τmax. Different choices of ε only change the peak slightly without changing the general behavior of τm (Fig. 3A).
FIG. 8.
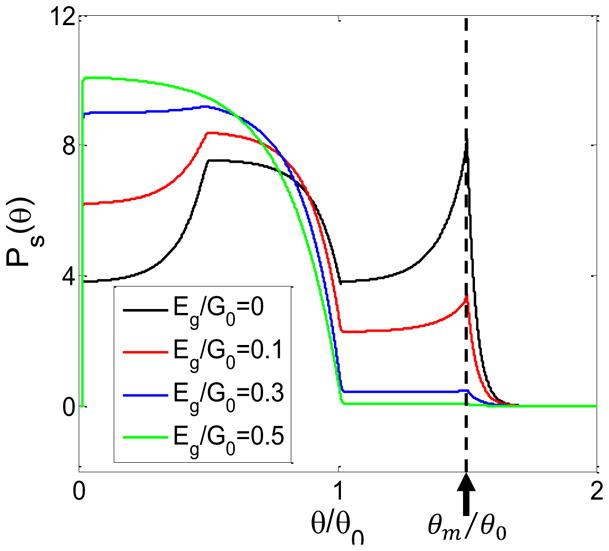
The distribution Ps(θ) for different values of Eg (by varying Vd and fixing ε = 0.5). The functions V (θ) and k+(θ) are the same as shown in Fig. 1C in the main text. The probability in the negative torque regime decreases with increasing Eg and thus the probability in the positive toque regimes P+ = 1−P− decreases with decreasing Eg.
1. Thermodynamic laws for molecular motors
The bound for τmax can be obtained rigorously by studying the thermodynamic torque τl(θ) = −(V (θ) + ln Ps(θ))′, where the first term represents the torque from the stator-rotor interaction and the second term is the “entropic” torque from thermal fluctuations akin to the thermodynamic pressure. By integrating the steady state Fokker-Planck equation, we obtain the average τι:
| (7) |
where are the total forward and backward fluxes. The second moment of τι can be computed: , where boundary terms are set to zero. In steady state, Eq. (1) leads to: . By using Eq. (4) for Δjs and Eq. (7) for τ̄, we have:
| (8) |
where is the entropy production rate of the chemical reactions.
In steady state, the power output or the rate of mechanical work performed by the motor (against viscous drag) is Ẇ ≡ ω̄τ̄. Using Eq. (8), we derive an equation for Ẇ:
| (9) |
where is the variance of the thermodynamic torque.
Eq. (9) is the first law of thermodynamics for a nonequilibrium motor system with an external energy source. The left hand side of Eq. (9) represents the rate of energy input. The first term on the right hand side (RHS) of Eq. (9) represent the average power output. In addition, there are two distinct sources of energy dissipation. Sj is the energy loss due to entropy production and the corresponding heat generation in chemical space. ξ−1στ is the energy dissipation due to fluctuations of torque and speed in physical space. We note that the speed and torque fluctuations depend on the nonequilibrium motor dynamics (driven by G0) in addition to thermal noise. In particular, the torque fluctuation στ is finite even when temperature goes to zero.
The second law of thermodynamics for the motor manifests itself by the fact that these two energy dissipation rates are positive definite:
| (10) |
From the first and second law, Eqs. (9–10), it follows that the average torque is bounded:
| (11) |
2. Simulation results and experiments
The question now is whether the maximum torque τmax can ever reach this theoretical limit G0/θ0. At high load ξ ≫ 1, the entropy production rate is small Sj ∝ ξ−2 because both and [j+(θ+θ0)−j−(θ)] ∝ ξ−1. However, in general στ does not vanish in the high load limit. The torque variance στ depends on the shape of V (θ) and only approaches zero when the interaction potential takes the extreme limit of ε → 1 with delta-function energy barrier. Given the size of a motor protein (~ 4nm) and that of a typical amino acid (~ 0.8nm), the asymmetry parameter should be ε < 1–0.8/(2×4) = 0.9. Therefore, any realistic form of V (θ) results to a finite στ and thus a maximum torque that is less than G0/θ0.
We have computed τ̄, ω̄, στ, and Sj for different load (ξ) in our model numerically. The fraction of energy dissipation through speed fluctuation and entropy production are given by fmech ≡ στ/(ξω̄G0/θ0) and fchem ≡ Sj/(ω̄G0/θ0), which are shown in Fig. 3B as red and blue lines respectively. Consistent with our analysis, the dissipation due to speed fluctuation fmech reaches a nonzero constant as ξ → ∞ while the dissipation from entropy production fchem → 0.
In the recent experiments by Lo et al. [36], the maximum torque near stall was found to be . From our analysis, this means that at least 29% of IMF is dissipated, and an increasing portion of the dissipation is caused by speed and torque fluctuations as the load increases (see red line in Fig. 3B). In Fig. 3C, the experimentally observed speed distribution at a high load (1μm bead) [36] is shown. Consistent with our analysis, significant speed fluctuations are present. Quantitatively, the average and variance of motor speeds for the motors with a single stator (those speeds around the first peak in Fig. 3C) are estimated to be ω̄ ≈ 6.5Hz and σω ≈ 6.4Hz2. The fraction of energy dissipation due to speed fluctuation can be estimated: στθ0/(τ̄G0) ≈ σω/ω̄2 ×τmaxθ0/G0 ≈ 6.4/6.52 ×0.71 = 0.11, which is in the same range but lower than the value 0.16 obtained from our model at the corresponding load (marked by a star in Fig. 3B). The reason for this quantitative difference may be that the model result depends on the detailed shape of V (θ), which is not tuned in this study. Additionally, σω may be an underestimate of the instantaneous speed fluctuation due to the experimental averaging process. Future experiments with high temporal resolution are needed to measure dynamics of the instantaneous speed fluctuation and to compare it directly with our model prediction in order to understand the microscopic origin of speed fluctuation and energy dissipation.
C. Performance limits in loosely coupled motors (κ < 1)
The motor’s power output is given by Ẇ = ω̄τ̄ = θ0(J+ − J−)τ̄. To determine the motor efficiency, we need to know the net free energy cost. Since only the proton-assisted transitions k±,i are coupled with energy consumption and regeneration, the average net energy consumption rate is: ΔG(κ) = E0(J+,i − J−,i) ≈ E0(J+ − κJ−), where we have neglected the much smaller spontaneous forward flux J+,s = (1 − κ)e−G0J+ ≪ J+. The motor efficiency can then be defined accordingly:
| (12) |
1. Maximum efficiency occurs at a finite speed with a positive energy gap
We have computed both the power output (Ẇ) and efficiency (Λ(κ)) in our model for different choices of interaction potential V (θ) characterized by Eg (equivalently τ+ or Vd). As expected, Ẇ = τ̄ × ω̄ reaches its maximum value Ẇm at a finite load (or a finite speed) and a positive energy gap Eg > 0. Surprisingly, however, for a loosely coupled motor with κ < 1, the efficiency Λ shows a similar behavior with its maximum at a finite load (or finite speed) as shown in Fig. 4B.
FIG. 4.
Power and efficiency of the motor. The dependence of (A) power, and (B) efficiency (for κ = 0.5) on energy gap Eg and load ξ. Both power and efficiency peak at an intermediate load and Eg, labeled by the blue dot (for power) and the black star (for efficiency). The red arrow indicates the Eg/E0 ≈ 0.29 estimated from experiments [36], which is close to the optimal Eg/E0 ratios for maximum power (blue dot) and maximum efficiency (black star). (C) Efficiency Λ versus normalized speed for different values of κ. Λ vanishes at ω̄ = 0 for all values of κ < 1. (D) The efficiency of the motor working at maximum power (blue line) is comparable to the (global) maximum efficiency Λ* (black line), with their ratio (red line) ~ 80% for a wide range of E0.
The efficiency-speed dependence is further studied for different values of κ. As shown in Fig. 4C, for high speeds (or low loads) Λ is independent of κ and decreases with speed. A strong dependence on κ occurs at low speeds (high loads). For any value of κ < 1, instead of reaching its maximum at zero speed, the efficiency vanishes linearly with speed. Only in the singular case of κ = 1, does Λ reach its maximum value at zero speed. In any loose-coupling motors (κ < 1), the efficiency Λ reaches its maximum at a finite speed. This is a much more “useful” maximum efficiency as the power output can also be high unlike the case of the purely reversible motor with κ = 1 where the maximum efficiency occurs at zero power.
To determine whether the motor can operate in a regime with both high efficiency and high power, we computed the efficiency at the maximum power, Λ(Ẇ = Ẇm), and the global maximum efficiency Λ* in our model for different E0 (Note that we explore the whole range of load and power output instead of just focusing on the efficiency at the maximum power [42]). As shown in Fig. 4D, the ratio, Λ(Ẇm)/Λ*, is as high as about 80% for a wide range of E0. This means that the rotary motor can simultaneously achieve both high efficiency and high power output, which is evident from the closeness of the peak positions for Ẇ and Λ shown in Fig. 4A&B. Indeed, the value of Eg/E0 ≈ 0.29 estimated from experimental data [36], marked by the red arrowed line in Fig. 4A&B, is close to the optimal Eg/E0 ratios for maximum power (blue dot) and maximum efficiency (black star).
Both power and efficiency depend non-monotonically on the energy gap Eg, as shown in Fig. 4A&B. On one hand, a large energy gap can suppress backward steps since k−(θ) = k+(θ + θ0)e−Eg. On the other hand, since the system gains a potential energy ΔV ≡ V (θ) − V (θ − θ0) = G0 − Eg, which converts to mechanical work during the subsequent power stroke, a larger Eg means a smaller work performed by the forward steps. This tradeoff leads to the non-monotonic dependence on Eg and an optimal motor performance (power and efficiency) at a positive finite Eg.
We have determined the maximum efficiency Λ* at different E0 for different κ and ε numerically. Remarkably, as shown in Fig. 5A, the maximum efficiency Λ*, though less than 1, can reach a high value even when most of the back steps are spontaneous, i.e., when κ is small (e.g., 0.1). In fact, Λ* can approach 1 as E0 → ∞ and the difference (1 − Λ*) is found to scale with E0 as ln(E0)/E0 (to the leading order) for E0 ≫1:
| (13) |
where Ce is a prefactor that only depends on κ and ε. Note that energy is expressed in unit of kBT, and E0 should be understood as E0/kBT in the above expression.
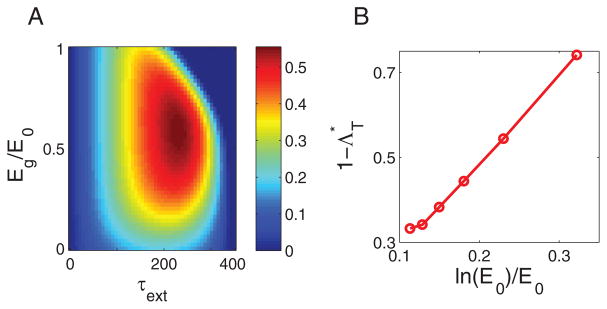
FIG. 5.
Maximum efficiency and optimal design of the motor. (A) The scaling relationship, 1 − Λ* ~ ln(E0)/E0, holds for different values of ε and κ < 1. (B) The optimal energy gap E*g for achieving the maximum efficiency shown in (A). (C) The prefactor Ce in the scaling relation, Eq. (13), decreases with increasing κ for different values of ε. (D) 1 − Λ* versus ln(E0)/E0 for randomly chosen motor designs. Each point corresponds to a random stepping rate profile (see Appendix B for details) with ε = 0.5 and κ = 0.5. All points lie above the envelop line of 1 − Λ* ~ ln(E0)/E0.
Intuitively, the optimal efficiency Λ* is reached by balancing two opposing effects of Eg as mentioned before. A naive design of V (θ) would be to have a large positive torque τ+ given by the driving energy and the step size, τ+ = G0/θ0. However, this naive design would lead to Eg = 0 and thus a high value of k−, which lowers the motor efficiency when κ < 1. Given that k−/k+ = e−Eg depends exponentially on Eg (Eq. (3)), the maximum efficiency shown in Fig. 5A is achieved with the choice of a small but positive energy gap that depends (roughly) logarithmically on E0 as shown in Fig. 5B, which is the origin of the logarithmic dependence in Eq. (13). The prefactor Ce in Eq. (13) is an order 1 constant and decreases weakly with κ for κ ≤ 0.95 as shown in Fig. 5C. It decreases sharply only near κ = 1, but remains finite even at κ = 1 due to the limit on τm discussed before. Ce goes to zero only at the doubly unrealistic case of having both ε = 1 and κ = 1.
To verify the robustness of the maximum efficiency result (Eq.(13)), we performed an extensive search in the motor design space. In particular, we randomly selected the three parameters {kg, ka, kb} for k+(θ) with log10 kg ∈ [0, 4], log10 ka ∈ [0, 3], and log10 kb ∈ [0, 2] uniformly sampled. For a given k+(θ) profile, we determined the maximum efficiency for different choices of V (θ) by varying Eg. In Fig. 5D, each point represents the maximum efficiency for a random E0 ∈ [1, 50]kBT for a random k+(θ) function. As evident from Fig. 5D, a limiting envelope (the dotted line) emerges with the highest efficiency Λ* following the same dependence on E0 as given in Eq. (13): 1 − Λ* ∝ ln(E0)/E0 for large E0 ≫ 1.
2. Efficiency in the presence of external forcing
For most of our study here, we set the external applied torque (force) τext = 0 and change the load by varying ξ. The power of the motor, Ẇ = τ̄ × ω̄, is used to overcome the viscous drag force of the load and the efficiency defined by using this power defintion is called the Stokes efficiency by Wang and Oster [52]. For τext ≠ 0, the output power delivered to overcome this fixed extenal torque is Ẇe ≡ τext ω̄, the effciency based on Ẇe is the so called “thermodynamic” efficiency [5, 53]. Both the thermodynamic efficiency and the Stokes efficiency are well defined in the sense that they are both less or equal than 1. However, in most biological systems there is no active component exerting a fixed force (or torque) on the molecular motor. Instead, a motor needs to overcome a passive drag force from the attached cargoes (loads) in the highly viscose cellular environment with low Reynolds number. Nonetheless, our model can be used to study the thermodynamic efficiency ΛT (κ) ≡ Ẇe/D(κ) with Ẇe ≡ τext ω̄ by varying τext while fixing ξ to be a small value (we take ξ = 0.1 here). As shown in Figure 6, the peak efficiency occurs at an intermediate τext and with a finite gap Eg in the potential to prevent wasteful back steps (Fig. 6A). The dependence of the maximum thermodynamic efficiency on the driving energy E0 (Fig. 6B) also follows the same general trend as for the Stokes efficiency (Fig. 4D and Fig. 5C).
FIG. 6.
The thermodynamic efficiency ΛT and its limit. (A) The dependence of ΛT on the energy gap Eg and the external torque τext. The load ξ = 0.1 is fixed. Other parameters are the same as those in Fig. 4. The optimal ΛT occurs at a finite Eg and an intermediate τext. (B) The optimal depends on the driving energy E0 approximately following the same relation given in Eq. (13) as the optimal Stokes efficiency.
IV. DISCUSSION AND CONCLUSION
In this paper, we search for general principles of designing key microscopic motor properties, specifically the interaction potential V (θ) and the stepping rate function k+(θ), in order to optimize the macroscopic motor performance characterized by its power output and efficiency. Different from previous work, we have taken into account realistic biophysical and biochemical constraints on the shape of V and the reversibility of the mechanochemical cycles (ε < 1, κ < 1) in our investigation. We have studied the detailed dynamics and energetics of the high-performing bacterial flagellar motor in comparison with quantitative experimental data in order to test our general theory, which should be applicable to other molecular motors as well. In the following, we discuss our main general findings and their applications to the BFM together with related work from other groups:
A motor’s power output depends on its torque(or force)-speed dependence. According to our theoretical analysis and simulations, a gating mechanism that allows the ion-assisted stator conformation to occur in a narrow window of relative positions between the stator and the rotor can lead to the observed concave torque-speed curve in CCW BFM. The concavity of the torque-speed curve increases with the gating strength. As a result, the maximum power output, which occurs at an intermediate load level near the knee of the torque-speed curve, increases with the gating strength. In general, a strong gating regime is a key design feature for k+(θ) in order to generate maximum power in a wide range of physiologically relevant loads. Our results also provide a plausible explanation for the almost linear torque-speed curve for the CW state [23]: the gating strength may be weaker in the CW state. The molecular mechanism for gating is unclear, it requires more structural and biochemical studies of the rotor-stator interaction and its effect on regulating ion translocation.
-
The conventional definition of motor efficiency (Λ0) [52] implicitly assumes tight-coupling, i.e., all backward steps regain chemical energy by pumping out ions in the case of BFM or synthesizing ATP in the case of linear motors. In reality, there may be only a fraction κ < 1 of back steps that regain energy. In the case of the linear motor kinesin, experiments show that ATP hydrolysis rate is finite even at stall when there are equal number of forward and backward steps and some backward steps can even cost energy [48, 49]. Here, we show that efficiency peaks at a finite speed and the maximum efficiency is less than 1 as long as there is a finite spontaneous stepping probability, i.e., κ < 1.
In a recent paper[31], Boschert et al. proposed a loose coupling model to explain the less-than-two ions translocation per step in the bacterial flagella motor observed in [36]. The model was based purely on the conformational changes of the stator without considering the motor’s actual physical rotation. It was assumed that the motor can generate a constant torque (or perform work) with either one or two ions bound, but the work done is the same regardless of whether one or two ions passes the membrane. The case of torque generation by two ion translocations can be considered as two forward steps followed by a “wasteful” back step. The assumed finite probability of a power stroke by the stator with two ions bound is consistent with an effective κ < 1 in our model.
The existence of back steps in BFM is strongly suggested [30] by the observed continuity of torque when motors are forced to rotate with a small negative speed [54]. Otherwise, the motor would show a barrier in its torque-speed curve near stall, which was not observed. However, it is not clear whether all back steps pump out ions. We suspect the spontaneous back steps are not negligible, i.e., κ < 1. Future experiments that directly measure ion translocation, specially during forced slow back rotations [54], are needed to test this hypothesis.
We have derived two thermodynamics laws for the nonequilibrium motor. By using these laws for BFM, we showed that the maximum torque at stall should be strictly less than G0/θ0 for any biologically realistic form of V (θ), including the electrosteric potential proposed recently by Mandadapu et al. [32]. The difference G0/θ0 − τmax ≈ στ/τmax is mostly due to torque and speed fluctuations at high loads.
In general, the design of the interaction potential V to optimize the maximum torque (force) and the motor efficiency is dictated by the tradeoff of two opposing effects of the energy gap Eg. For a given energy budget G0 = ΔV +Eg, a steep V (θ) leads to a large ΔV, which increases torque, but at the same time a finite positive Eg is also needed to suppress backward steps, which have the adverse effects of slowing down the motor and wasting energy. As a result of this tradeoff, we obtain a general limit for the optimal efficiency Λ*: 1 − Λ* ∝ ln(E0)/E0. A high efficiency (Eq. (13)) can be achieved at the choice of an optimum energy gap that depends logarithmically on E0 for large E0.
Our model can naturally explain the recent experiments [36] reporting τmax being around 0.71E0/θ0. From our study, this experimental observation indicates an energy gap Eg/E0 ≈ 0.29, which is close to the optimal values of Eg resulting from maximizing the power or the efficiency (see Fig. 4A&B). It remains an interesting open question as to whether the motor has evolved to optimize its performance measured by power output, efficiency, or a combination of the two under physiological constraints. The gerenal model framework should be useful in understanding energetics of other molecular motors. Our results here may also provide guidance in designing more efficient and powerful synthetic motors [55].
Acknowledgments
We thank Dr. B. Hu for discussions in early stage of the work. We aslo thank Dr. C-J Lo for sharing data from [36] and Drs. Howard Berg and Joe Howard for useful discussions. This work is supported by the National Institutes of Health Grant GM081747 (YT).
Appendix A: Detailed derivation of the Fokker-Planck equation for the minimal motor model
There are two processes in motor dynamics, a continuous noisy mechanical motion and discrete stochastic chemical transitions, which can be described by a Langevin equation and the chemical transition rates, respectively: – that can be described by can be described by
| (A1) |
| (A2) |
where η represents the white thermal noise: < η(t)η(t′) >= 2ξkBTδ(t − t′) (kBT is the thermal energy set to 1) and Δθ = θ0 is the step size of chemical transitions. A stator stepping event results in a shift of the interaction potential in the direction of the motor rotation by an angle θ0 and the subsequent motor motion is governed by this new potential until the next stepping event occurs. The stepping rates have a periodicity of 2θ0, i.e., k±(θ) = k±(θ + 2θ0). For physical motion Eq. (A1), we have assumed for simplicity that the rotor and the external load move in unison and denoted their total drag coefficient by ξ. .
Although only two energy landscapes are plotted in Fig. 1A in the main text, the model contains 52 such landscapes. By symmetry and periodicity, once the motor steps forward to the third landscape (which is not shown), the process effectively repeats itself as starting from the first landscape (shown in Fig. 1A). Therefore, this model is equivalent to a particle moving along only two energy landscapes, V1(θ) and V2(θ), which have the same shape and only differ by a half-period shift: V1(θ) = V (θ), V2(θ) = V (θ + θ0).
The system can be described by two coupled Fokker-Planck equations governing the probabilities, P1(θ, t) and P2(θ, t), of the particle in each of the two energy landscapes:
| (A3) |
| (A4) |
where the net flux due to jumping transitions between V1 and V2 is given by Δjs(θ), which can be expressed as:
| (A5) |
where k12(θ) represents the transition rate from the first energy landscape V1, called state 1, to the second landscape V2 downshifted by the effective driving energy G0 (state 2) and k21(θ) is the corresponding reverse transition rate. Included in Δjs are also transitions between V1 and the previous V2 energy landscape shifted up by G0 (called state 2′), as illustrated in Fig. 7. Due to symmetry between the two states (1 and 2), the transition rates between state 2′ and state 1 are the same as those between state 1 and state 2, only shifted by θ0:
as shown in Fig. 7. All these stepping transitions are included in the expression for Δjs above.
All these functions, including V, P1, P2, k12, and k21, are periodic functions with the full period 2θ0. By symmetry, we also have P1(θ) = P2(θ + θ0). Using these relationships and defining P1(θ, t) ≡ P(θ, t), we have P2(θ, t) = P(θ + θ0, t), and the two coupled Fokker-Planck equations, Eq.(A3–A4), can be combined into one equation for P(θ, t) given as Eq. (1) in the main text. For convenience of formulating a single Fokker-Planck equation, we use k± instead of k12 and k21: k12(θ) ≡ k+(θ), k21(θ) ≡ k−(θ − θ0).
A good design of k+(θ) is to allow energy-assisted forward steps to occur only in the half-period region [θ0, 2θ0) so that the stator can “jump” onto the next energy landscape to continue generating positive torque. Therefore, it is favorable to have nonzero k+(θ) ≠ 0 only for θ ∈ [θ0, 2θ0). In this paper, we assume k+(θ) = 0 for θ ∈ [0, θ0). Correspondingly, Eq. (3) requires that k−(θ) = 0 for θ ∈ [θ0, 2θ0). Therefore, we can express k12 and k21 in terms of k±:
| (A6) |
| (A7) |
By plugging the above expressions for k12 and k21 into Eq. (A5), we have the expression for Δjs(θ) as shown in Eq. (4) in the main text.
Appendix B: Details of the model and parameters
An energy barrier VB near the peak of V (θ) is added to prevent slipping between two adjacent FliG’s without stepping. A linear form is used: VB(θ) = H(θB − θ)/θB for θ ∈ [0, θB]; VB(θ) = H(θ − θ0 +θB)/θB for θ ∈ [2θ0 − θB, 2θ0); 0, otherwise. The barrier height is H ≫ kBT, and its width is θB ≪ θ0.
The standard parameters used in this paper are based on previous modeling studies and by fitting our model to available experimental data: θ0 = π/26, θB = 0.005θ0, θg = 0.05θ0, ka = 0, kb = 1 × 104s−1, kg = 5 × 105s−1, H = 50kBT, ξ = 10−3 − 103(pN · nm · rad−1 · s), E0 = 10kBT, ε ∈ (0, 1), κ ∈ (0, 1], kBT = 4.11(pN · nm) for room temperature. Unless specifically mentioned, we used ε = 0.5 and κ = 0.5 in the main text. The units of the parameters are omitted in the main text of the paper, they are the same as given here.
Appendix C: The dependence of Ps(θ) on Eg
The steady state distribution Ps(θ) depends on the energy gap Eg = G0 − Vd/(1 + ε) = G0 − τ+θ0. As explained in the main text and shown in Fig. 8, when Eg decreases the probability in the negative torque regime increases and thus the probability in the positive torque regime P+ = 1 − P− decreases. Together with the fact that τ+ increases with a decreasing Eg, this explains the peak in the maximum torque τm seen in Fig. 3A.
Appendix D: Results with quadratic V (θ)
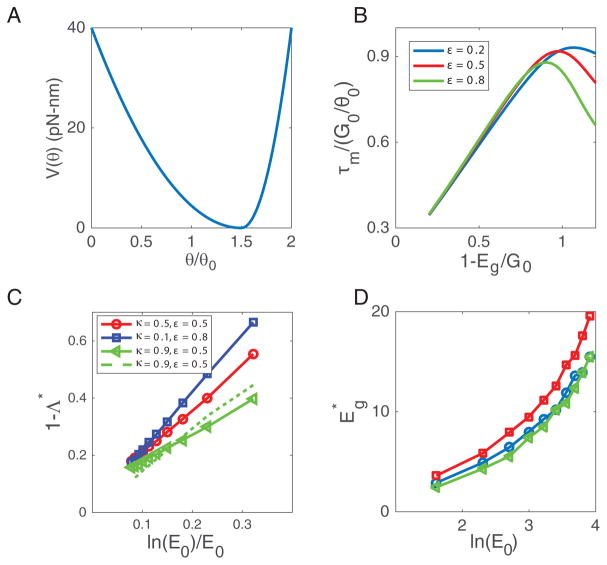
Besides the V-shaped piecewise linear form of V (θ) used in the main text, we have also used other form of V (θ), such as the quadratic form given as:
| (D1) |
which is shown in Fig. 9A. The overall shape of the quadratic potential is given by its depth Vd and it off-centered minimum location (1 + ε)θ0. For such a quadratic potential we repeated what we did in the main text with the energy gap defined as: Eg = G0 − Vd(1 + 2ε)/(1 + ε)2. The results on the maximum torque versus 1−Eg/G0, the maximum efficiency versus ln(E0)/E0, and the optimal versus ln E0 are shown in Fig. 9B&C&D, respectively, which are similar to the results shown in the main text with the piece-wise linear potential.
FIG. 9.
The results for quadratic potentials. (A) The shape of a quadratic potential, expression given in Eq. (D1), in which the minimum location at θm = (1+ε)θ0 and the depth of the potential Vd are varied to optimize motor performance. (B) The maximum torque versus 1 − Eg/G0 = Vd(1+2ε)/[G0(1+ε)2]. (C) 1−Λ* versus ln(E0)/E0, where Λ* is the maximum efficiency. (D) The optimal (for achieving the maximum efficiency) versus ln E0.
References
- 1.Berg HC, Anderson RA. Bacteria swim by rotating their flagellar filaments. Nature. 1973;245:380–382. doi: 10.1038/245380a0. [DOI] [PubMed] [Google Scholar]
- 2.Larsen Steven H, Adler Julius, Jay Gargus J, Hogg Robert W. Chemomechanical coupling without atp: the source of energy for motility and chemotaxis in bacteria. Proc Natl Acad Sci USA. 1974;71:1239–1243. doi: 10.1073/pnas.71.4.1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hirota Norifumi, Kitada Makio, Imae Yasuo. Flagellar motors of alkalophilic bacillus are powered by an electrochemical potential gradient of na+ FEBS Lett. 1981;132:278–280. [Google Scholar]
- 4.Berg HC. The rotatory motor of bacterial flagella. Annu Rev Biochem. 2003;72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- 5.Parmeggiani Andrea, Julicher Frank, Ajdari Armand, Prost Jacques. Energy transduction of isothermal ratchets: Generic aspects and specific examples close to and far from equilibrium. Phys Rev E. 1999;60:2127. doi: 10.1103/physreve.60.2127. [DOI] [PubMed] [Google Scholar]
- 6.Parrondo JMR, de Cisneros BJ. Energetics of brownian motors: a review. Applied Physics A. 2002;75:179–191. [Google Scholar]
- 7.Astumian RD. Thermodynamics and kinetics of molecular motors. Biophysical Journal. 2010;98:2401–2409. doi: 10.1016/j.bpj.2010.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Morimoto YV, Minamino T. Structure and function of the bi-directional bacterial flagellar motor. Biomolecules. 2014;4:217–234. doi: 10.3390/biom4010217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Baker Matthew AB, Hynson Robert MG, Ganuelas Lorraine A, Mohammadi Nasim Shah, Liew Chu Wai, Rey Anthony A, Duff Anthony P, Whitten Andrew E, Jeffries Cy M, Delalez Nicolas J, Morimoto Yusuke V, Stock Daniela, Armitage Judith P, Turberfield Andrew J, Namba Keiichi, Berry Richard M, Lee Lawrence K. Domain-swap polymerization drives the self-assembly of the bacterial flagellar motor. Nat Struct Mol Biol. 2016;23:197–203. doi: 10.1038/nsmb.3172. [DOI] [PubMed] [Google Scholar]
- 10.Asai Yukako, Kojima Seiji, Kato Haruki, Nishioka Noriko, Kawagishi Ikuro, Homma Michio. Putative channel components for the fast-rotating sodium-driven flagellar motor of a marine bacterium. J bacteriol. 1997;179:5104–5110. doi: 10.1128/jb.179.16.5104-5110.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blair David F, Berg Howard C. The mota protein of e. coli is a proton-conducting component of the flagellar motor. Cell. 1990;60:439–449. doi: 10.1016/0092-8674(90)90595-6. [DOI] [PubMed] [Google Scholar]
- 12.Sato Ken, Homma Michio. Functional reconstitution of the na+-driven polar flagellar motor component of vibrio alginolyticus. J Biol Chem. 2000;275:5718–5722. doi: 10.1074/jbc.275.8.5718. [DOI] [PubMed] [Google Scholar]
- 13.Kojima Seiji, Blair David F. Solubilization and purification of the mota/motb complex of escherichia coli. Biochemistry. 2004;43:26–34. doi: 10.1021/bi035405l. [DOI] [PubMed] [Google Scholar]
- 14.Yorimitsu Tomohiro, Kojima Masaru, Yakushi Toshiharu, Homma Michio. Multimeric structure of the poma/pomb channel complex in the na+-driven flagellar motor of vibrio alginolyticus. J biochem. 2004;135:43–51. doi: 10.1093/jb/mvh005. [DOI] [PubMed] [Google Scholar]
- 15.Chun Sang Yearn, Parkinson John S. Bacterial motility: membrane topology of the escherichia coli motb protein. Science. 1988;239:276–278. doi: 10.1126/science.2447650. [DOI] [PubMed] [Google Scholar]
- 16.Roujeinikova Anna. Crystal structure of the cell wall anchor domain of motb, a stator component of the bacterial flagellar motor: implications for peptidoglycan recognition. Proc Natl Acad Sci USA. 2008;105:10348–10353. doi: 10.1073/pnas.0803039105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Block Steven M, Berg Howard C. Successive incorporation of force-generating units in the bacterial rotary motor. Nature. 1984;309:470–472. doi: 10.1038/309470a0. [DOI] [PubMed] [Google Scholar]
- 18.Blair David F, Berg Howard C. Restoration of torque in defective flagellar motors. Science. 1988;242:1678–1681. doi: 10.1126/science.2849208. [DOI] [PubMed] [Google Scholar]
- 19.Manson Michael D, Tedesco PM, Berg Howard C. Energetics of flagellar rotation in bacteria. J mol biol. 1980;138:541–561. doi: 10.1016/s0022-2836(80)80017-9. [DOI] [PubMed] [Google Scholar]
- 20.Khan Shahid, Berg Howard C. Isotope and thermal effects in chemiosmotic coupling to the flagellar motor of streptococcus. Cell. 1983;32:913–919. doi: 10.1016/0092-8674(83)90076-4. [DOI] [PubMed] [Google Scholar]
- 21.Lowe Graeme, Meister Markus, Berg Howard C. Rapid rotation of flagellar bundles in swimming bacteria. Nature. 1987;325:637–1041. [Google Scholar]
- 22.Chen Xiaobing, Berg Howard C. Torque-speed relationship of the flagellar rotary motor of escherichia coli. Biophys J. 2000;78:1036–1041. doi: 10.1016/S0006-3495(00)76662-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yuan Junhua, Fahrner Karen A, Turner Linda, Berg Howard C. Asymmetry in the clockwise and counterclockwise rotation of the bacterial flagellar motor. Proceedings of the National Academy of Sciences. 2010;107:12846–12849. doi: 10.1073/pnas.1007333107. http://www.pnas.org/content/107/29/12846.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Läuger P. Torque and rotation rate of the bacterial flagellar motor. Biophys J. 1988;53:53–65. doi: 10.1016/S0006-3495(88)83065-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Berry Richard M. Torque and switching in the bacterial flagellar motor. an electrostatic model. Biophys J. 1993;64:961. doi: 10.1016/S0006-3495(93)81462-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xing Jianhua, Bai Fan, Berry Richard, Oster George. Torque–speed relationship of the bacterial flagellar motor. Proc Natl Acad Sci USA. 2006;103:1260–1265. doi: 10.1073/pnas.0507959103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mora Thierry, Yu Howard, Sowa Yoshiyuki, Wingreen Ned S. Steps in the bacterial flagellar motor. PLOS Comput Biol. 2009;5:e1000540. doi: 10.1371/journal.pcbi.1000540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Meacci Giovanni, Tu Yuhai. Dynamics of the bacterial flagellar motor with multiple stators. Proc Natl Acad Sci USA. 2009;106:3746–3751. doi: 10.1073/pnas.0809929106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.van Albada Siebe B, Tănase-Nicola Sorin, ten Wolde Pieter Rein. The switching dynamics of the bacterial flagellar motor. Mol Sys Biol. 2009;5 doi: 10.1038/msb.2009.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Meacci Giovanni, Lan Ganhui, Tu Yuhai. Dynamics of the bacterial flagellar motor: The effects of stator compliance, back steps, temperature, and rotational asymmetry. Biophysical Journal. 2011;100:1986–1995. doi: 10.1016/j.bpj.2011.02.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Boschert Ryan, Adler Frederick R, Blair David F. Loose coupling in the bacterial flagellar motor. Proceedings of the National Academy of Sciences. 2015;112:4755–4760. doi: 10.1073/pnas.1419955112. http://www.pnas.org/content/112/15/4755.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mandadapu Kranthi K, Nirody Jasmine A, Berry Richard M, Oster George. Mechanics of torque generation in the bacterial flagellar motor. Proceedings of the National Academy of Sciences. 2015;112:E4381–E4389. doi: 10.1073/pnas.1501734112. http://www.pnas.org/content/112/32/E4381.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Meister Markus, Lowe Graeme, Berg Howard C. The proton flux through the bacterial flagellar motor. Cell. 1987;49:643–650. doi: 10.1016/0092-8674(87)90540-x. [DOI] [PubMed] [Google Scholar]
- 34.Nakamura Shuichi, Kami-ike Nobunori, Yokota Junichi P, Minamino Tohru, Namba Keiichi. Evidence for symmetry in the elementary process of bidirectional torque generation by the bacterial flagellar motor. Proc Natl Acad Sci USA. 2010;107:17616–17620. doi: 10.1073/pnas.1007448107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Meister Markus, Roy Caplan S, Berg HC. Dynamics of a tightly coupled mechanism for flagellar rotation. bacterial motility, chemiosmotic coupling, protonmotive force. Biophys J. 1989;55:905. doi: 10.1016/S0006-3495(89)82889-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lo Chien-Jung, Sowa Yoshiyuki, Pilizota Teuta, Berry Richard M. Mechanism and kinetics of a sodium-driven bacterial flagellar motor. Proc Natl Acad Sci USA. 2013;110:E2544–E2551. doi: 10.1073/pnas.1301664110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sowa Yoshiyuki, Rowe Alexander D, Leake Mark C, Yakushi Toshiharu, Homma Michio, Ishijima Akihiko, Berry Richard M. Direct observation of steps in rotation of the bacterial flagellar motor. Nature. 2005;437:916–919. doi: 10.1038/nature04003. [DOI] [PubMed] [Google Scholar]
- 38.Francis Noreen R, Irikura Vera M, Yamaguchi Shigeru, DeRosier David J, Macnab Robert M. Localization of the salmonella typhimurium flagellar switch protein flig to the cytoplasmic m-ring face of the basal body. Proc Natl Acad Sci USA. 1992;89:6304–6308. doi: 10.1073/pnas.89.14.6304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Thomas Dennis R, Francis Noreen R, Xu Chen, DeRosier David J. The three-dimensional structure of the flagellar rotor from a clockwise-locked mutant of salmonella enterica serovar typhimurium. J bacteriol. 2006;188:7039–7048. doi: 10.1128/JB.00552-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Feynman RP, Leighton RB, Sands M. The Feynman Lectures on Physics. I. Addison-Wesley; Reading, MA: 1966. [Google Scholar]
- 41.Parrondo Juan MR, Blanco JM, Cao Francisco, Brito R. Efficiency of brownian motors. EPL (Europhysics Letters) 1998;43:248–254. [Google Scholar]
- 42.Golubeva N, Imparato A, Peliti L. Efficiency of molecular machines with continuous phase space. EPL (Europhysics Letters) 2012;97:60005. [Google Scholar]
- 43.Jülicher Frank, Ajdari Armand, Prost Jacques. Modeling molecular motors. Rev Mod Phys. 1997;69:1269–1282. [Google Scholar]
- 44.Schmiedl T, Seifert U. Efficiency of molecular motors at maximum power. EPL (Europhysics Letters) 2008;83:30005. [Google Scholar]
- 45.Esposito Massimiliano, Lindenberg Katja, Van den Broeck Christian. Universality of efficiency at maximum power. Phys Rev Lett. 2009;102:130602. doi: 10.1103/PhysRevLett.102.130602. [DOI] [PubMed] [Google Scholar]
- 46.Svoboda Karel, Schmidt Christoph F, Schnapp Bruce J, Block Steven M. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 1993;365:721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- 47.Bowater R, Sleep J. Demembranated muscle fibers catalyze a more rapid exchange between phosphate and adenosine triphosphate than actomyosin subfragment 1. Biochemistry. 1988;27:5314–5323. doi: 10.1021/bi00414a055. [DOI] [PubMed] [Google Scholar]
- 48.Carter NJ, Cross RA. Mechaniscs of the kinesin step. Nature. 2005;435:308. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 49.Liepelt Steffen, Lipowsky Reinhard. Kinesin’s network of chemomechanical motor cycles. Phys Rev Lett. 2007;98:258102. doi: 10.1103/PhysRevLett.98.258102. [DOI] [PubMed] [Google Scholar]
- 50.Blair DF, Berg HC. Mutations in the mota protein of escherichia coli reveal domains critical for proton conduction. J Mol Biol. 1991;221:1433–1442. doi: 10.1016/0022-2836(91)90943-z. [DOI] [PubMed] [Google Scholar]
- 51.Braun TF, Poulson S, Gully JB, Empey JC, Van Way S, Putnam A, Blair DF. Function of proline residues of mota in torque generation by the flagellar motor of escherichia coli. Journal of Bacteriology. 1999;181:3542–3551. doi: 10.1128/jb.181.11.3542-3551.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wang Hongyun, Oster G. The stokes efficiency for molecular motors and its applications. EPL (Europhysics Letters) 2002;57:134. [Google Scholar]
- 53.Zimmermann Eva, Seifert Udo. Efficiencies of a molecular motor: a generic hydrib model applied to the f1-atpase. New Journal of Physics. 2012;14:103023. [Google Scholar]
- 54.Berry Richard M, Berg Howard C. Absence of a barrier to backwards rotation of the bacterial flagellar motor demonstrated with optical? tweezers. Proceedings of the National Academy of Sciences. 1997;94:14433–14437. doi: 10.1073/pnas.94.26.14433. http://www.pnas.org/content/94/26/14433.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cheng C, McGonigal PR, Stoddart JF, Astumian RD. Design and synthesis of nonequilibrium systems. ACS Nano. 2015;9:8672–8688. doi: 10.1021/acsnano.5b03809. [DOI] [PubMed] [Google Scholar]