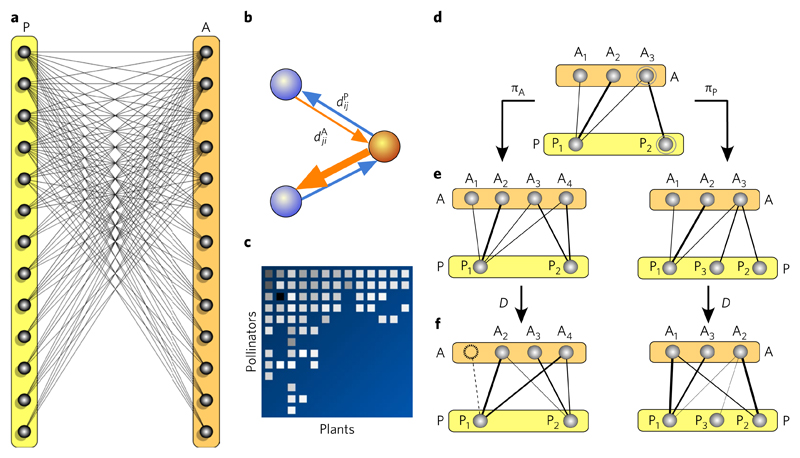
Fig. 1. Mutualistic webs and how to model their evolution.
a, Mutualistic networks are bipartite graphs involving two types of interacting species, such as plants (P) and animals (A). Each link in the graph indicates the existence of an ecological link, such as a frugivore–plant interaction. b, For each pairwise interaction between species i and j, we can obtain two values of mutual dependency: for the dependence of the animal species j on plant species i (orange arrow), and for the dependence of plant species i on animal species j (blue arrow). The arrows point to the intrinsic direction of the corresponding dependence. If the strength of this interaction is known, the resulting web is weighted. In this case, directional connections need to be considered. The strength might be estimated, for example, by the number of encounters among the members of the pair over a given time window. c, The structure of the interaction matrix resulting from this bipartite graph can be arranged in such a way that node labels are assigned in descending order of degree. d, A simple evolutionary model can be defined by means of a set of duplication-divergence rules. Here, the graph starts with SA = 3 (upper) and SP = 2 (lower) species, respectively. Speciation can affect either the A or the P sets with probabilities πA and πP, respectively. e, Each time a new species is added, the daughter species inherits all its interactions. f, Afterwards, the network experiences a divergence (D) affecting the weights and links.