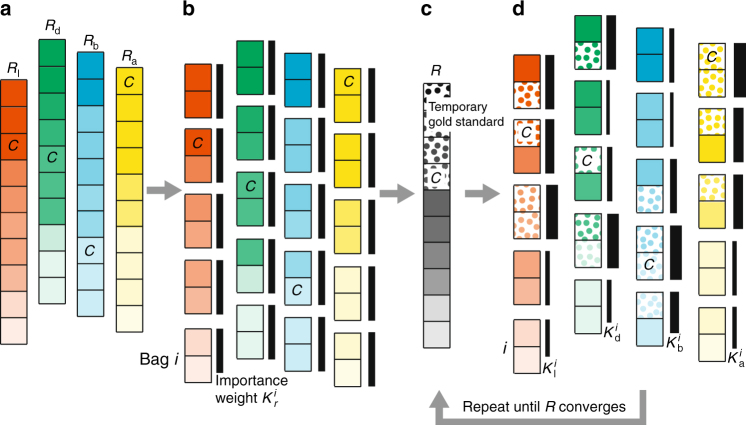
Fig. 5.

Combining community prioritization metrics without an external gold standard. a The rank aggregation algorithm starts with four ranked lists of communities, R_r, each one arising from the values of a different community prioritization metric r (where r is one of “l”— likelihood, “d”—density, “b”—boundary, “a”—allegiance). Communities are ordered by the decreasing value of the metric. We use C to indicate the rank of an illustrative community by the community prioritization metrics and at different stages of the algorithm. b Each ranked list is partitioned into equally sized groups, called bags. Each bag i in ranked list R_r has attached importance weight $K_r^i$ whose initial values are all equal (represented by black bars all of same width). CRank uses the importance weights $K_r^i$ to initialize aggregate prioritization R as a weighted average of community ranks R_l, R_d, R_b, R_a. c The top-ranked communities (denoted as dotted cells) in the aggregated prioritization R serve as a temporary gold standard, which is then used to iteratively update the importance weights $K_r^i$. d In each iteration, CRank updates importance weights using the Bayes factor calculation³⁶ (Supplementary Note 4). Given bag i and ranked list R_r, CRank updates importance weight $K_r^i$, based on how many communities from the temporary gold standard appear in bag i. Updated importance weights then revise the aggregated prioritization in which the new rank R(C) of community C is expressed as: R(C) = ${\sum }_r\log K_r^{i_r\left(C\right)}{R}_r\left(C\right)$, where $K_r^{i_r\left(C\right)}$ indicates the importance weight of bag i_r(C) of community C for metric r, and R_r(C) is the rank of C according to r. By using an iterative approach, CRank allows for the importance of a metric not to be predetermined and to vary across communities