Etiology of Stability and Growth of Internalizing and Externalizing Behavior Problems Across Childhood and Adolescence

Psychiatric problem behaviors show marked stability, with variation as early as age three years predicting adult psychiatric dysfunction (Caspi, Moffitt, Newman, & Silva, 1996; Hofstra, van der Ende, & Verhurlst, 2000). However, developmental trajectories of problem behaviors (e.g., in latent growth models or LGMs) are also of considerable interest to psychologists, as individual differences in change may be useful for understanding how risk factors influence vulnerability to psychopathology (e.g., Fanti & Henrich, 2010; Keiley, Bates, Dodge, & Pettit, 2000; Lansford et al. 2006; Lee & Bukowski, 2012). Although LGMs are quite popular in the developmental literature, they have been less so within the behavioral genetic literature; thus, there are few studies investigating genetic and environmental etiology of individual differences in problem behavior trajectories. In the current study, we estimate biometrical components for latent growth curves of internalizing and externalizing behaviors across childhood and adolescence.

We used a broad level of analysis for examining problem behaviors. It has been well-characterized that symptoms of different disorders covary (Krueger, 1999). Krueger and Eaton (2015) argued that this covariation is due to underlying behavioral liabilities of internalizing and externalizing behavior, which are thought to reflect broader characteristics fundamental to multiple psychiatric disorders. Internalizing behaviors are characterized by the tendency to withdraw and take in distress (e.g., anxiety and depression), whereas externalizing behaviors are characterized by expelling or acting out distress (e.g, conduct disorder, substance use disorders, and in some cases, attention-deficit/hyperactivity disorder).

The Child Behavior Checklist (CBCL) and Teacher Report Form (TRF; Achenbach, 1991a, Achenbach, 1991b) are well-validated instruments to assess these behavior problems in childhood and adolescence. They include internalizing and externalizing major scales, which are made up of subscales of problem behaviors that cluster into overarching internalizing and externalizing behavior factors (Achenbach, 1991a; 1991b). These scales show concurrent validity with other measures of internalizing and externalizing variability, including tasks of adaptive function, current and later use of mental health services, academic problems, and police contact (Cohen, Gotlieb, Kershner, &Wehrspann, 1985; Verhulst, Koot, & van der Ende, 1994).

A number of studies have explored the development of internalizing and externalizing problems using the CBCL/TRF (Fanti & Henrich, 2010; Keiley et al., 2000; Lansford et al. 2006; Lee & Bukowski, 2012), and some of these have also investigated genetic underpinnings (Haberstick, Schmitz, Young, & Hewitt, 2005; Valk, van den Oord, Verhulst, & Boomsma 2003; Bartels et al. 2004). However, there has been little research exploring how genetic and environmental influences explain individual differences in the extent to which these behaviors increase or decrease across time.

Etiology of Internalizing and Externalizing Behavior Development

There is a wealth of cross-sectional research on the etiology of internalizing and externalizing behavior. Significant genetic and environmental components have been demonstrated across many ages, with heritabilities around 25% to 45% for internalizing and 35% to 65% for externalizing in twins ages 5 to 9 and 12 to 15 years (e.g., Gjone & Stevenson, 1997; see also Towers et al., 2000).

Beyond cross-sectional analysis, there are prior genetic studies on the development of these problem behaviors that are particularly relevant for the current study. Haberstick et al. (2005) estimated longitudinal simplex models of teacher-rated internalizing and externalizing behaviors from ages 7 to 12 years, using a subset of the same twin data used in the current study. They found that for both internalizing and externalizing behavior, stability was due primarily to genetic transmission across age, whereas change was due to age-specific genetic and nonshared environmental influences. In mother-rated data of 3- and 7-year old twins, van der Valk, van den Oord, Verhulst, and Boomsma (2003) also found high stability of genetic effects. With a genetic simplex model of the same sample examined by van der Valk et al., Bartels et al. (2004) found that genetic transmission explained 53% to 67% of externalizing stability (for girls and boys) and 47% of internalizing stability from ages 3 to 12, with most of the remaining stability due to a shared environmental common factor. Change was primarily due to nonshared environmental influences, with some small significant genetic and shared environmental innovations at each time point. Finally, Huizink, van den Berg, van der Ende, and Verhulst (2007) examined parent-rated longitudinal problem behavior for adoptees when they were aged 12, 15, and 26 years. Their final models included common genetic and shared environmental factors accounting for stability, and nonshared environmental influences accounting for change in the externalizing model, and both stability and change in the internalizing model.

Taken together, these prior studies suggest stability in problem behaviors throughout childhood and adolescence is primarily due to shared genetic influences, though stability in parent-rated behavior is also due to shared environmental influences. Change is typically primarily due to nonshared environmental influences, which also include measurement error; in some cases age-specific genetic influences contribute to change as well.

These studies primarily used common factor or simplex models to capture the developmental processes in the longitudinal data. Simplex models estimate the extent to which genetic and environmental influences are transmitted from one time point to the next, and whether there are new genetic and environmental influences at each time point. Such models are useful for understanding the etiology of individual differences and the extent to which rank orders stay the same or change across time. However, neither simplex models nor common factor models capture trajectories of change and the association between change and stability. While mean structures are often estimated in common factor, Cholesky, and simplex models, growth models include latent variables to capture individual differences in intercepts and slopes of trajectories. In the current study, we extend this literature by estimating biometrical components for latent growth curves of internalizing and externalizing behaviors across two raters to elucidate how etiological factors influence developmental trajectories of internalizing and externalizing behavior across childhood and adolescence.

Stability and Growth of Internalizing and Externalizing Behaviors

Latent growth models (LGMs) are often used to study phenotypic patterns of internalizing and externalizing behavior (e.g., Fanti & Henrich, 2010; Keiley et al., 2000; Lansford et al. 2006; Lee & Bukowski, 2012). LGMs typically include at least two random latent factors (see Bollen & Curran, 2006). A latent Intercept factor equally predicts variation in all time points, capturing variability in the first time point that is maintained across development (i.e., stability). A Slope factor is parameterized to measure individual variation in the rate at which behaviors change (increase/decrease) across time. These random factors also have means, with the mean Intercept equal to the average level of the behavior at the first-time point, and the mean Slope equal to the average change. A positive mean for the Slope would indicate that, on average, individuals increase in that behavior across time, and significant Slope variation would indicate significant individual differences in the rate of increase. Finally, a covariance between the Intercept and Slope factors is estimated, which represents the extent to which individual differences in initial levels relate to individual differences in the rate of change across time. For example, a positive covariance between Intercept and Slope would indicate that individuals with high initial levels tend to have larger increases across time.

Past studies using LGMs with these phenotypes have found that there are significant individual differences in stability (Intercepts) and change (Slopes) across time, regardless of sex, for externalizing (e.g., Lee & Bukowski, 2012). With respect to the variation in the Slopes (change) for internalizing, Keiley et al., (2000) did not find significant variance, whereas Lee and Bukowski did.

While many developmental psychopathology researchers have embraced LGMs, behavioral genetics has relied largely on simplex models and Cholesky decompositions to study the development of psychiatric behaviors. In terms of determining whether the same genes are acting across time, both the standard Cholesky decomposition and simplex models have been applied successfully (e.g., Haberstick et al., 2005). A key strength of these commonly applied models is that they estimate whether there are genetic innovations across time. The latent growth model allows for similar tests of the developmental pattern, but is parameterized to characterize (1) overall change across all time points (i.e., the mean of the latent Slope factor), (2) individual differences in change across time (i.e., the variance of the Slope factor), and (3) the association between individual differences in initial levels or stability and change (i.e., the correlation between the Intercept and Slope factors). Thus, decomposing the latent growth factors into genetic and environmental components will reveal how genes and environmental factors influence individual differences in change and its relation to initial levels (see Neale & McArdle, 2000).

Goals of The Current Study

The main questions we address are the following: 1) What is the genetic and environmental etiology of stability and change in internalizing and externalizing behaviors across childhood and adolescence? And 2) How do etiological patterns influence the relationship between stability and change? We predicted that there will be significant genetic effects on the stability factor (Intercept), considering that past literature reviewed earlier has found evidence for genetic common factors or genetic transmission. Additionally, we hypothesized that these genetic effects on the Intercepts would also influence the Slopes, accounting for commonly observed phenotypic correlations between Intercept and Slope in the psychopathology literature (e.g., borderline personality disorder; Bornovalvoa, Hicks, Iacono, & McGue 2009). However, we thought there might also be specific effects of the environment, and perhaps also unique genetic effects, on the Slopes, since no past literature has found a correlation of 1.0 between Intercept and Slope at the phenotypic level.

To answer these questions, we first report the univariate phenotypic growth models for parent-rated and teacher-rated internalizing and externalizing behavior. These analyses are based on our prior work with these models (Hatoum et al., in press), in which we evaluated phenotypic sex differences in these models and determined that models could be constrained across sex. After estimating the phenotypic models, we then estimate biometrical components separately in all four models to explore how additive genetic (A), shared environment (C), and nonshared environment (E) contribute to these traits, and what proportions of A, C, and E are shared between Intercept and Slope.

Method

Participants

Participants were 216 monozygotic (MZ) and 192 DZ twin pairs rated by teachers and 231 (MZ) and 201 (DZ) twin pairs rated by parents. All DZ pairs were same-sex. All twins were recruited as a part of the Colorado Longitudinal Twin Study (LTS; Rhea, Gross, Haberstick, & Corley, 2006, 2013). The LTS is a longitudinal study of emotional and cognitive development of 483 same-sex twin pairs recruited through the Colorado Department of Health from 1984–1990. Twins included in the current analyses were those with ratings from teachers and/or parents at ages 7 to 16 years on internalizing and externalizing behaviors. The years correspond to school grades (e.g., age 7 years corresponded to 2^nd grade). Tables I and II report sample sizes for each rater at each time point¹ . Table I reports the mean and standard deviation of each time point before binning. As these variables were non-normal, Table I means to do not represent the thresholds for the estimated growth models and simply represent summary statistics for the sample. The analyses models the underlying liability distribution at each time point.

Table I.

Descriptive Statistics for Problem Behaviors by Rater and Sex of Child

Year	Age in Years (SD)	Mean Internalizing (SD)	Mean Externalizing (SD)	Full n
Teacher Ratings
Female children
Year 7	7.39 (0.36)	5.27 (5.76)	3.91 (7.11)	289
Year 8	8.38 (0.34)	4.33 (4.78)	3.31 (5.66)	270
Year 9	9.40 (0.38)	4.87 (5.53)	3.97 (7.35)	261
Year10	9.93 (0.38)	4.82 (5.77)	3.20 (5.56)	253
Year 11	11.38 (0.38)	4.04 (4.58)	2.88 (5.67)	249
Year 12	12.40 (0.37)	4.32 (5.11)	2.43 (4.43)	234
Year 13	12.87 (0.44)	4.48 (5.34)	2.27 (5.36)	203
Year 14	13.90 (0.40)	4.12 (4.37)	2.32 (4.37)	188
Year 15a	14.81 (0.40)	3.52 (5.24)	2.37 (4.94)	136
Male children
Year 7	7.50 (0.39)	5.42 (5.89)	7.03 (9.50)	285
Year 8	8.47 (0.37)	6.00 (6.42)	7.18 (9.03)	263
Year 9	9.49 (0.39)	5.47 (6.19)	6.51 (8.58)	248
Year10	9.99 (0.41)	5.53 (5.70)	6.00 (8.21)	258
Year 11	11.41 (0.36)	5.17 (6.28)	6.32 (8.52)	252
Year 12	12.47 (0.38)	4.19 (5.49)	5.23 (8.39)	204
Year 13	12.98 (0.45)	4.70 (5.72)	5.06 (8.15)	172
Year 14	13.97 (0.43)	4.36 (5.79)	5.76 (8.57)	167
Year 15a	14.90 (0.35)	3.93 (5.02)	3.36 (5.40)	120
Parent Ratings
Female children
Year 7	7.43 (0.36)	4.90 (4.50)	6.63 (5.72)	319
Year 9	9.40 (0.38)	5.13 (5.19)	6.43 (6.24)	327
Year10	9.93 (0.38)	4.92 (4.85)	5.78 (5.77)	299
Year 11	11.38 (0.38)	4.39 (4.96)	4.65 (5.13)	234
Year 12	12.40 (0.37)	5.71 (6.12)	5.94 (6.60)	340
Year 13	12.87 (0.44)	4.90 (5.51)	5.23 (6.16)	273
Year 14	13.90 (0.40)	5.34 (6.03)	5.10 (6.86)	260
Year 15a	14.81 (0.40)	4.34 (5.41)	3.80 (4.83)	186
Year 16	16.59 (0.83)	6.10 (6.51)	5.46 (6.82)	322
Male children
Year 7	7.43 (0.36)	4.64 (4.61)	8.75 (7.08)	308
Year 9	9.49 (0.39)	4.92 (5.11)	8.25 (7.07)	311
Year10	9.99 (0.41)	4.85 (4.96)	7.47 (6.81)	279
Year 11	11.41 (0.36)	4.92 (5.32)	7.81 (7.41)	258
Year 12	12.47 (0.38)	5.09 (4.86)	7.59 (6.88)	312
Year 13	12.98 (0.45)	4.85 (5.49)	7.27 (7.39)	233
Year 14	13.97 (0.43)	4.52 (4.85)	6.90 (6.90)	223
Year 15a	14.90 (0.35)	3.89 (5.24)	5.84 (7.02)	165
Year 16	16.57 (0.75)	4.99 (5.68)	7.56 (8.56)	313

Note. Reproduced with permission from Hatoum et al. (in press).

^aFor twins whose 16^th birthdays were within 4 months of when the age 15 assessment would have been completed, the age 15 assessment was skipped, resulting in a smaller n for that year.

Table II.

Sample Size by Zygosity and Time Point

Year	Teacher Ratings		Parent Ratings
	MZ	DZ	MZ	DZ
Year 7	153	137	167	143
Year 8	153	131	--	--
Year 9	142	113	170	147
Year 10	140	114	173	145
Year 11	143	117	174	146
Year 12	134	117	158	134
Year 13	142	107	155	131
Year 14	140	112	124	120
Year 15	117	96	126	122
Year 16	--	--	173	154

Note. Number of twins per time point per rater and zygosity. Ns did not vary between internalizing and externalizing scales within raters. Overall teacher N = 216 MZ and 192 DZ; overall parent N = 231 MZ and 201 DZ.

The LTS is 86.6% Caucasian, 8.5% Hispanic, 1.2% Asian, .7% African American, and 2.9% other. Zygosity was initially determined with a 10-item questionnaire, but was followed up by comparing the identities of nine or more polymorphic simple tandem repeat markers between the twins in 92% of the sample. More specifics about this sample can be found elsewhere, including rules for inclusion/ineligibility (Rhea, et al., 2006, 2013).

Measures

Both the CBCL and TRF are checklists that contain several subscales of problem behaviors. Teachers and parents were asked to rate the child on each item on a scale of 0 = “Not true (as far as you know),” 1 = “Somewhat or sometimes true,” and 2 = “Very true or often true.” The internalizing scale is composed of the anxious-depressed attachment style, somatic complaints, and withdrawn/depressed scales, with a total of 35 items for teachers (highest possible score of 70), and 31 for parents (highest possible score 62). The externalizing scale is composed of the aggressive and delinquent subscales, totaling 34 items for teachers (highest possible score of 68), and 33 for parents (highest possible score 66). These scales show concurrent validity with other measures of internalizing and externalizing behavior problems (Cohen et al., 1985; Verhulst et al., 1994).

Before the yearly spring assessment, surveys were mailed to parents, with instructions to give or mail the TRF to the twins’ teachers. Parent and/or teacher reports were returned yearly (year 8 parent report was skipped) either by mail or during the yearly assessment.

Data Transformation and Analysis

The internalizing and externalizing scales in our sample were not normally distributed. Specifically, they were characterized by a positively skewed distribution, with many scores of zero; thus, standard transformations could not be used to normalize the distributions. To allow for estimation of the structural models, we employed a binning procedure. We chose bins to capture variability while including enough subjects in each bin to avoid empty cells in the bivariate cross-tabs used to compute polychoric correlations; these bins are the same as used in prior studies (Rhee et al. 2013, Hatoum et al. under review). For both internalizing and externalizing measures across all time points, scores were binned as follows: Zero; 1–3; 4–10; and greater than 10. The binned variables were analyzed as ordinal variables in Mplus, which assumes an underlying normal liability distribution by estimating thresholds for the bin transitions. Analyzing non-normal censored data as ordinal (vs. as normal after transformations) has been shown to recover the most accurate estimates from biometrical parameters (Derks, Dolan, & Boomsma, 2004).

All analyses were conducted with Mplus, version 7.4 (Muthen & Muthen, 1998–2014), using WLSMV (Weighted Least Squares Means and Variances adjusted) estimator and the default delta parameterization. The delta parameterization fixes to 1.0 the total variance of the underlying normal liability distributions used to model the observed categories, so residual variances are not free parameters, but are derived as a remainder of 1 minus the variance predicted by the factor(s). Scaling factors are used to capture differences in variances across time. We used the default in Mplus of fixing the scaling factor for the first time point to 1.0, and freeing those for the remaining time points.

The phenotypic analyses used the clustering (type = complex) option, which uses a weighted likelihood function and a sandwich estimator to obtain a scaled chi-square (χ²) and standard errors corrected for the non-independence of twins. Both phenotypic and twin models assessed model fit with the χ² statistic, supplemented with the root-mean-square error of approximation (RMSEA) and the Comparative Fit Index (CFI). We used RMSEA < .06 and CFI > .95 as indications of good fit (Hu & Bentler, 1998). Parameter significance in the phenotypic models was assessed with z-scores formed from dividing the estimate by its standard error; parameter significance in the genetic models were assessed with bootstrapped confidence intervals, where a 95% confidence interval must exclude zero to be significant.

Models

Parameterization of growth factors

We estimated biometrical components for latent growth factors for internalizing and externalizing separately. As in our prior phenotypic work with these models (see Hatoum et al., in press, for more on these models, including sex invariance tests and missingness analysis) we used the latent basis growth model to allow for departures from linearity across time (Bollen & Curran, 2006; Meredith & Tisak, 1990; Ram & Grimm, 2007). Allowing for nonlinearity is appropriate for models of psychiatric behaviors across long periods of time, which are known to show nonlinear patterns (Kazdin & Kagan, 1994; Kim & Cicchetti, 2006).

In the latent basis growth model, unstandardized Intercept loadings were fixed at 1.0 for all time points; and the Slope loading for the first time point was set to 0, the loading for the final time point was set to 1.0, and the remaining loadings were freely estimated. With this parameterization, scores on the Slope factor correspond to mean changes from the first to the last time point, and multiplication of the mean Slope by each loading gives the predicted difference between that time point and the first time point. Each freed loading estimate represents the proportion of change in the phenotype by that time point. For example, if the first estimated loading (i.e., for age 8) is 0.1, that indicates that 10% of the difference from age 7 to age 15 has occurred by the second time point. Thus, a consistent increase in the loadings shows a pattern of steady change, while inconsistently increasing loadings indicate that change follows a nonlinear pattern. Note that the loadings for the intermediate time points can be estimated at less than zero or greater than 1.0, which would indicate that the estimated mean for that time point was lower than that of the initial time point, which has a loading of zero, or higher than the final time point, which has a loading of 1.0. We included sex as a covariate by regressing the growth factors on sex, coded as .5 for males and–.5 for females.

This parameterization of growth is well-suited for this study because it allows for nonlinear patterns of change without additional polynomial (e.g., quadratic and cubic) growth factors, which can be collinear and difficult to interpret in terms of underlying developmental processes (Ram & Grimm, 2007). Thus, the latent basis growth model allows for simple bivariate decomposition of the ACE parameters through standard analysis (e.g., Cholesky decomposition), making it ideal for twin modeling. Additionally, this model allows for the direct observation of the overall pattern of change across the data by interpreting the factor loadings. Additionally, unlike a linear curve, the latent basis model is not nested under the polynomial model, and is a direct nonlinear curve fitting procedure within a structural equation modeling estimation procedure. To our knowledge, this is the first application of this model in a behavioral genetic paradigm.

Growth models on continuous data typically constrain the intercepts of the individual time points to zero to identify the mean of the latent Intercept factor. However, for these ordinal variables analyzed with a liability-threshold model, we followed the typical approach (and the Mplus default) of setting the latent Intercept mean to zero and freely estimated a single set of thresholds, which are constrained to be equal across time. The figures include these estimated thresholds, which correspond to the predicted distribution of the underlying liability at the initial time point.

ACE models

We used a bivariate ACE Cholesky decomposition to partition the variances and covariance of the Intercept and Slope factors. However, in the figures, we present parameter estimates for correlated ACE models, derived from these Cholesky decompositions, as correlated Intercept and Slope growth models are more common in the developmental literature. Because we computed these paths within the Mplus scripts, we were able to estimate their confidence intervals, which are also shown in the figures. Supplementary Figures 1 and 2 present the Cholesky decompositions. To allow residual A or C effects on the time-specific variances (i.e., variability in time points not explained by the growth factors), we allowed time-specific residual correlations across twins to vary across MZ and DZ groups. We constrained thresholds, variances, path estimates, and residual variances (i.e., scaling factors in the delta parameterization) for each time point to be equal across twins, in line with common assumptions for twin models.

Results

Phenotypic Growth Models

We began by estimating the phenotypic LGMs. In prior work (Hatoum et al. 2017), we examined the sex invariance and shape of the curves in these same individuals and measures. Slope loadings could be constrained across sex in both teacher models and the parent externalizing model without significant decrement to fit, all χ² difference (7) < 7.37, p > .391. Although the loadings for the parent internalizing model significantly differed across sex, the difference was not large, χ² difference (7) = 14.82, p = .038. When loadings were constrained, we found that the sexes differed in their means for the latent growth factors, but their factor variances could be equated in all four models. Thus, for sake of consistency and power to detect genetic effects, in the current study we estimated the same phenotypic model for males and females, with sex as a covariate, as shown in Figures 1 and 2.

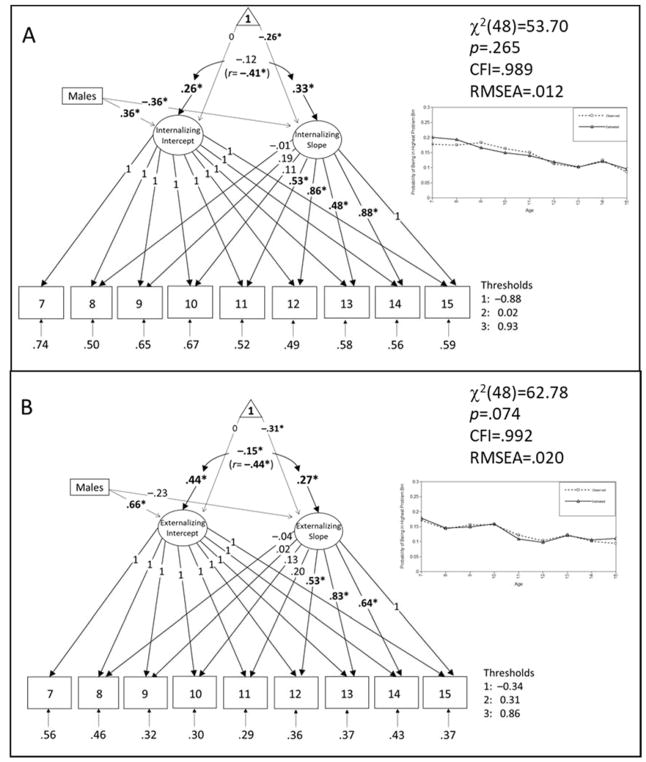
Figure 1.

Teacher-rating phenotypic models for internalizing (panel A) and externalizing (panel B) behaviors. Parameter estimates are unstandardized for thresholds, loadings, means, and residual variances and covariances, but standardized with respect to the growth factors for the paths from sex. These standardized regression betas from sex capture the mean difference across sex (males – females) in standard deviation units. Sex was centered; thus the intercepts shown on the arrows from the triangle are the latent variable grand means. The values in parentheses are the residual correlations for the Intercepts and Slopes. Standardized residual variances for each time point are also shown. Fit statistics and spaghetti plots showing observed and estimated mean curves for probability of the highest category are shown to the right of the path models. *p<.05.

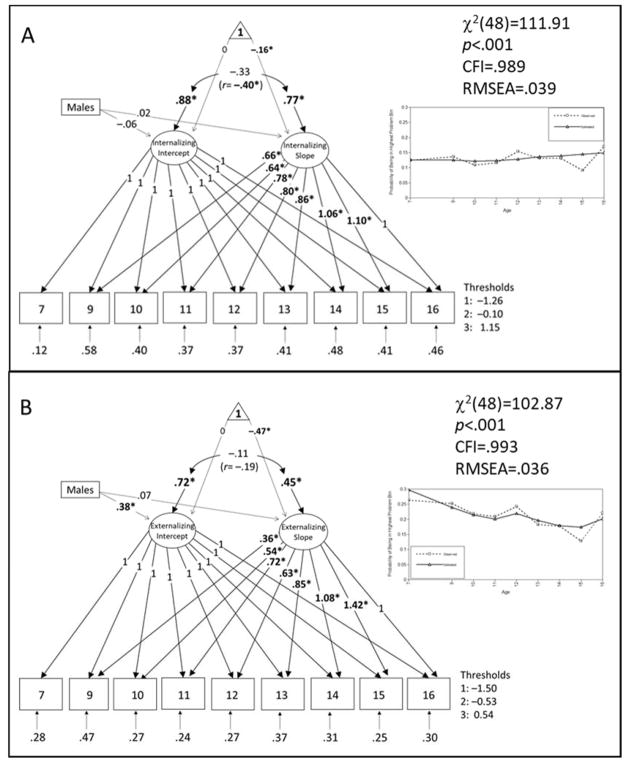
Figure 2.

Parent-rating phenotypic models for internalizing (panel A) and externalizing (panel B) behaviors. Parameter estimates are unstandardized for thresholds, loadings, means, and residual variances and covariances, but standardized with respect to the growth factors for the paths from sex. These standardized regression betas from sex capture the mean difference across sex (males – females) in standard deviation units. Sex was centered; thus the intercepts shown on the arrows from the triangle are the latent variable grand means. The values in parentheses are the residual correlations for the Intercepts and Slopes. Standardized residual variances for each time point are also shown. Fit statistics and spaghetti plots showing observed and estimated mean curves for probability of the highest category are shown to the right of the path models. *p<.05.

The loadings and spaghetti plots in Figures 1 and 2 show some nonlinearity in the curves. In prior work (Hatoum et al. 2017), we compared these models with freed Slope loadings to nested models with linear slopes. Those comparisons confirmed significant non-linearity for both parent-rated internalizing and externalizing behaviors, both χ² difference (7) > 26.00, p < .001, with marginal significance for the teacher-rated externalizing model, χ² difference (7) = 12.28, p =.092, but not the teacher-rated internalizing model, χ² difference (7) = 11.22, p =.129. Again, to maintain consistency across models, we have opted to estimate Slope loadings for all four models; when the observed curves are closer to linear, these loadings will be estimated at values close to those that would be specified for a linear curve.

Due to the regression of the latent factors on sex, the mean of the random factors is represented as an intercept. We centered sex, such that this intercept captures the average of the means for males and females. For example, in the teacher-rated internalizing model, this intercept for the Slope factor is –.26, which means that on average across males and females, internalizing scores decrease from the first to the last time point; specifically, the mean of the underlying liability distribution for age 15 years is .26 standard deviations lower than that for age 7 years (that is, there are fewer individuals in the bins corresponding to higher levels of problems at age 15, compared to the numbers in these bins at age 7). The coefficient for the regression on sex indicates the difference in the standardized latent factor means between sexes (i.e., males minus females). For example, in that same teacher-rated internalizing model, the sex effect of –.36 on the Slope indicates that boys’ Slopes are .36 standard deviation units lower than females’ Slopes, on average. To avoid confusion, we refer to the intercepts of the growth factors as means in the following sections.

Teacher ratings

The internalizing model shown in Figure 1A fit well, χ²(48)=53.70, p=.265, CFI=.989, RMSEA=.012. The unstandardized mean of the Slope was negative and significant (μ= –.26, p<.001). This negative mean suggests that overall, teacher-rated internalizing behaviors decreased from age 7 to 15, consistent with recent findings on internalizing symptomatology (Conway, Zinbarg, Mineka, & Craske, 2017). Unstandardized residual variances of the Intercept (ζ=.26, p<.001) and Slope (ζ=.33, p=.025), after accounting for sex, were significant, and they were negatively correlated (r=–.41, p=.003). Thus, individuals who start with the highest internalizing problems have slower declines in their rate of internalizing.

Examination of the Slope loadings (shown in Table III with their 95% confidence intervals) reveals that at ages 8 to 10, there was nonsignificant change in teacher-rated internalizing scores. By age 11, approximately half (.53) of the total decrease (the negative mean for the Slope factor) from ages 7 to 15 had occurred, and by age 12, .86 of the decrease had occurred. There was a slight increase in scores at age 13, as indicated by the .48 loading, which is smaller than the loadings at the surrounding years.

Table III.

Unstandardized Loadings for Slope Factors in Univariate Phenotypic Model

Year	Teacher Ratings		Parent Ratings
	Internalizing	Externalizing	Internalizing	Externalizing
Year 7	0	0	0	0
Year 8	−.01(−.34, .32)	−.04(−.36, .28)	--	--
Year 9	−.19(−.14, .51)	.02(−.29, .33)	0.66(.47, .85)	0.36(.21, .51)
Year 10	.11(−.22, .44)	.13(−.13, .40)	0.64(.44, .84)	0.54(.40, .68)
Year 11	.53(.24, .83)	.20(−.07, .47)	0.78(.59, .97)	0.72(.55, .89)
Year 12	.86(.45, 1.26)	.53(.24, .81)	0.80(.65, .95)	0.63(.48, .78)
Year 13	.48(.15, .80)	.83(.44, 1.22)	0.86(.70, 1.02)	0.85(.68, 1.02)
Year 14	.88(.47, 1.30)	.64(.30, .98)	1.06(.86, 1.27)	1.08(.89, 1.28)
Year 15	1	1	1.10(.86, 1.33)	1.42(1.13, 1.70)
Year 16	--	--	1	1

Note. Loadings and 95% confidence intervals (based on Standard errors) for the latent basis growth Slope indicators. In the latent basis growth model parameterization, loadings by each year on the Slope factor can be interpreted as the proportion of that total change at that age that has occurred.

-- indicates that data were not available for that year for that rater.

The externalizing model shown in Figure 1B also fit well, χ²(48)=62.78, p=.074, CFI=.992, RMSEA=.020. The mean of the Slope was significant and negative (μ= –.31, p<.001), also indicating an overall decline in teacher-rated externalizing behaviors from ages 7 to 15, consistent with past research (Keiley et al., 2000). Unstandardized residual variances of the Intercept (ζ=.44, p<.001) and Slope (ζ=.27, p=.022), after accounting for sex, were significant, as was their negative correlation (r=–.44, p=.001).

The estimated Slope loadings (Table III) showed a similar pattern to that found for internalizing scores. Changes were small at ages 8 to 11, and approximately half the total decrease (.53) from age 7 to 15 was evident by age 12; .83 of this decrease had occurred by age 13. There was a slight increase in externalizing behaviors are age 14, evidenced by the lower loading (.64) for this time point compared to those around it.

Parent ratings

The internalizing model shown in Figure 2A fit acceptably, χ²(48)=111.91, p<.001, CFI=.989, RMSEA=.039. The unstandardized mean for the Slope was significant and negative (μ = –.16, p= .010). The unstandardized residual variances (after controlling for sex) for both the Intercept (ζ=.88, p<.001) and the Slope (ζ=.77, p=.001) were significant, as was their negative correlation (r= –.40, p=.008).

Generally, the estimated loadings for the parent-rated internalizing Slope were higher than those for the teacher ratings at each age. Most of the decrease in internalizing change in behavior occurred within the first three years of measurement, in contrast to teacher-rated internalizing behaviors. Specifically, the loading of .66 for age 9 indicated that .66 of the total decrease in parent-rated internalizing behavior from age 7 to 16 had occurred by age 9. The loadings (Table III) exceeded 1.0 for ages 14 and 15, indicating that internalizing behaviors were slightly lower at these ages than at age 16, which had a fixed loading of 1.0.

The externalizing model shown in Figure 2B also fit acceptably, χ²(48)=102.87, p<.001, CFI=.993, RMSEA=.036. The unstandardized mean for the Slope was negative, (μ = –.47, p<.001). Although the unstandardized residual variances (after controlling for sex) for the Intercept (ζ=.72, p<.001) and Slope (ζ=.45, p<.001) were both significant, their correlation did not reach significance (r= –.19, p=.075).

In contrast to the patterns seen with the teacher-rated externalizing scores, and similar to the parent-rated internalizing scores, the early ages showed evidence for substantial decreases in parent-rated externalizing behavior. Specifically, .36 of the total decrease from age 7 to 16 had occurred by age 9, and .54 by age 10. Similar to the parent-rated internalizing scores, the loadings (Table III) exceeded 1.0 for ages 14 and 15, indicating that externalizing behaviors were slightly lower at these ages than at age 16, which had a fixed loading of 1.0.

ACE Growth Models

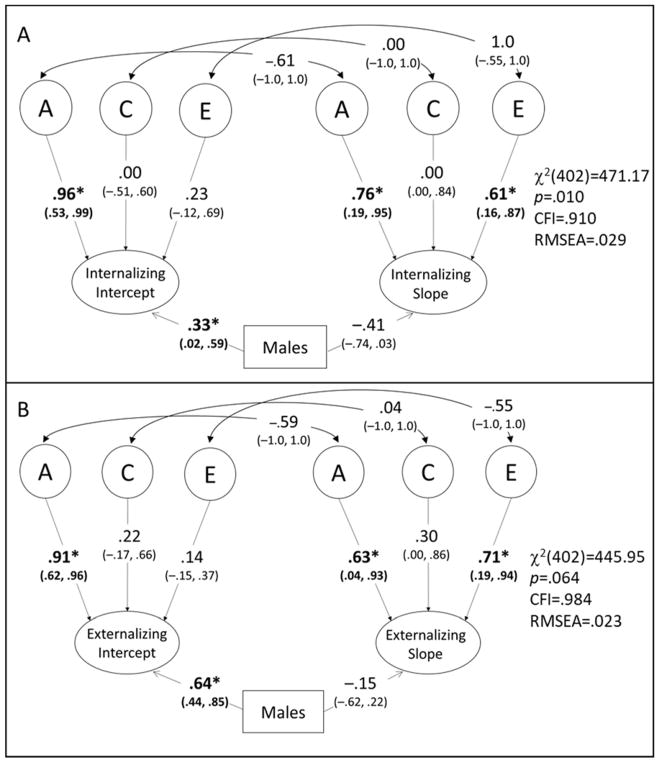
Teacher ratings

Both teacher-rated ACE models are shown in Figure 3, and the twin correlations are given in Table IV. The internalizing model fit was acceptable, χ²(402)=471.17, p=.010, CFI=.910, RMSEA=.029. As shown in Figure 3A, the only significant influence on the internalizing Intercept apart from sex was the A component (β=.96, 95% CI = .53 to .99), explaining 92% of the variation. The Slope showed significant genetic (β=.76, 95% CI =.19 to .95) and non-shared environmental effects (β=.61, 95% CI =.16 to .87). Both the genetic (rA= –.61, 95% CI = –1.0 to 1.0; 90% CI = –1.0 to –.25), and the nonshared environmental (rE = 1.0, 95% CI = –.55 to 1.0; 90% CI = .05 to 1.0) correlations were marginally significant. Although we did not have power to find a significant association, these patterns suggest that genetic influences explain the negative phenotypic association between the Intercept and Slope. Moreover, because the confidence intervals for the rA and rE include –1.0 and 1.0, respectively, there were no genetic or environmental influences unique to the Slope (see also the Cholesky decomposition in Supplementary Figure 1A).

Figure 3.

Teacher-rating ACE models for internalizing (panel A) and externalizing (panel B) behaviors (individual time points on which the latent growth factors are based are not shown for simplicity, but are similar to those shown in Figure 1). Standardized parameter estimates (and bootstrapped 95% confidence intervals) for additive genetic (A), shared environmental (C), and nonshared environmental (E) influences and correlations (rA, rC, and rE) among these factors for the Intercept and Slope factors are presented. The standardized regression betas from sex capture the mean difference across sex (males – females). Model fits are shown to the right of the path models. The Cholesky decompositions from which these parameters were derived are available in Supplementary Figure 1. *p<.05, as indicated by the bootstrapped confidence intervals.

Table IV.

Phenotypic and Twin Correlations (MZ/DZ) For Latent Growth Factors

Growth Factors	Intercept	Slope
Teacher Ratings
Internalizing
Intercept	1.0*a/.33*	−.24
Slope	−.59*/−.02	.91*/−.03
Externalizing
Intercept	.98*/.52*	−.42*
Slope	−.36*/−.18	.49/.29
Parent Ratings
Internalizing
Intercept	.95*/.37*	−.16
Slope	−.26/.27	.80*/.41
Externalizing
Intercept	.83*/.52*	−.15
Slope	.03/.02	.43*/.43*

Note. Partial correlations, controlling for sex. Correlations on the diagonal and in the lower diagonal are cross-twin correlations (MZ on left/DZ on right); those in the upper diagonal are phenotypic correlations (within-individual Intercept-Slope). Correlations taken from a model in which within-twin parameters were constrained to equality across twins and zygosity groups. MZ = monozygotic, DZ = dizygotic.

^aCorrelation was estimated at slightly over 1.0 (1.06), so was bound at 1.0.

^*p<.05.

The externalizing genetic growth model fit well, χ²(402)=445.95, p=.064, CFI=.984, RMSEA=.023. As shown in Figure 3B, the only significant influence on the Intercept other than sex was from the A component (β=.91, 95% CI = .62 to .96), accounting for 83% of the variation in stability for externalizing behavior. The slope showed significant genetic (β=.63, 95% CI =.04 to .93) and nonshared environmental influences (β=.71, 95% CI =.19 to .94). Both the rA and rE derived from this model were negative (rA = –.59, 95% CI = –1.0 to 1.0); rE = –.54, 95% CI = –1.0 to 1.0), but neither reached significance, perhaps due to low power. These correlations suggest that both genetic and nonshared environmental influences explain the negative phenotypic association between the Intercept and Slope. As with the internalizing model, the inclusion of –1.0 in the confidence intervals for rA and rE suggests that there were no genetic or environmental influences unique to the Slope (see also the Cholesky decomposition in Supplementary Figure 1B).

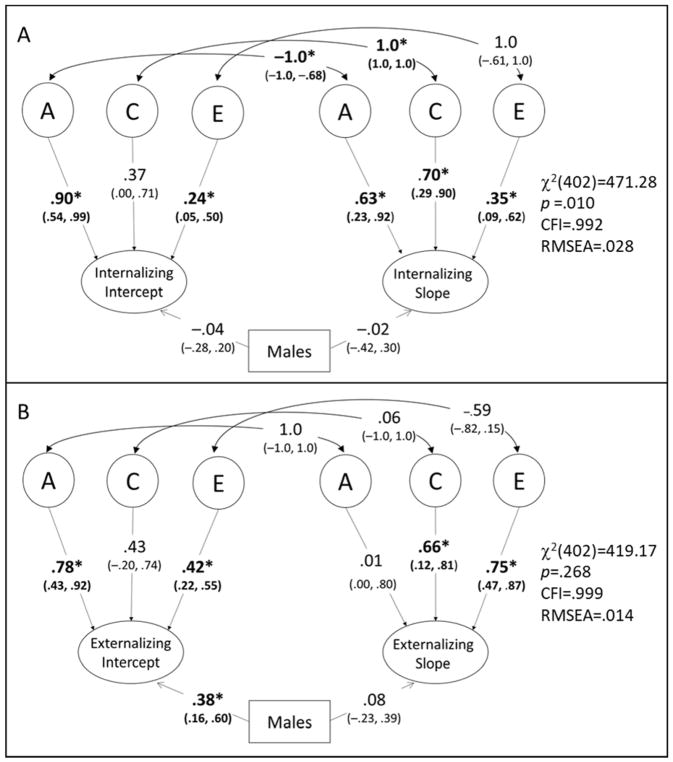
Parent ratings

The parent-rated internalizing growth model fit well, χ²(402)=471.28, p =.010, RMSEA=.028, CFI=.992. As shown in Figure 4A, both genetic (β= .90, 95% CI = .54 to .99) and nonshared environmental (β= .24, 95% CI =.05 to .50) influences were significant for the Intercept; shared environmental influences were marginally significant (β= .37, 95% CI = .00 to .71, 90% CI = .07 to .68). The Slope was significantly influenced by genetic (β=.63, 95% CI =.23 to .92, shared environmental (β=.70, 95% CI =.29 to .90), and nonshared environment factors (β=.35, 95% CI =.09 to .62). Similar to the teacher-rated internalizing problems model, genetic influences accounted for the most variance in the Intercept and those genetic influences on the Intercept were negatively correlated with those for the Slope, but in this model, that genetic correlation was significant (rA = –1.0, 95% CI = –1.0 to –.68). The nonshared environmental variance in the Intercept did not significantly correlate with that for the Slope (rE = 1.0, 95% CI = –.61 to 1.0) but the shared environmental influences on the Intercept were significantly associated with those for the Slope (rC = 1.0, 95% CI = 1.0 to 1.0).

Figure 4.

Parent-rating ACE models for internalizing (panel A) and externalizing (panel B) behaviors (individual time points on which the latent growth factors are based are not shown for simplicity, but are similar to those shown in Figure 2). Standardized parameter estimates (and bootstrapped 95% confidence intervals) for additive genetic (A), shared environmental (C), and nonshared environmental (E) influences and correlations (rA, rC, and rE) among these factors for the Intercept and Slope factors are presented. The standardized regression betas from sex capture the mean difference across sex (males – females). Model fits are shown to the right of the path models. The Cholesky decompositions from which these parameters were derived are available in Supplementary Figure 2. *p<.05, as indicated by the bootstrapped confidence intervals.

Even though the phenotypic correlation between the parent-rated internalizing Intercept and Slope was less than unity (Figure 2A), the specific A, C, and E effects unique to the Slope were all estimated at zero in the Cholesky decompositions shown in Supplementary Figure 2A. Because the genetic and environmental influences on the Intercept predicted the Slope in opposing directions, they summed to a predicted phenotypic correlation less than unity. This result suggests that the division between Slope and Intercept may be accounted for by etiological effects moving in opposite directions, rather than division in the effects of A, C, and E. However, given that genetic influences have the largest impact on the Intercept, the negative genetic correlation accounts for the overall negative phenotypic correlation shown in Figure 2A.

The parent-rated externalizing model also fit the data well, χ²(402)=419.17, p=.268, CFI=.999, RMSEA=.014² . As shown in Figure 4B, consistent with the teacher-rated externalizing model, genetic influences had the largest influence on the externalizing Intercept (β=.78, 95% CI = .43 to .92). Unlike the teacher-rated externalizing model, there were also significant nonshared environmental effects on the Intercept (β= .42, 95% CI = .24 to .55). The Slope showed significant shared environmental (β= .66, 95% CI = .12 to .81) and nonshared environmental effects (β= .75, 95% CI = .47 to .87). However, there were no significant relations between the ACE components for the Intercept and Slope in this model, consistent with the absence of a phenotypic correlation in Figure 2B. In the Cholesky decomposition shown in Supplementary Figure 2B, the Slope had significant nonshared environmental influences independent of those for the Intercept (β=.61, 95% CI = .38 to .73), consistent with the fact that the 95% confidence interval for rE in Figure 4B did not include –1.0 (rE = –.59, 95% CI = –.82 to .15).

Integration across models

Considering all four models together, the ACE decompositions were consistent in showing that (1) the Intercepts were largely genetically influenced whereas the Slopes had more evidence for environmental influences, and (2) genetic influences tended to be negatively correlated across Intercepts and Slopes, whereas environmental influences tended to be positively correlated. The internalizing and externalizing models diverged in that (1) the teacher- and parent-rated internalizing models both showed a marginally significant or significant negative genetic correlation between the Intercept and Slope, whereas (2) the teacher- and parent- rated externalizing models did not show significant etiological correlations for the Intercept and Slope. Finally, the teacher- and parent-rated models diverged in that the parent-rated models nominally showed more evidence for shared environmental influences.

Overlap of Teacher- and Parent-Rated Growth Factors

An important question is to what extent these etiological influences overlap across raters. Because biometric ACE growth models of both raters together were too large to reliably estimate with our sample size (particularly given the ordinal nature of the data), we used factor scores to investigate this question.

We first estimated cross-rater phenotypic correlations, controlling for sex, between the growth factors within each behavior type and extracted factor scores from these two confirmatory factor analyses³ . These cross-rater phenotypic models fit well: for internalizing, χ²(173)=244.01, p<.001, CFI=.988, RMSEA=.022; and for externalizing, χ²(173)=217.12, p=.013, CFI=.995, RMSEA=.017. As shown in Supplementary Table I, the Intercepts and Slopes correlated significantly across raters, with correlations in the low to moderate range (rs=.36 to .64, ps<.001), except for the internalizing Slopes, which were not significantly correlated across raters (r=.07, p=.629). The cross-rater correlations for the factor scores extracted from these models showed the same pattern, as shown in Supplementary Table II. The correlations for the Intercept factor scores were significant (rs=.48 to .54, ps<.001), as was the correlation of the externalizing Slope factor scores (r=.79, p<.001), but not the correlation of the internalizing Slope factor scores (r= –.01, p=.854). Cross-twin-cross-trait correlations of the factor scores are shown in Supplementary Table III.

We then estimated Cholesky decompositions of each growth factor score across rater, controlling for sex (see Table V). The biometric components for these factor scores differed somewhat from those for the latent variables shown in Figures 3–4, likely because of factor indeterminacy. In particular, the factor scores were generally somewhat less heritable and showed more nonshared environmental variance; however, the general qualitative patterns of Intercepts showing more genetic variance than Slopes, and parent ratings showing more shared environmental influences than teacher ratings, were recapitulated in the factor score analyses.

Table V.

Standardized Path Estimates From Cholesky Decompositions of Factor Scores for Parent and Teacher Ratings for Each Growth Factor

Model	a11	a12	a22	c11	c12	c22	e11	e12	e22	rA	rC	rE
Internalizing
Intercepts	.78*	.43*	.47*	.14	.53*	.00	.59*	.21*	.52*	.68*	1.0	.37*
Slopes	.54*	−.17	.31	.01	.51*	.31	.74*	.11*	.71*	−.48	.85	.15*
Externalizing
Intercepts	.70*	.43*	.61*	.32*	.10	.44	.50*	.21*	.39*	.58*	.22	.47*
Slopes	.52*	.40	.29	.42*	.37	.35	.73*	.58*	.41*	.81	.73	.82*

Note. Bivariate Cholesky decompositions of growth factor scores across raters extracted from the models presented in Supplementary Table I. The same bivariate model was run for each growth factor, with teacher ratings first and parent ratings second. Sex was included as a covariate, so the squared ace paths may not sum to 1.0. The structure of the model is similar to that in Supplementary Figures 1 and 2, but with manifest factor scores instead of latent variables, and factor scores only within growth factor (e.g., teacher-rated externalizing Intercept with parent-rated externalizing Intercept). Models fit acceptably, all χ²(23)<39.33, p>.018, CFI>.946, RMSEA<.058. rA, rC, and rE were derived from the same Cholesky decompositions and designated significant if both paths contributing to covariance (e.g., a11 and a12) were significant.

^*p<.05.

Importantly, there was evidence for substantial etiological overlap across raters. Both the internalizing and externalizing Intercepts showed significant genetic (rAs= .68 and .58, respectively) and nonshared environmental (rEs= .37 and .47, respectively) correlations. Although the externalizing Slopes showed a nominally large genetic correlation across raters (rA=.81), it did not reach significance given that the genetic variances for the Slope factor scores were smaller. However, the Slope factor scores did show significant nonshared environmental correlations across raters (rEs=.15 and .82 for internalizing and externalizing Slopes, respectively). Taken together, these results show that there is a significant moderate to large association between growth factors derived from parents’ and teachers’ ratings, particularly the Intercepts or stability components.

Discussion

We fit ACE models to latent growth curve models of teacher- and parent-rated internalizing and externalizing behavior scales to examine the etiology of the growth factors and their covariation. We found that Intercept factors, which capture stability across time, were highly heritable for both internalizing and externalizing, with small and nonsignificant environmental influences for teacher-rated data but significant nonshared environmental influences for parent-rated data. Although only the parent-rated internalizing Slope was significantly genetically associated with the Intercept, the teacher-rated internalizing Slope showed the same nominal pattern. In contrast, the externalizing Slopes did not share significant ACE variance with the Intercepts in either rater. The parent-rated externalizing Slope had significant unique nonshared environmental variance but the teacher-rated externalizing Slope did not. In the following sections, we discuss what these results may mean for developmental psychopathology in general, and internalizing and externalizing problems more specifically.

Stability

Commonality across time is perhaps the most studied aspect of developmental psychopathology. Some have found that psychiatric symptoms as early as age three years predicts adult psychopathology (Caspi et al., 1996), suggesting stability in these behaviors. Most internalizing psychiatric symptoms appear in some sub-syndromal form before they manifest as disorders (Zahn-Waxler, Klimes-Dougan, & Slattery, 2000). In our study, the stability factors (Intercepts) were highly heritable, with genetic influences explaining 81 to 92% of internalizing stability and 61 to 83% of externalizing stability. The fact that stability was heritable agrees with past simplex models. The parent additive genetic estimates on the Intercepts overlap with the confidence intervals from a previous simplex study of mother-reported behavior (Bartels et al., 2004; Huizink et al., 2007; van der Valk et al., 2003). Our confidence intervals on the additive genetic estimates for the Intercept also overlapped with those same parameter estimates a growth curve analysis of mother-rated CBCL anxious/depressed scales for children aged 7, 10, and 12 years (Lubke et al. 2016), demonstrating similar results to those from a much larger sample with greater statistical power.

There were more environmental influences on the Intercepts in both parent-rated models. In particular, both parent-rated internalizing and externalizing stability had significant nonshared environmental influences (6% and 18%, respectively). Because the Intercept is a latent factor reflecting commonality across time, these E variances cannot reflect random measurement error, which would not correlate across time; however they could capture correlated rater bias across time.

Change and its relation to stability

In the current study, we were able to test for etiological effects on change (as assessed with nonlinear Slope factors) as well as stability. Phenotypically, we replicated past findings: The Slope means indicated a decline in externalizing and internalizing behavior, consistent with past research findings on trajectories (Keiley et al., 2000). Thus, the etiological effects on the Slopes are the degree to which genetic and environmental influences affect the rate of nonlinear decline. Prior studies using simplex and common factor models suggest that change (i.e., new variance at later time points) is typically due to nonshared environmental influences, which also include measurement error, but in some cases is also due to age-specific genetic influences (Bartels et al., 2004; Haberstick et al., 2005; Huizink et al., 2007, van der Valk et al., 2003). Our results support this conclusion. Significant and moderate genetic effects on the Slope were found in three models, all but the parent-rated externalizing model, but these effects were highly correlated with the genetic effects on stability (rAs = –.59 to –1.0, with all 95% confidence intervals including –1.0).

There was a general trend, phenotypically and genetically, for negative associations between the Intercept and Slope factors across all models, consistent with our finding that the Intercepts negatively correlated with the Slopes for these behaviors (e.g., Lee & Bukowski, 2012). This pattern suggests that individuals who start out with higher rates of problems tend to show larger decreases in those problems across time. With respect to externalizing behavior phenotypic models, we found that the Intercept significantly correlated with the Slope for the teacher-rated behavior (r = –.44), but not the parent-rated behavior (r = –.19). The ACE model for the teacher ratings did not reveal that any etiological factor significantly accounted for this correlation, although numerically the genetic correlation explained the bulk of the predicted phenotypic correlation (86%, with the remaining correlation explained by E covariance). Although these genetic and nonshared environment correlations were less than unity for the teacher-rated externalizing scores, none of the the estimated unique genetic and environmental variances in the supplementary Cholesky decompositions (accounting for 62% of the total Slope variance) was significant on its own. In contrast, the Slope for the parent-rated data had significant unique E variance (37%), with no genetic influences on the Slope.

The pattern was somewhat different for internalizing behavior. In the phenotypic models, we found that the Intercept significantly correlated with the Slope for both teacher-rated (r = –.41) and parent-rated behavior (r = –.40). For both of these models, these negative correlations were entirely attributable to negative genetic correlations (rA = –.61, p < .10 in the teacher-ratings model, rA = –1.0 in the parent-ratings model, p < .05), although that genetic correlation was only marginally significant in the teacher-ratings model. In both raters’ models, the environmental correlations were positive, though non-significant except for the rC in the parent-ratings model. Moreover, in neither rater’s model was there significant unique A, C, or E variance for the Slope.

Taken together, the models suggest that more etiological influences are shared between the Intercepts and Slopes of internalizing behaviors than between the Intercepts and Slopes of externalizing behaviors. In other words, there are more unique etiological influences on the growth factors of externalizing, while with internalizing the stability and change are influenced by the same factors.

Developmentally informative genetics

Past research utilizing biometrical components to decompose variation in Slopes and Intercepts has found substantial heritability on the commonality. Several traits, including cognitive abilities (Reynolds, Finkel, Gatz, & Pedersen, 2002), Borderline Personality Disorder (Bornovalova, Hicks, Iacono, & McGue, 2009), mothers’ reports of their chidren’s anxious/depressed behaviors (Lubke et al. 2016), and even body mass index (Hjelmborg et al., 2008), have been shown to be more heritable at the level of stability than their cross-sectional measures. This study shows how these general measures of child behavior problems also show substantial heritable influences on stability across time, and this influence is higher than when these constructs are measured at one time point.

Not only are developmental models informative for understanding how genes influence psychiatric phenotypes, they may also inform us on how to increase power in internalizing and externalizing disorders more broadly. In the past, both latent factor models of phenotypes (Kendler & Neale, 2010), and endophentoypes –– intermediate phenotypes that lie closer to genetic mechanisms –– have been proposed as methods to increase power in genetic association studies. One of the key arguments for the latent factor models is that reduction of random error variation will increase power to detect effects generally, including genetic effects (Kendler & Neale, 2010). Across studies, the high heritability of Intercept factors is probably due (in part) to a decrease in error variation by measuring multiple time points. Future studies in both biometrical data sets and molecular genetics may gain power by parameterizing variables that represent stable variation across years of development, rather than using cross-sectional estimates.

Limitations

Although we found converging evidence for heritability of the Intercepts (stability) across raters, each rater in this study has some specific limitations. For example, in teacher ratings we could not control for when twins may have been in the same classroom. However, this would increase the C variation (Towers et al., 2000), which we did not detect in our final latent models. Furthermore, stability in parent-ratings models may be due to rating consistency, considering that each time point was rated by the same parent; in contrast, teachers likely changed yearly, and individual variability of the teacher would not be accounted for in the latent factors.

In addition, parents and teachers interact with children in different environments, though there is evidence for convergence in parent and teacher ratings in estimation of problem behavior heritabilities (Saudino, Ronald, & Plomin, 2005). Our analysis of the growth factor scores across raters indicates there is significant genetic and environmental overlap across raters for the Intercepts, but only significant environmental overlap for the Slopes. However, it also appears that the Intercepts for parent- and teacher-ratings tap some different genetic effects. These differences may reflect differences in contexts or rater bias.

This sample size is also smaller than some past studies of latent growth models, so it is important to consider the size of the confidence intervals for these estimates. We note that there is overlap between our patterns/estimates and those from larger studies of similar behaviors (Lubke et al., 2016). Additional replication with other measures of internalizing and externalizing behavior are needed as well.

Additionally, we find decrease in internalizing across time phenotypically, which is different than what is typically seen in the literature (Keiley et al. 2000). Our overall decrease is likely due to our inclusion of older ages than prior studies, the use of nonlinear procedures that capture this pattern, and use of CBCL/TRF measures. Inspection of the individual time loadings of the latent basis growth model shows an initial increase in internalizing problems and then later decline; this suggests an overall increase or decrease is masking a more nuanced pattern. In these data, depression and anxiety diagnosis increase across time, while internalizing symptoms of the CBCL/TRF decrease. Despite these inconsistencies, diagnosis and checklist measures remain significantly correlated (Johnson, Whisman, Corely, Hewitt, & Rhee, 2012), suggesting validity of the measures, and decrease specific to the CBCL/TRF. Of note, this is only an issue for internalizing as past research has consistently found decreases in externalizing behavior across time using latent growth curve models (Keiley et al., 2000; Gilliom and Shaw, 2004).

Finally, the use of binned variables may have limited our power because it likely further increased the standard errors for model parameters. However, past research has shown this to be a more accurate method to estimate coefficients than transformations in twin models (Derks et al., 2004); moreover, no transformations can correct distributions with a floor effect such as ours, which had a large number of zero and low scores.

Conclusions

Genetic effects on internalizing and externalizing patterns persist beyond variability at a single time point. By using latent growth curve models of internalizing and externalizing behavior rated by teachers and parents, we isolated higher proportions of genetic variation than have been shown cross-sectionally and tested hypotheses of etiological influences contributing to these growth factors and their correlations. These models help explain mechanisms of developmental processes by showing that genetic influences largely influence behavior problems through stability (Intercept) factors, and that internalizing and externalizing behaviors may show similar phenotypic patterns, but show some etiological distinction in their developmental processes.