Skip to main content
. Author manuscript; available in PMC: 2018 Jul 2.
Published in final edited form as: SIAM J Imaging Sci. 2016 Jul 21;9(3):1004–1041. doi: 10.1137/15M1042280

Figure 3. Exact recovery of edge set from the minimum necessary number of Fourier samples.

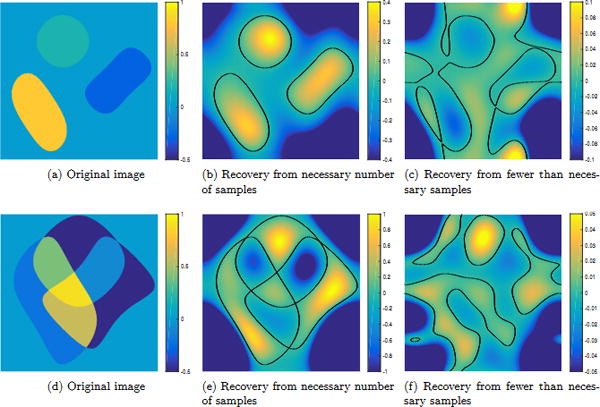
Figure 3

The piecewise constant images shown in (a)&(d) were generated to have edge set given by the trigonometric curve {μ = 0} of degree (6, 6), i.e. the known minimal polynomial μ is described by 7 × 7 coefficients. We recover μ by solving the linear system (18) built from 11 × 11 Fourier samples of the original image, which were approximated numerically to high precision. This is the necessary minimum number of samples specified by Prop. 4, and is less than the sufficient number of samples specified by Thm. 2 (19×19 samples). The recovered minimal polynomial μ is shown in (b)&(e) with {μ = 0} plotted in black; we observe the recovered coefficients match the known minimal polynomial coefficients to within machine precision. In (c)&(f) we show a solution obtained from fewer than the necessary minimum number of samples. Note that in this case the true edge set does not coincide with the zero set of the recovered trigonometric polynomial.