Figure 1.

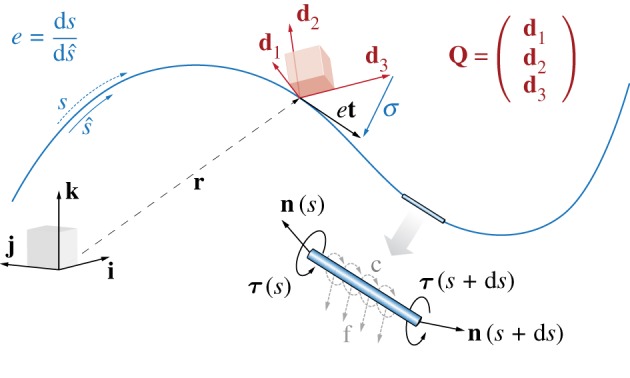
The Cosserat rod model. A filament deforming in the three-dimensional space is represented by a centre-line coordinate r and a material frame characterized by the orthonormal triad {d₁,d₂,d₃}. The corresponding orthogonal rotation matrix Q with row entries d₁, d₂, d₃ transforms a vector x from the laboratory canonical basis {i,j,k} to the material frame of reference {d₁,d₂,d₃} so that ${\mathbf{\text{x}}}_{\mathcal{L}}=\mathbf{\text{Q}}\mathbf{\text{x}}$ and vice versa $\mathbf{\text{x}}={\mathbf{\text{Q}}}^{\mathrm{T}}{\mathbf{\text{x}}}_{\mathcal{L}}$. If extension or compression is allowed, the current filament configuration arc-length s may no longer coincide with the rest reference arc-length $\hat{s}$. This is captured via the scalar dilatation field $e=\mathrm{d}s/\mathrm{d}\hat{s}$. Moreover, to account for shear we allow the triad {d₁,d₂,d₃} to detach from the unit tangent vector t so that d₃≠t (we recall that the condition d₃=t and e=1 correspond to the Kirchhoff constraint for unshearable and inextensible rods, and implies that σ=et−d₃=0). The dynamics of the centre line and the material frame is determined at each cross section by the internal force and torque resultants, n and τ. External loads are represented via the force f and couple c line densities.