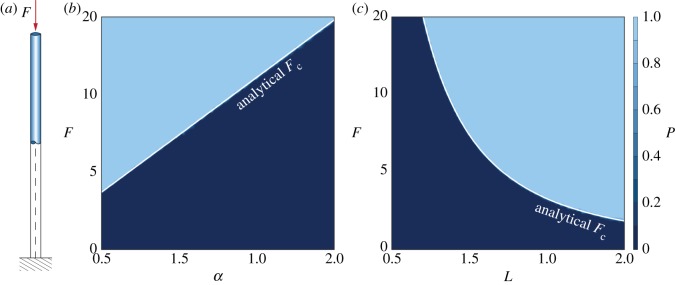
Figure 14.

Euler buckling instability. (a) Inextensible and unshearable rod vertically initialized and subject to the axial load F. (b) Probability P of observing an instability event as a function of the compression force F and the bending rigidity α for a fixed length L=1 m. The corresponding analytical solution is overlaid as reference (white line). (c) Probability P of observing an instability event as a function of the compression force F and the length L for a fixed bending rigidity α=1 Nm². The corresponding analytical solution is overlaid as reference (white line). The probability P is determined by performing 10 simulations for each pair of parameters (F,α) or (F,L). Each simulation is initially perturbed by applying to every discretization node a small random force sampled from a uniform distribution, such that $\parallel F_{\mathrm{R}}\parallel \sim \mathcal{U}(0,{10}^{-2})\hspace{0.17em}\mathrm{N}$. The occurrence of an instability is detected whenever the rod bending energy E_B>E_th with E_th=10⁻³ J. Settings: rod’s mass m_r=1 kg, twist stiffness β=2α/3 Nm², shear/stretch matrix S=10⁵×1 N, bend/twist matrix B=diag(α,α,β) Nm², radius r=0.025L m, discretization elements n=100 m⁻¹, timestep δt= 10⁻⁵ s, simulation time T_sim=10 s, dissipation constant γ=0.