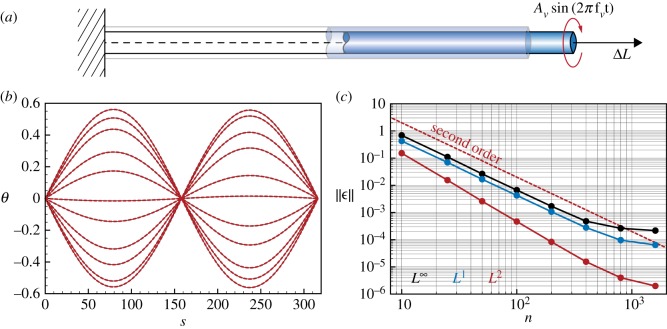
Figure 16.

Time-space convergence study for twist forced vibrations in a stretched rod. (a) We consider a rod clamped at one end, forced to vibrate by applying the periodic couple $A_v\sin (2\pi f_{v}t)$ to the free end, and characterized by rest length $\hat{L}$ which is extended to a final length $L=e\hat{L}$. (b) Comparison between analytical θ (black lines) and numerical θⁿ (red dashed lines) angular displacement with respect to the reference configuration along a stretched rod. Each red (numerical simulation) and black (analytical solution) line corresponds to the angular displacement along a rod discretized with n=1600 elements, and sampled at regular intervals Δt=T_v/10 within one loading period $T_v=f_v^{-1}$. (c) Norms $L^{\mathrm{\infty }}(ϵ)$ (black), L¹(ϵ) (blue) and L²(ϵ) (red) of the error ϵ=∥θ−θⁿ∥ at different levels of time-space resolution are plotted against the number of discretization elements n. Here, the time discretization δt is slaved by the spatial discretization n according to δt=10⁻⁴δl seconds. For all studies, we used the following settings: rod’s density ρ=10 kg m⁻³, Young’s modulus E=10⁶ Pa, shear modulus G=2E/3 Pa, shear/stretch matrix $\widehat{\mathbf{\text{S}}}=\text{diag}(4G\hat{A}/3,4G\hat{A}/3,E\hat{A})\hspace{0.17em}\mathrm{N}$, bend/twist matrix $\widehat{\mathbf{\text{B}}}=\text{diag}(E{\hat{I}}_1,E{\hat{I}}_2,G{\hat{I}}_3)\hspace{0.17em}{\mathrm{Nm}}^2$, forcing amplitude A_v=10³ Nm, forcing frequency f_v=1 s⁻¹, dilatation factor e=1.05, rest length $\hat{L}=\sqrt{E/\rho }/(e{f}_v)\hspace{0.17em}\mathrm{m}$, rest radius $\hat{r}=0.5\hspace{0.17em}\mathrm{m}$, simulation time T_sim=2000 s. We enabled dissipation in the early stages of the simulations, letting γ decay exponentially in time to a zero value.