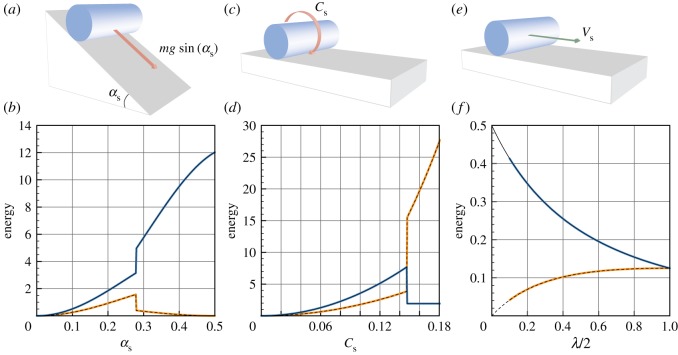
Figure 17.

Rolling static and dynamic friction. (a) A rod initially at rest on a plane inclined of the angle α_s rolls or slips down with linear and angular velocities v and ω due to its own weight mg. (b) Translational E_T=mv²/2 (analytical solution: black line, numerical solution: blue line) and rotational E_R=Jω²/2 (analytical solution: dashed black line, numerical solution: orange line) energies are plotted against the angle α_s. Settings: length L=1 m, radius r= 0.025 m, mass m=1 kg, Young’s modulus E=10⁹ Pa, shear modulus G=2E/3 Pa, shear/stretch matrix S=10⁴×1 N, bend/twist matrix B=diag(EI₁,EI₂,GI₃) Nm², dissipation constant γ=10⁻⁶ kg (ms)⁻¹, gravity g=9.81 m s⁻², static and kinetic friction coefficients μ_s=0.4 and μ_k=0.2, friction threshold velocity $v_{ϵ}={10}^{-4}\hspace{0.17em}\mathrm{m}\hspace{0.17em}{\mathrm{s}}^{-1}$, ground stiffness and viscous dissipation k_w=10 kg s⁻² and γ_w=10⁻⁴ kg s⁻¹, discretization elements n=50, timestep δt= 10⁻⁶ s, simulation time T=0.5 s. (c) Rod set in motion by the external couple C_s on a horizontal plane. (d) Translational E_T and rotational E_R energies are plotted against the couple C_s. Colour scheme and settings are identical to those of panel (b) except for the simulation time T=1 s. (e) Rod with initial velocity V _s slows down due to kinetic friction until the no slip condition is reached. (f) Translational E_T and rotational E_R energies are plotted against the relative mass moment of inertia ratio λ/2. Colour scheme and settings are identical to those of (b) except for the simulation time T=2 s, and the friction threshold velocity v_ϵ=10⁻⁶ m s⁻¹.