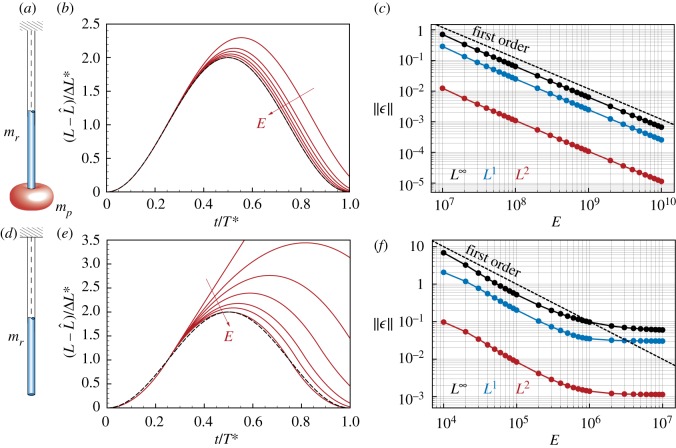
Figure 4.

Vertical oscillation under gravity. (a,d) We consider a vertical rod of mass m_r clamped at the top and with a mass m_p attached to the free end. Assuming that the rod is stiff enough (i.e. $k\simeq \hat{A}E=\text{const}$), it oscillates due to gravity around the equilibrium position $\hat{L}+\mathrm{\Delta }{L}^{\ast }$, where ΔL*=g(m_p+m_r/2)/k with a period $T^{\ast }=2\pi \sqrt{(m_p+m_r/\xi )/k}$ with ξ≃3 for m_p≫m_r, and ξ≃π²/4 for m_p≪m_r. Therefore, the rod oscillates according to $L(t)=\hat{L}+[1+\sin (2\pi t/T^{\ast }-\pi /2)]\mathrm{\Delta }{L}^{\ast }$. (a–b) Case m_p≫m_r with m_p=100 kg and m_r=1 kg. (b) By increasing the stiffness E=10⁷, 2×10⁷, 3×10⁷, 5×10⁷, 10⁸, 10¹⁰ Pa, the simulated oscillations (red lines) approach the analytical solution (dashed black line). (c) Convergence to the analytical solution in the norms $L^{\mathrm{\infty }}(ϵ)$ (black), L¹(ϵ) (blue) and L²(ϵ) (red) with ϵ=∥L(t)−L^E(t)∥, where L^E is the length numerically obtained as a function of E. (c–d) Case m_p≪m_r with m_p=0 kg and m_r=1 kg. (e) By increasing the stiffness E=10⁴, 2×10⁴, 3×10⁴, 5×10⁴, 10⁵, 2×10⁵, 10⁹ Pa, the simulated oscillations approach the analytical solution. (f) Convergence to the analytical solution in the norms $L^{\mathrm{\infty }}(ϵ)$, L¹(ϵ) and L²(ϵ) as a function of E. For all studies, we used the following settings: gravity g=9.81 m s⁻², rod density ρ=10³ kg m⁻³, shear modulus G=2E/3 Pa, shear/stretch matrix $\widehat{\mathbf{\text{S}}}=\text{diag}(4G\hat{A}/3,4G\hat{A}/3,E\hat{A})\hspace{0.17em}\mathrm{N}$, bend/twist matrix $\widehat{\mathbf{\text{B}}}=\text{diag}(E{\hat{I}}_1,E{\hat{I}}_2,G{\hat{I}}_3)\hspace{0.17em}{\mathrm{Nm}}^2$, rest length $\hat{L}=1\hspace{0.17em}\mathrm{m}$, rest cross-sectional area $\hat{A}=m_r/(\hat{L}\rho )\hspace{0.17em}{\mathrm{m}}^2$, number of discretization elements n=100, timestep δt=T*/10⁶, dissipation constant γ=0.