The BaMM web server for de-novo motif discovery and regulatory sequence analysis

Abstract

The BaMM web server offers four tools: (i) de-novo discovery of enriched motifs in a set of nucleotide sequences, (ii) scanning a set of nucleotide sequences with motifs to find motif occurrences, (iii) searching with an input motif for similar motifs in our BaMM database with motifs for >1000 transcription factors, trained from the GTRD ChIP-seq database and (iv) browsing and keyword searching the motif database. In contrast to most other servers, we represent sequence motifs not by position weight matrices (PWMs) but by Bayesian Markov Models (BaMMs) of order 4, which we showed previously to perform substantially better in ROC analyses than PWMs or first order models. To address the inadequacy of P- and E-values as measures of motif quality, we introduce the AvRec score, the average recall over the TP-to-FP ratio between 1 and 100. The BaMM server is freely accessible without registration at https://bammmotif.mpibpc.mpg.de.

INTRODUCTION

Many methods such as ChIP-seq or high-throughput SELEX (1) produce a set of nucleotide sequences that are preferentially bound by a protein of interest in vitro or in vivo. From such data, a motif model for the sequence dependence of the binding affinity of the protein to the DNA or RNA can be derived. This model can then be used to predict binding sites and their strengths in other sequences.

Position weight matrices (PWMs) are the standard model to describe binding motifs. In the PWM every motif position contributes additively and independently from other positions to the total binding energy. Even though the approximation of independence of positions works well for many transcription factors, dependencies do occur (2,3), for example due to bendability or shape constraints during binding (4), to multiple binding configurations of the protein (5), or to cooperative interactions between closely binding factors that can modulate each others’ binding affinities (6).

PWMs can be generalized to Markov models of order k that account for nucleotide dependencies by conditioning the probability for the four nucleotides at each motif position on the previous k nucleotides. First-order Markov models have been added to the popular motif databases JASPAR and HOCOMOCO (7,8). Models of order 2 and higher have not yet been adopted in the major databases, probably due to the difficulties to robustly train the many parameters of these models on limited data.

We recently developed Bayesian Markov Models (BaMMs) (9), which efficiently prevent overfitting by automatically learning conditional probabilities only up to an order k at which they can still be estimated reliably. The key idea is that the conditional probabilities of order k − 1 are used as prior probabilities for the conditional probabilities of order k. We have shown that BaMMs of order 4 and 5 systematically outperform PWMs and first-order models in distinguishing bound sequences from negative sequences generated by a second-order Markov model (9).

A very popular web server for regulatory sequence analysis based on PWMs offering a wide choice of tools is the MEME server (10). The RSAT web server (11) provides a general toolbox for the analysis of regulatory sequences including motif-based analyses. Furthermore, other web resources and databases are available for training first-order models (12,13).

The BaMMmotif server brings the improved quality of BaMM motif models within reach of users unfamiliar with command-line tools, in a largely self-explanatory web interface designed for ease of use. The user can discover BaMM models enriched in a set of input sequences, scan sequence sets with BaMM models for motif occurrences, and compare discovered or uploaded motifs with a database of BaMM models learned from ChIP-seq datasets.

BAMM TOOLS

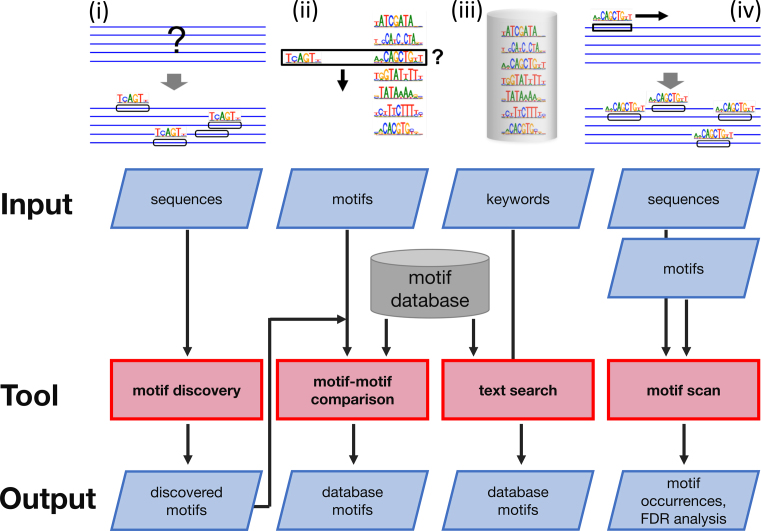
In the following we describe the four tools offered by the BaMM server (Figure 1).

Figure 1.

Tools offered by the BaMM server: (i) de-novo discovery of motifs enriched in a nucleotide sequence set. Motifs are represented by higher order BaMMs, which capture correlations between nucleotides. (ii) Searching with an input BaMM or PWM motif for similar motifs in our database of over 1000 fourth-order BaMM motifs. (iii) Browsing and keyword searching in our motif database. (iv) Scanning a set of nucleotide sequences with BaMM or PWM motifs to find motif occurrences.

De-novo motif discovery using higher-order BaMMs

This tool discovers the motifs enriched in an input set of nucleotide sequences in comparison to the expectation from a background model. For example in sequences obtained from a ChIP-seq or HT-SELEX experiment, the BaMM motif models will approximately describe the sequence dependence of the binding energy of the protein to DNA (see page 2 of supplementary material in (9)). The motif model can be used to scan other sequences for motif occurrences (see next subsection).

Method

The motif discovery proceeds in two stages, seed pattern discovery and motif refinement. For the pattern discovery we developed a fast and sensitive algorithm (PEnGmotif) that will be described in detail elsewhere. Briefly, it finds all locally optimal W-mers (default W = 8) over an alphabet of 11 IUPAC letters (A, C, G, T, R = A or G, Y = C or T, W = A or T, S = C or G, M= A or C, K = G or T, N = A, C, G or T), where locally optimal patterns are those for which changing any single one of its letters would result in a decreased enrichment relative to the random expectation from the background model. (Alternatively, the P-value or the mutual information between presence/absence of motifs and input versus background sequence can be optimized.) With each locally optimal pattern, a PWM of length W is initialized and optimized using an expectation maximization (EM) algorithm. PWMs that have very similar overlapping regions are merged and ranked by our new AvRec score (next section).

The seed motifs are then refined using BaMM!motif (9). It learns the parameters of the BaMMs with an EM algorithm that maximizes the log likelihood of the motif model under a zero-or-one-occurrence-per-sequence (ZOOPS) model (14). The BaMM server offers to train motifs of up to fourth order.

By default, BaMM learns a second order Markov model from the input sequences as a background model. The background model is needed first in the motif discovery to model the sequence stretches not modeled by the motif model and second in the motif quality assessment step to generate negative sequences to estimate motif occurrence P-values. A second order model is generally preferable to first or zeroth order as it can better describe sequence biases observed in open versus closed chromatin, ChIPped versus unChIPped sequences etc. (15). A model of order 1 or 0 is recommended for the discovery of very short motifs (e.g. four to five nucleotides) such as to RNA-binding sites, as such short motifs could be learned to some extent even by a second order background model, severely reducing the sensitivity to discover them.

Usage of de-novo motif discovery

After uploading a FASTA file of up to 50 MB with the input sequences, the motif discovery can be started. A drop-down menu offers advanced options in four categories: general settings, seeding stage, model refinement stage and settings for plots and analyses.

In the general settings category the user can choose whether the motif can be present on both strands, set the order of the background model (default 2) and upload an optional sequence set to train the background model on. Settings of the seeding stage include the initial pattern length W, the z-score significance threshold for refining a motif, and the objective function to optimize in the search for locally optimal patterns. For the refinement stage the user can choose the motif model order (default 2) and the number of flanking positions on the left and right of the core model found in the seed stage. Finally, the user can choose to skip motif scanning, motif performance evaluation or motif annotation, and change the significance thresholds for scanning and annotation.

By default up to four best-performing seed patterns are refined to higher-order models. Seed patterns are ranked by their average recall (AvRec) score (see below). Alternatively, the user can choose to select seed patterns manually for refinement after the seeding stage.

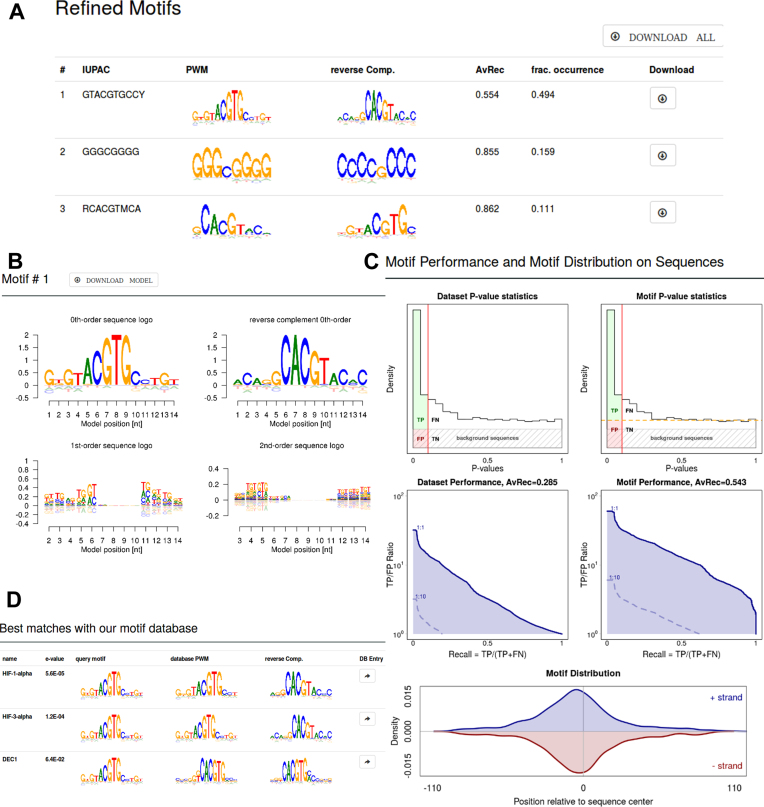
The results page (Figure 2A) lists in a summary table the discovered enriched motifs with their IUPAC patterns, the sequence logos of the 0th-order model (forward and reverse complement), the AvRec motif quality score and the fraction of sequences with motifs (‘frac. occurrence’), estimated using the fdrtool (16) (explained in subsection ‘Dataset AvRec and motif AvRec’). By clicking on the motifs or scrolling down, detailed results for the motifs are shown: 0th-order (forward and reverse complement), first- and second-order sequence logos (Figure 2B); four motif quality assessment plots and a plot of the positional distribution of the motif occurrences relative to the center of the sequences (Figure 2C). (Sequences do not have to be of the same length.) Clicking on the download button in the summary table above saves a zip file containing motif files in BaMM format with the extension ihbcp and all analysis plots for the motif. Last, the database motifs found similar to the discovered motif are listed (see ‘motif-motif comparison’ below) with links to the database entry (‘Best matches with our motif database’, Figure 2D). The results page can later be retrieved by giving the job ID on the ‘Find my job’ page. Results are stored for up to 3 months.

Figure 2.

Selected results from a de-novo motif discovery run. (A) Summary table of discovered motifs. (B) Sequence logos of order 0, 1 and 2 for one discovered motif. (C) Motif quality analysis and positional distribution. In the dataset-centered analysis (left) all input sequences are defined as positives. In the motif-centered analysis (right), only input sequences carrying a motif occurrence are positives. Their fraction is estimated using fdrtool (orange broken line on the upper right). The quality of motifs is quantified by average recall (AvRec), the blue area under the TP-to-FP-versus-recall curves. The curves for positive-to-negative ratios in the dataset of 1:1, 1:10 and 1:100 are plotted. Recall = TP/(TP + FN), where TP = true positives, FP = false positives, FN = false negatives. Positional distribution of the motif occurrences relative to the center of the sequences is shown on the bottom. (D) List of database motifs similar to discovered motif.

Scan sequences for motif occurrences

A set of input sequences can be scanned with a motif or a set of motifs for motif occurrences. The input motifs can be in MEME (version 4 and above) or BaMM format and could have been discovered de-novo by BaMM or they could come from the BaMM database or some other database.

We developed a motif scanning tool that evaluates the log odds score for BaMMs (and PWMs) of any order. A table with the motif occurrences can be downloaded in a zip file, together with the motif analysis on the supplied sequences. The table of motif occurrences contains in each line the sequence length, motif position, binding sites, P-value, and E-value of the occurrence. The P-values are computed by maximum-likelihood fitting of the high-scoring tail of the log-odds score distribution on sequences generated with the background model with an exponential function, which gave good fits (see PhD thesis at https://edoc.ub.uni-muenchen.de/21504/). Each motif is also evaluated using the dataset and motif-based average recall (AvRec, see below) and the positional distribution of the motif occurrences around the center of the sequences (Figure 2C).

BaMM motif database

Our database contains 1021 fourth-order BaMMs trained on ChIP-seq datasets of 620 human transcription factors (TFs), 345 mouse TFs, 19 rat TFs, 16 zebrafish TFs and 21 yeast TFs from the GTRD database (17). For each motif, a meta table, details with higher-order sequence logos, positional enrichment around the centers of training sequences, and motif quality assessment plots, evaluated on the ChIP-seq training sequences, are presented. The user can browse the database or perform a text search through the list of names of the transcription factor.

Search with query motifs through the motif database

This tool searches for motifs in our BaMM motif database that are similar to the query motifs (in MEME or BaMM format). This motif-motif search is automatically run after de-novo motif discovery using each of discovered motifs as query. The query motifs can also be provided by the user. The output of this tool is shown in Figure 2D.

Motif-motif similarities are computed between the zeroth order contribution of the motifs. The distance between two motifs is the minimum distance for any gapless alignment of their columns that leaves at least four columns aligned. The similarity between aligned motifs M₁ and M₂ is defined as

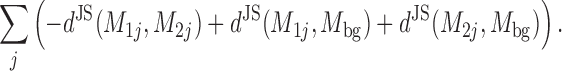Here, the sum runs over all aligned columns j. d^JS(M_1j, M_2j) is the Jenssen-Shannon divergence between the four nucleotide probabilities of model 1 and of model 2 at aligned column j, and M_bg is the zeroth order background distribution in the set on which the query model was learned.

The E-values for the motif-motif matches are computed from these similarity scores by fitting the density of scores computed between 100 randomized query motifs and the databases motifs and fitting the high-scoring tail with an exponential distribution (see PhD thesis of Anja Kiesel at https://edoc.ub.uni-muenchen.de/21504/). The randomization of the query motif is achieved by exchanging A with T probabilities of each position with probability 0.5, and analogously for C and G. In addition columns within 2 positions of each other were randomly swapped. This motif randomization keeps the local GC vs. AT content conserved. In our benchmarks, this score performed as well as the best of the TOMTOM scores (Pearson correlation) (18). An example of results of the motif search is shown in Figure 2D.

MOTIF QUALITY ASSESSMENT AND RANKING

P-values do not assess biological relevance of motifs

P-values and E-values have a severe drawback for ranking motif models: They can be very significant and yet the motifs have no biological relevance at all. For a fixed x-fold enrichment of motif occurrences on the input set in comparison to the background model, the P-value decreases exponentially with the number of sequences in the zero-or-one-occurrence-per-sequence (ZOOPS) model. For that reason, even biologically irrelevant motifs with very slight enrichment factors (e.g. 1.1) can obtain an extremely significant E-value if the input set is large enough. Small enrichment factors can occur frequently in practice simply due to an imperfect background model that slightly underestimates the expected frequency of occurrence.

Precision, recall and false discovery rate

To get a more relevant measure of how well the motif model can separate sequences with a motif (positives) from the background sequences (negatives), we first generate for each input sequence one random sequence of the same length sampled with the second-order Markov background model learned from the input sequences. The score for an input or background sequence is the maximum of the log odds scores of the BaMM over all possible motif positions (ZOOPS model). Every sequence with a score above a cut-off is predicted to carry a motif. We rank all sequences by their score and, for each cut-off score, we count the number of correct predictions above that score, called true positives (TP), and the number of incorrect predictions above the cut-off score, called false positives (FP). The precision is the fraction of predictions that are correct, TP/(TP + FP), and the recall (=sensitivity) is the fraction of positive sequences that are actually predicted, TP/(TP + FN). The false discovery rate is FDR = 1 − precision = FP/(TP + FP).

If we did this analysis on the same sequences from which we had trained the model, we could easily overestimate the motif model performance by overtraining. We therefore use four-fold cross-validation to assess the motif model performance: We split the input and background sequences into four equal-sized parts, retrain the model on three. The results from the four hold-out sets are then combined.

The AUPRC assesses models partly in irrelevant regimes

The area under the recall-precision curve (AUPRC) (see Supplementary Figure S2B) can be interpreted as mean model recall (=sensitivity) averaged over the entire range of precision from 0 to 1. Consider two models: one achieves a maximum precision of 0.99 and the other achieves at any recall a 1% higher precision, with a maximum at 0.9999. Even though the two models have AUPRCs that only differ by 1%, their minimum false discovery rates differ by two orders of magnitude (0.01 and 0.0001), which can make a huge difference in practice.

Consider two application cases. In the first, the expected ratio of sequences with and without true binding sites is ∼1:1, e.g. for a ChIP-seq experiment, and in the second case it is 1:100, e.g. when scanning 10⁴ promoter regions in the human genome for motif occurrences, of which 100 are expected to carry the motif. In the first case, an FDR of 0.1, determined at ratio 1:1 between positive and negative (background) sequences, is quite satisfactory to identify sequences with true binding sites. In the second case, an FDR of 0.1 would result in 0.1 × 10⁴ = 1000 false predictions, which would swamp the expected 100 true binding occurrences. A model with an FDR of 0.001 determined at ratio 1:1 between positive and negative sequences would give us 0.001 × 10⁴ = 10 false predictions, which would result in an acceptable FDR of 10/110.

So the FDR (estimated for a ratio 1:1 of positives to negatives) that is relevant to assess the quality of motif models depends on the application, more precisely, on the expected ratio of positives to negatives in the sequence data. In contrast, the AUPRC puts much weight on very high FDRs, e.g. the range between 0.9 and 1 has as much weight as the range between 0 and 0.1. Another popular measure, the area under the receiver operator curve (AUROC), can be shown to be even less relevant and difficult to interpret for motif model assessment.

Average recall (AvRec)

We sought a motif quality analysis plot and associated quality measure (i) that covers the range of FDRs most relevant in practical applications and (ii) that allows the user to easily estimate the performance of the motif in her particular application, that is, given the ratio between positive and negative sequences expected for her application.

We replace the precision in the precision-recall plot by log₁₀ of the ratio R = TP/FP between true and false positives, log₁₀TP/FP (Figure 2C, middle). From the ratio R one can immediately obtain the false discovery rate, FDR = 1/(1 + R), and vice versa, R = (1 − FDR)/FDR. R = 100 corresponds to FDR = 1/101, R = 1 corresponds to FDR = 0.5. We define the AvRec quality measure as the average recall computed over a range of log₁₀R-values from 0 to 2, which corresponds to an FDR-range from 1/101 to 0.5. We argue that this range of FDRs is most relevant in practice, as illustrated by the two previous examples.

The new quality measure also satisfies the second requirement. The user can simply pick the curve in the AvRec plot that corresponds to the ratio of positive to negative sequences that she expects in her application. Nicely, the curve at ratio 1:10 is the curve at ratio 1:1 shifted down by one unit (log₁₀10), because R is proportional to the ratio of positive to negative sequences in the dataset: When the number of negative sequences is amplified by 10, the number of false positive predictions will also be increased by a factor of 10. On the web server, we show the curves with ratios of 1:1, 1:10 and 1:100 (if visible on the y-scale).

Dataset AvRec and motif AvRec

We used two definitions of positive and negative sequences. In the dataset-centered analysis (Figure 2C, left), the true positive sequences are all sequences from the input set above the cut-off score and the false positive sequences are all background sequences above the cut-off score. The upper left plot in Figure 2C shows the distribution of the motif occurrence P-values computed from their scores. The curve below shows the log₁₀TP/FP values over the recall for this definition of true and false positives.

In the motif-centered analysis (Figure 2C, right), we consider only those sequences as true positives that actually contain a motif instance. In order to estimate the number of TPs for a given score cut-off, we first estimate the fraction of input sequences that contain motif instances using the fdrtool (16). This tool assumes that the negative sequences in the positive set are uniformly distributed over all P-values between 0 and 1 and fits a horizontal line giving the fraction of negatives in the input set to the distribution (orange broken line in Figure 2C, top right). The definition of TPs and FPs illustrated in the top right graph of Figure 2C results in the motif-based AvRec analysis plot below.

When the fraction of motifs in the input sequences is near 100%, both approaches yield very similar results. But when this fraction is small, the motif model may still be very accurate. The motif-centered analysis takes account of that, while the dataset-centered analysis severely underestimates the model performance in these cases.

DOCUMENTATION, USABILITY AND SPEED

Each input parameter is briefly explained in a mouse-over text. A detailed documentation is accessible via the ‘Documentation’ tab on the top of each page. A motif discovery run with 10k (100k) sequences of length 200nt takes around 3.0 (12.5) min. Scanning 100k sequences of length 200nt on both strands for motif matches takes about 6 min per three motifs. A motif-motif search through the largest subcollection of motifs in our database (620 models) takes around 3.5 min per three motifs.

IMPLEMENTATION

The BaMM web server is built on the Django Web framework using Nginx as reverse proxy. Jobs are scheduled via Celery’s asynchronous task queuing system, with the help of Redis as a message broker, and executed on a Linux computer with 28 physical cores using 4 cores per job. MySQL is used as back end database to store results and job parameters. The web front end, back end and the database run in separate Docker containers, enabling easy deployment (Supplementary Figure S1).

CONCLUSION

We hope the BaMM web server will enable many users to exploit the greater descriptive power of BaMMs for motif discovery and regulatory sequence analysis. In the future we will work on extending the database of motifs, especially by training on HT-SELEX datasets.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

German Federal Ministry of Education and Research (BMBF) within the frameworks of e:Bio [SysCore, project 0316176A]; SPP 1935 (project CR 227/6-1) of the German Research Foundation (DFG); International Max Planck Research School for Genome Science (IMPRS-GS). Funding for open access charge: Institutional.

Conflict of interest statement. None declared.