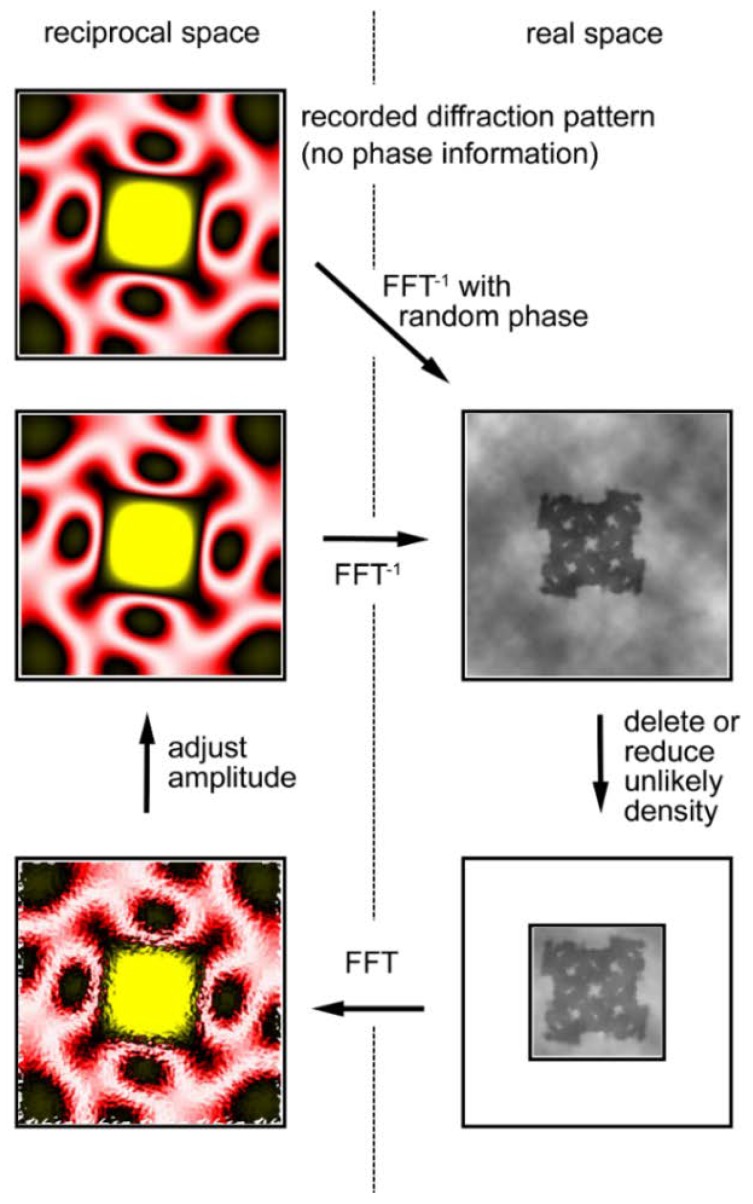
Figure 9.

Iterative phase-retrieval algorithm (oversampling method). The recorded diffraction pattern from a specimen (in reciprocal space, its phase information is missing) is given a random set of phases (Top left). Then the pattern is subjected to inverse Fourier transformation (FFT⁻¹) to obtain the real-space image (electron density distribution) of the specimen (Top right). This is incorrect because of the incorrect set of phases and it has densities in unlikely positions. Usually the approximate size of the specimen is known and we assume this area is likely to contain the specimen. This area is called a support (the smaller square) and is assumed to be somewhat greater than the expected size of the specimen. To successfully retrieve the correct phase information, the entire area of data collection (the larger square) must be at least 2× greater than the actual size of the sample. This is to ensure that the sampling frequency of data is at least 2× finer than the Nyquist frequency, which is defined as f = 1/s, where s is the size of the specimen (This is why it is called the oversampling method). Next, the densities that fall outside the support are reduced either to zero (error-reduction algorithm) or to a small fraction of the obtained densities (hybrid input-output algorithm or HIO algorithm) (Bottom right). After this, a Fourier transformation is applied to this corrected image to obtain a new diffraction pattern (Bottom left). This has a set of phases that is expected to be more correct than the initial set. By retaining this set of phases, the amplitudes are adjusted to the recorded values (Middle left) and the calculations are repeated in a clockwise direction. If all the conditions are right, the image of the sample converges to the true one after hundreds to thousands of iterations. Based on Reference [62].