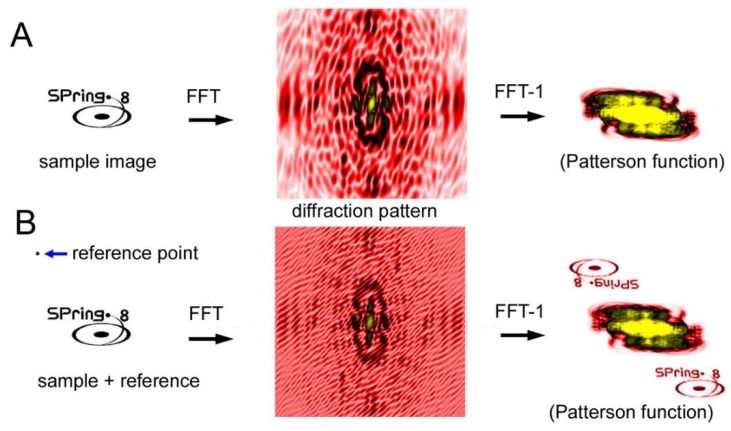
Figure 10.
Principle of Fourier transform holography (FTH). (A) Diffraction from a sample (SPring-8 logo) and its inverse Fourier transformation (FFT−1) calculated by assuming that the phases are all zero. This results in what is called the Patterson function, which is an autocorrelation function of the sample. This is a real-space image but it is very difficult to imagine what the sample looks like by watching this function. (B) Diffraction from a sample with a reference point. The phase information is preserved in the Moiré pattern (caused by the interference between the sample and the reference) and, as a result, the real-space image of the sample is restored by performing inverse Fourier transformation. This is an experiment on a computer.