Abstract
Magnetic guidance of cochlear-implant electrode arrays during insertion has been demonstrated in vitro to reduce insertion forces, which is believed to be correlated to a reduction in trauma. In those prior studies, the magnetic dipole-field source (MDS) was configured to travel on a path that would be coincident with the cochlea’s modiolar axis, which was an unnecessary constraint that was useful to demonstrate feasibility. In this paper, we determine the optimal configuration (size and location) of a spherical-permanent-magnet MDS needed to accomplish guided insertions with a 100 mT field strength required at the cochlea, and we provide a methodology to perform such an optimization more generally. Based on computed-tomography scans of 30 human subjects, the MDS should be lateral-to and slightly anterior-to the cochlea with an approximate radius (mean and standard deviation across subjects) of 64 mm and 4.5 mm, respectively. We compare these results to the modiolar configuration and find that the volume of the MDS can be reduced by a factor of five with a 43% reduction in its radius by moving it to the optimal location. We conservatively estimate that the magnetic forces generated by the optimal configuration are two orders of magnitude below the threshold needed to puncture the basilar membrane. Although subject-specific optimal configurations are computed in this paper, a one-size-fits-all version with a radius of approximately 75 mm is more robust to registration error and likely more practical. Finally, we explain how to translate the results obtained to an electromagnetic MDS.
Keywords: Cochlear implant, robot-assisted surgery, magnetics, optimization
1. Introduction
Cochlear implants are neural-prosthetic devices implanted into the cochlea to directly stimulate the auditory nerve, bypassing the hearing mechanics of the auditory system and restoring effective hearing to those with profound sensorineural hearing loss. During the surgery, the surgeon either drills a hole in the cochlea (known as a cochleostomy) or makes an incision into the round-window membrane to insert an array of electrodes embedded in silicone, commonly referred to as the “electrode array” (EA), into the scala tympani chamber of the cochlea.
The insertion of the EA is known to cause intracochlear damage if the insertion forces exceed the inherent strength of the tissue [1]. The most traumatic damage occurs if the EA perforates the basilar membrane and deviates into the adjacent scala. The usual site for such trauma is along the basal (first) turn, where contact with the lateral wall sometimes defects the electrode-array tip (EAT) out-of-plane and into the basilar membrane [1–3]. This type of trauma is a strong predictor for permanent loss of residual hearing [4]. Evidence also suggests that hearing outcomes improve by avoiding this type of trauma [5]. Preservation of residual hearing and reduction of insertion trauma is now a strong priority in cochlear implantation.
We previously developed a method to magnetically guide the EAT through the scala tympani during EA insertion, using an external magnetic dipole-field source (MDS) to apply the necessary magnetic torque to the EAT to actively bend it away from the walls of the scala tympani (Fig. 1) [6]. Repeatable automated insertions have recently been conducted in at-scale scala-tympani phantoms, designed with simulated cochleostomy and round-window openings [7], using clinical lateral-wall type EAs with magnets embedded at their tips [8]. Insertion forces were reduced by as much as 50% compared to nonguided insertions, and at the first turn in the basal plane, where a high percentage of basilar-membrane perforations occur, the EAT was never in contact with the lateral wall.
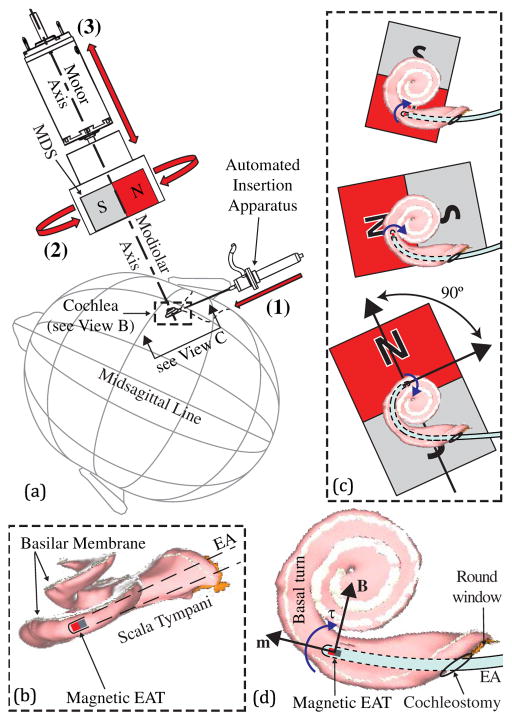
Fig. 1.
(a) In our original concept, magnetically guided insertions are achieved using three controlled degrees-of-freedom: (1) insertion of an EA with a magnetic tip; (2) rotation of the MDS about the modiolar axis to adjust the angle of the applied magnetic field B at the EAT; and (3) translation of the MDS along the modiolar axis to adjust the strength of the magnetic field at the EAT. (b) Close-up view of the scala tympani with the basilar membrane labeled (and shaded in white) so as to show its location relative to the EA and the MDS. (c) At each step of the insertion, the MDS applies torque to the EAT, bending the tip away from the cochlear walls. To minimize attractive force on the EAT toward the MDS, the angle between the magnetic orientations is maintained at approximately 90°. The increasing size of the MDS indicates that it is advancing toward the cochlea with increasing torque generation on the EAT. (d) Close-up view of basal plane, illustrating torque generation. Scala-tympani images are generated from software provided to the public by Eaten-Peabody Laboratory (Boston, MA).
The bending torque that is applied to the EAT is given by the equation
| (1) |
where τ is the torque in units {N·m}, m is the dipole moment of the magnet at the EAT in units {A · m2}, and B is the magnetic field vector at the EAT in units {T} (Fig. 1(d)). As illustrated in Fig. 1(b), the path of the EAT is mostly constrained on a plane orthogonal to the modiolus, particularly for the first turn, with a gradual climb in the direction of the modiolus; we will refer to this as the basal plane. Therefore, to bend the tip around the critical first turn where the EAT would normally contact the lateral walls, the component of the torque vector parallel to the modiolar axis should be maximized so as to bend the EAT principally within this plane. In other words, we want to minimize any component of the torque that could bend the EAT out of the plane and into the basilar membrane. This is accomplished by generating a magnetic-field vector that rotates on the basal plane while leading the EAT’s dipole moment by up to 90°. All of our prior work achieved this by configuring the trajectory of the MDS to rotate about and translate along the modiolar axis (Fig. 1(a)), which we will refer to as the modiolar configuration. However, there is an advantageous reason for the MDS to approach the patient along a different trajectory: the size of the MDS can be reduced by positioning it closer to the cochlea. Our goal in this paper is to generate the required bending torque on the EAT from any location or trajectory that offers a clinical advantage, without the previous constraints placed on the MDS.
It has been shown that a rotating magnet, positioned anywhere relative to a fixed point in space, can generate at this fixed point a rotating magnetic field vector on any desired plane, simply by rotating the magnet about a unique axis-of-rotation [9]. This concept is illustrated in Fig. 2, where the rotating magnet is shown in three example configurations, each with a unique axis-of-rotation (Ω̂) to generate a magnetic field vector at the cochlea that rotates on the basal plane, about the modiolar axis. Thus, from any arbitrary position outside the patient’s head, the rotating MDS can generate the necessary rotating magnetic field for guided insertions. Note that in all the configurations shown, the direction from the MDS’s center to the cochlea does not change. This allows the magnet to rotate about a constant axis-of-rotation while translating toward or away from the patient’s head along a single degree-of-freedom. Part of the surgical planning could require the MDS to be positioned to some minimum clearance from the surface of the head with the linear stage extended to its maximum range of travel. Then, the linear stage could be retracted along the planned translation direction to the beginning of its range of motion. Such an alignment procedure would preclude any potential collision with the patient.
Fig. 2.
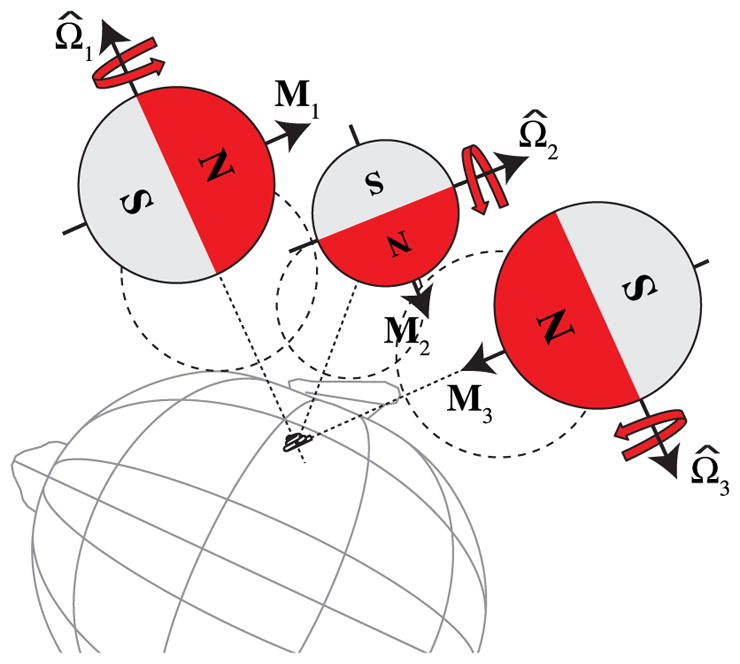
Three example configurations in which a spherical-permanent-magnet MDS translates relative to the patient’s cochlea along a straight trajectory while rotating about some fixed axis Ω̂. The trajectories are not aligned with the surface normals of the patient’s head, in general. The required size of the MDS will be determined by how close it can get to the cochlea without collision, which is depicted by the dashed circles. Note that configuration 1 corresponds to the modiolar configuration of Fig. 1(a).
In this paper, we explore the optimal configuration in which the smallest MDS needed to accomplish guided insertions is determined along with its location relative to the cochlea. Throughout the optimization process, we assume that the MDS is a spherical permanent magnet. Spherical magnets have the desirable property that the point-dipole model perfectly describes their magnetic field [10]. In addition, our group has already developed a robotic end-effector that comprises a spherical permanent magnet [11]. Alternatively, an electromagnetic source such as an Omnimagnet [12], whose magnetic field is accurately described by the point-dipole model outside of its minimum bounding sphere, could be used in place of a spherical permanent magnet. In that case, it would not be necessary to translate the MDS relative to the patient’s head to vary the field strength at the cochlea, because the strength of its magnetic dipole can be controlled directly. However, large currents will be necessary to generate the required dipole strength from an Omni-magnet of a given minimum bounding sphere compared to a spherical permanent magnet of the same size.
The outline of this paper is as follows. In Sec. 2, we present all of the necessary modeling equations that relate the size, strength, and location of the MDS to the magnetic field that can be generated at the cochlea. In Sec. 3, computed-tomography (CT) scans of 30 human subjects are segmented to create three-dimensional models of the surfaces of the subjects’ heads, along with the location and orientation of the cochlea. In Sec. 4, we determine the optimal configuration (size and location) of the MDS for each of the 30 subjects. We compare the results to the MDS required in the modiolar configuration and find that the MDS size can be substantially reduced by moving it to the optimal location. Although we are primarily relying on magnetic torque applied to the EAT to bend the electrode array, in general there will also be a magnetic force applied to the EAT. In Sec. 5, we provide a conservative force estimate that indicates that magnetic forces are unlikely to apply any forces that might be dangerous to the delicate basilar membrane. In Sec. 6, we perform a sensitivity analysis to the size, strength, and positioning of the MDS. Although we compute subject-specific optimal configurations in this paper, it is likely more practical to develop a one-size-fits-all MDS, which will be overdesigned for the majority of patients; in Sec. 7, we consider the robust placement of the MDS in light of this fact. In Sec. 8, we explain how to translate the optimization results to an Omnimagnet as the MDS. We conclude with a discussion of the practical application of our results in Sec. 9.
2. Magnetic Modeling
The necessary magnetic field to achieve successful guided electrode-array insertions has been determined by our prior work [8]. In that study, Flex-24 electrode arrays provided by MED-EL (Innsbruck, Austria) with a 4.73×10−5 A·m2 permanent magnet embedded in the EAT were guided successfully through a plastic scala-tympani phantom [7]. The maximum magnetic field used in those experiments was determined to be 80 mT and 100 mT if inserted through a simulated cochleostomy and round window, respectively. We will use 100 mT as the nominal magnetic-field requirement herein.
The magnitude of the dipole moment M, in units {A · m2}, for a spherical-permanent-magnet MDS of radius r in units {m} is given by
| (2) |
where μ0 = 4π ×10−7 T · m · A−1 is the permeability of free space and Br = μ0M̃ is the residual flux density in units {T}, where M̃ is the magnetization in units {A · m−1}. Br and M̃ are intrinsic properties of the permanent magnet [10].
The magnetic field vector B in units {T} that is generated at the cochlea by a spherical magnet, modeled as a dipole M, can be computed by the point-dipole equation
| (3) |
where p is the vector from the magnet’s center to the cochlea in units {m} [9]. We will define the location of the cochlea as the intersection of the modiolar axis and the basal plane [7].
We can simplify the use of (3) based on our intended use of the MDS. We intend to mount it on a one-degree-of-freedom linear stage with its linear trajectory preplanned so as to avoid any contact with the patient at any point during its translation. During initial positioning, we envision the MDS to be placed as close to the surface of the head as allowable. This will represent the point on the trajectory where the distance between the MDS and the cochlea is shortest, as illustrated by the dashed circles touching the head surface in Fig. 2. In general, the shorter the distance between the MDS and the cochlea, the smaller the MDS can be and still generate the needed magnetic field. Now suppose that at its closest approach to the patient, the MDS rotates about the required rotation axis Ω̂, with M orthogonal to Ω̂, in order to generate a rotating field vector that lies on the basal plane. For every complete revolution of M about Ω̂, the field magnitude will vary based on the relationship between M and p, and it will reach a minimum (whenever M ·p = 0) of [9]:
| (4) |
We are searching for the location where the MDS can be smallest, so we cannot know the trajectory of the MDS in advance nor the relationship between M and p. In addition, if we insert the EA deep enough, the MDS will have to undergo a complete rotation. Therefore, to be conservative we will assume that the field magnitude is always at this minimum possible for a given p.
Assuming that the field magnitude necessary to achieve guided insertions of electrode arrays are known [8], then combining (2) and (4) yields the equation to compute the required minimum radius of the MDS.
| (5) |
Taking each surface point on the head, we can simulate a spherical magnet touching the point and normal to the local surface as defined by the surface normal (see Fig. 3). By defining this surface point as s and its surface normal of unit length as n̂, the vector from the center of the magnet to the cochlea is
Fig. 3.
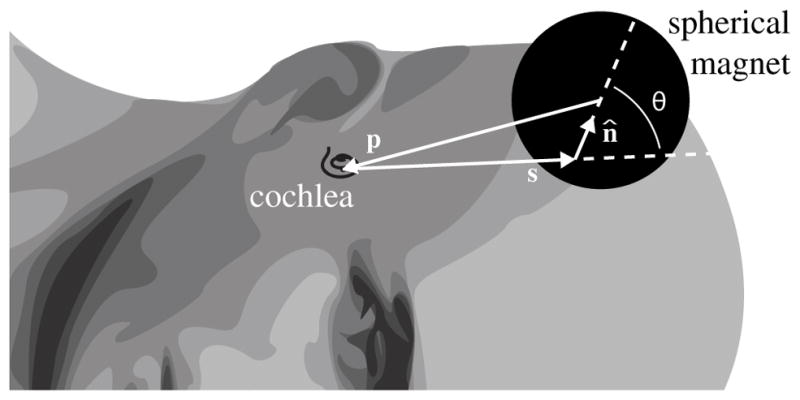
Vectors defining an arbitrary surface point s and its unit surface normal n̂ with respect to the cochlea. p is the vector from the center of the spherical magnet, which is touching the head at s, to the cochlea. θ is the angle between s and n̂.
| (6) |
where r is the radius of the magnet and δ is the clearance from the surface point to the surface of the magnet along n̂. In the case where the magnet touches the patient, the clearance is δ = 0.
The distance from the magnet center to the cochlea can be calculated using the (modified) law of cosines as
| (7) |
where sn = ||s|| cosθ and θ is illustrated in Fig. 3. sn can also be considered the projection of ||s|| onto n̂.
Next, we rearrange (5) into the following form:
| (8) |
where the nondimensional term
| (9) |
expresses a ratio of the required magnetic field (||B||min) to a magnetic property of the material (Br). By combining (7) with (8) and rearranging it into the form of a quadratic equation
| (10) |
r required at some surface point s can be solved for using the quadratic formula. The standard quadratic formula yields two solutions, and the solutions are not guaranteed to be real. Fortunately, we can constrain some of the parameters, based on our application, to yield a valid solution to (10) (i.e. r ∈ ℝ+): K > 0, ||s|| > 0, and δ ≥ 0.
We ignore all surface points with surface normals directed back toward the cochlea by selecting only the surface points in which s · n̂ ≥ 0 (i.e. sn ≥ 0). This typically eliminates some of the points on the ear or nose as shown in Fig. 4.
Fig. 4.
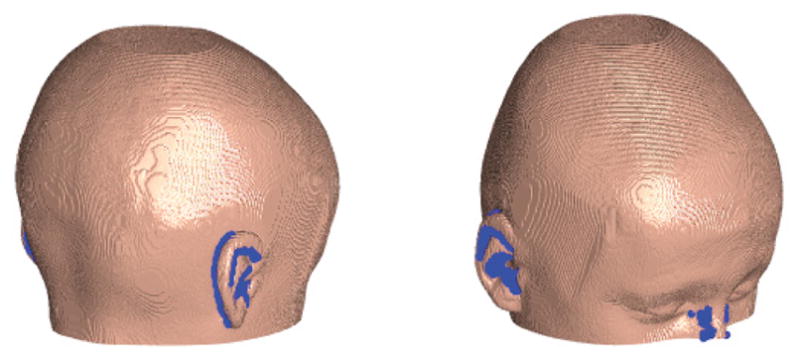
Surface rendering of a subject, with blue points indicating where s · n̂ < 0 are excluded from the analysis.
Finally, by further restricting 0 < K < 1, the solution to (10) always yields r ∈ ℝ+ and is given by
| (11) |
The constraint on K implies that the required magnetic field strength at the cochlea must not be more than the residual flux density of the magnet.
| (12) |
Since the field measured on the surface of a spherical magnet falls within the range , (12) represents a conservative estimate of the field that can be generated by a spherical magnet in an arbitrary direction p̂.
3. Segmentation of CT Scans
Using (11) to compute the magnet size required at a given location relative to the patient’s head requires a set of surface points and their associated surface normals. To our knowledge, a representative head-surface model of sufficient fidelity has not been published in which the location of the cochlea is also identified. In practice, patient-specific head surfaces can be generated from standard, preoperative CT scans. In this section, we describe a generalized image-processing pipeline that we employed; we also provide the specific MATLAB commands used in Table A.1 in the appendix. The process yields a three-dimensional map of surface points and their surface normals for our analysis.
CT scans of 28 anonymous subjects were obtained from the University of Utah. Standard CT temporal-bone imaging procedures were used in each case. In addition, two sets of cadaver scans were obtained from the National Library of Medicine’s Visible Human Project [13]. In all sets, the pixel resolution is less than 1 mm, but the slice resolution varied significantly from set to set. Data describing the gender and age of the 30 subjects, as well as the resolution of the CT scans, is provided in Table A.2 in the appendix. The CT data is available as DICOM binary data and packaged as 12-bit grayscale image intensity values and a header with meta-data regarding the CT scan and the imaging protocol used. The meta-data is needed to convert from image frame to the CT frame. We use the standard right-anterior-superior (RAS) convention in which +x is directed to the subject’s right side, +y is directed anteriorly, and +z is directed superiorly.
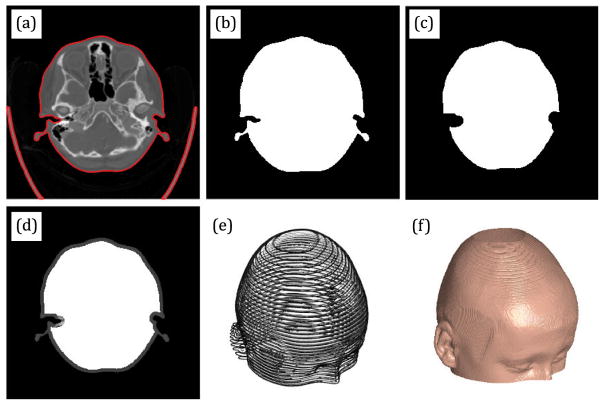
All grayscale images are converted to black-and-white where the threshold to determine if the pixel should be considered black or white is set automatically by Otsu’s method. Each slice of each set is then segmented to extract the boundary of the skull. We show an example of automatically generated boundaries, in red, overlayed on the grayscale image in Fig. 5(a).
Fig. 5.
Illustration of the main segmentation steps.
The skull boundary is used to build a slice-specific image mask to remove all features outside this mask (Fig. 5(b)). The mask is a logical array where all locations inside the mask are set to true and all locations outside the mask are set to false. This mask can be visualized by mapping false and true to black and white, respectively. To remove the background, all pixels of the grayscale image that are outside this mask will have their intensity values set to zero, yielding an image of just the head without the background.
Next, this image mask is eroded (i.e. made smaller) for the purpose of handling internal features of the head, such as the nasal cavity (Fig. 5(c)). This is necessary because these features could be interpreted as part of the head surface. To handle this, we set all the intensity values for all the pixels inside this eroded mask to the maximum intensity value of the image slice.
The result is an image where the background is removed and the interior features are washed out, with a thin border of grayscale pixels at the head surface (Fig. 5(d)). The resulting segmented images are then stacked to create a three-dimensional array of intensity values per pixel and slice. This is illustrated in Fig. 5(e) (but only showing every tenth slice). This array of intensity values can also be regarded as a scalar function of three parameters I = f (x, y, z), where x and y are the pixel coordinates, z is the slice coordinate, and I is the scalar intensity value at those coordinates. As a result, this function can be interpolated to find the coordinate (x, y, z), where the intensity map transitions away from the background intensity. Interpolation then yields the approximate coordinates of the head surface, and this can be accomplished through the following steps. First, a homogenous transform is used to convert the pixel and slice coordinates from the image frame to the global CT frame. Then, the scalar function is filtered to generate smoother surface normals. Next, we interpolate for the coordinates at the desired intensity value. We chose an intensity value of 5 as representative of the transition from the background to the head surface (the images are provided as 12-bit unsigned integers, where 0 is mapped to black and 4095 is mapped to white). Finally, the surface normals corresponding to the surface points interpolated are generated. The combination of surface points and surface normals define the final head surface, as illustrated in Fig. 5(f). This pipeline is adapted from tutorials provided by Mathworks (Natick, MA) [14] for producing three-dimensional surfaces from medical images.
Finally, the location of the cochlea (as defined in Sec. 2) is determined for both sides of each subject (Fig. 6). In one study [15], the average angle between the modiolar axis and the transverse plane of the skull was determined to be nearly zero (1.8° ± 3°, n = 10). So, for simplicity, we will assume that the modiolar axis lies on the slice plane, where the cochlea is located. We examined each CT set to ensure the cochlea could be visualized in at least three of the slices. All sets summarized in Table A.2 of the appendix satisfied this criteria. Next, we chose to examine the slice with the largest cochlear footprint. This may yield a potential error of 1 slice along the inferior-to-superior coordinate. A line is then drawn through the basal chamber of the cochlea. A second line is drawn to estimate the central spiral axis (which we considered to be the modiolar axis). The intersection of these two lines at the chosen slice is considered to be the location of the cochlea. This visual approximation may yield an error of 2 to 3 pixels within the transverse plane of the subject, and we estimate a maximum localization error of 5 mm, largely due to the slice thickness. This method is imprecise compared with the automated algorithms [16] that would be used during surgical planning. However, in our opinion, this resolution is sufficient for the analysis in this paper given that the results are more sensitive to other factors as will be shown in Sec. 6, in which we include this localization uncertainty by treating it as an MDS registration error. Ultimately, the full pose of the basal plane is important for our magnetic-guidance approach because we want to apply the magnetic field in this plane, but it is not as important for the optimization described herein since (11) is independent of Ω̂.
Fig. 6.

The location of the cochlea and the modiolar axis.
An alternative method for computing the surface normals was attempted on the boundary points directly (Fig. 5(a)) so as to avoid the steps after boundary segmentation, but we found the surface normals to be more noisy and settled on the method described above. However, the possibility of noisy surface normals motivated an alternative method, independent of surface normals, to verify the results computed by (11); this is described in Sec. 4.1.3.
4. Determining the Optimal Configuration
4.1. Methods
4.1.1. Using surface normals
For each surface point obtained from the segmentation, and that satisfy s ·n̂ ≥ 0, the MDS radius r is computed by (11). To ensure that this MDS does not collide with any point on the head surface, the corresponding p is computed using (6), assuming δ = 0. If ||p + s|| ≥ r is true over the entire set of all surface points s, no collision occurs, and this configuration is valid. The valid surface point that yields the smallest r is considered optimal. The corresponding p determines its optimal placement relative to the cochlea.
4.1.2. On the modiolus
For comparison, we also determine the smallest MDS allowable if it is constrained to be on the modiolar axis, as in our prior work. Points are sampled on the modiolar axis at increments of 0.1 mm and represent the set of hypothetical locations for the MDS. At each sampled point, the smallest MDS (of radius r with δ = 0) needed to generate the required magnetic field is computed using (5), where ||p|| is simply the distance from the sampled point to the cochlea. The last step is to perform collision detection at each sampled point to determine if the MDS will collide with any of the surface points on the head. If there are no collisions, then the sampled point is valid. The same condition is applied for collision detection as in Sec. 4.1.1. The valid point yielding the smallest radius is the smallest MDS allowable for the modiolar configuration.
4.1.3. Using brute force
To verify the results computed by (11), an alternative method that is independent of surface normals is also conducted. The method is identical to that described in Sec. 4.1.2, except that the entire space exterior to the head is uniformly sampled at the resolution of the subject-specific CT scan. Thus, for each sampled point, there will be an associated radius r that represents the smallest MDS required to generate ||B||min at the cochlea if the MDS were centered at that sampled point. The optimal configuration using this method is the sampled point that yields the smallest r without any collisions.
4.2. Results
4.2.1. Using surface normals
The compiled results over the entire data set of subjects is presented in Table A.3 in the appendix. The optimal location is identified by the distance ||p|| and the direction from the cochlea to the MDS center. The direction can be expressed compactly by the unit vector −p̂; recall that p̂ is the unit vector in the opposite direction (i.e. from the MDS center to the cochlea). All unit vectors assume the RAS convention. Since the optimal MDS location is associated with a surface point, this is also provided as a distance (||s||) and direction (ŝ) from the cochlea. The angle between this surface point and its surface normal (θ) is also listed. r and rm are the computed radii at the optimal and modiolar configurations, respectively. At the bottom of Table A.3 are some basic statistics for the entire set.
Across all the subjects analyzed, there is a 19 mm range in the radii of the optimal MDS (55.0–73.5 mm). There is a 32 mm range in the distances from the cochlea to the MDS center (93.3–125 mm); this is the most variable of the parameters listed.
The optimal MDS placement is mostly lateral-to and slightly anterior-to the cochlea. This is a fortuitous result because the typical approach to the cochlea requires an incision behind the ear [17], making it impractical to position the MDS behind the ear. Our results indicate that the optimal configuration will not interfere with the surgical insertion. There does not seem to be a clear trend for the z-coordinate of the MDS as there seems to be a balance in the instances, where the MDS should be placed superior to or inferior to the cochlea. The direction to the optimal surface point tends to be more anterior than the direction to the MDS center.
4.2.2. On the modiolus
By moving the MDS away from the modiolar configuration, its size can be significantly reduced. For example, in the case of P28 shown in Fig. 7, the radius is reduced by half, resulting in an eight-fold decrease in the volume. On average, over our entire 30-subject data set, the radius is reduced by approximately 43% (see Table A.3), yielding an approximately five-fold decrease in the volume of the magnetic sphere on average. Also, the range and standard deviation in radius values are cut approximately in half in the optimal configuration. There is variability in the side-to-side optimal results within each individual, but in the aggregate the left and right values were very similar. If we consider only the maximum radii found over our entire 30-subject data set, as we might in the design of a one-size-fits-all system, we find that the radius computed in the modiolar configuration is 80% larger than it needs to be (132 mm versus 73.5 mm).
Fig. 7.
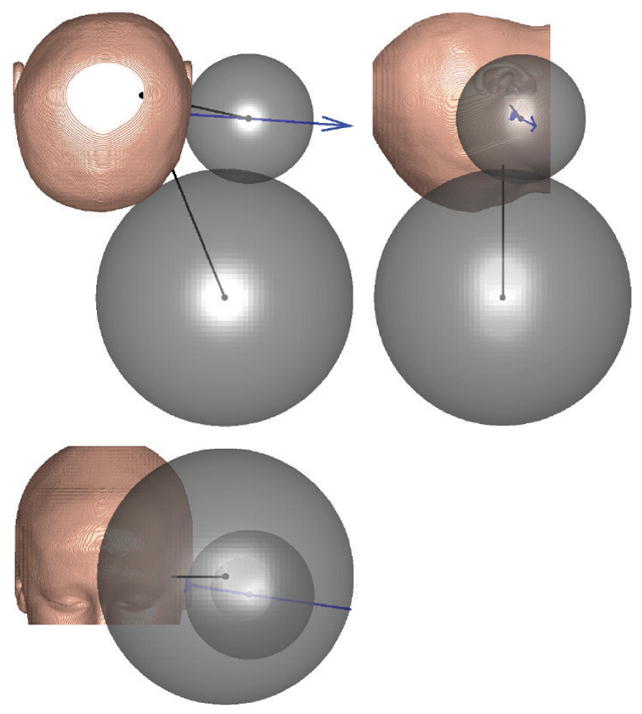
Three orthogonal views of a single subject showing how the size of the MDS is drastically reduced by moving it away from the modiolar axis (large MDS) to the optimal configuration (small MDS). Black lines are drawn from each of the MDS centers to the cochlea (which are all shown with black dots). The spatial location of the cochlea can be visualized as the intersection of these two black lines in each view (and can be seen directly in the upper-left view). A blue arrow indicates the surface normal at the optimal surface point (which is shown with a blue dot). These results are typical of all human subjects.
4.2.3. Using brute force
A table of results for the brute-force method, similar to Table A.3, is provided in Table A.4 in the appendix. With the exception of a few cases, the brute-force search method yielded slightly smaller radii values than the surface-normals method. On the aggregate, however, the surface-normals method yields an average radius of only about 1 mm larger, making it slightly conservative and thus better for our purpose. The main drawback to the brute-force method is that computation times are considerably longer because it typically yields approximately 1000 times more points to examine than the surface-normals method.
5. Magnetic Force
In all prior work, the MDS used to generate the magnetic field at the cochlea was assumed to be in the modiolar configuration. One benefit of this configuration is that the magnetic force that could potentially attract the EAT into the basilar membrane was negligible and could be disregarded during the insertion [6]. However, at the optimal configuration, this assumption should be verified since avoiding trauma to the basilar membrane is widely considered vital for hearing preservation [4]. The threshold for puncturing the basilar membrane has been measured to be approximately 42 mN [18]. We compute the worst case and assume that the entire force vector is directed into the basilar membrane. While this is not accurate, it does present a conservative upper bound.
The magnetic force applied to the tip is given by
| (13) |
where B is computed by (3) and m is the dipole moment of the EAT. For a given ||p||, the largest magnitude and spatial derivative of the field vector occurs along the dipole axis of M (i.e. where M and p are parallel). The maximum possible force magnitude at a given ||p|| is therefore computed by differentiating ||B|| with respect to ||p||, with M parallel to p, yielding
| (14) |
As a nominal value for ||m||, we will use the magnets embedded in the EAT in our prior work [8] which has been determined to be 4.73 × 10−5 A · m2. This represents the combined magnetic dipole for two 0.41-mm-long by 0.25-mm-diameter cylindrical magnets made of grade N52 NdFeB.
At the optimal position, for all subjects and sides examined, the maximum magnetic force possible never exceeded 0.31 mN, with an average and standard deviation of 0.267 mN and 0.019 mN, respectively. For comparison, we also compute the maximum magnetic force possible if the MDS were positioned at the modiolar configuration for each subject and found that the average and standard deviation is 0.150 mN and 0.012 mN, respectively. Note that by moving the MDS from the modiolar configuration to the optimal configuration, the maximum possible magnetic force averaged over the set is increased by nearly 80%. In context however, the force is still over 100 times smaller than what is needed to puncture the basilar membrane. Therefore, it seems reasonable to state that any additional magnetic force that may pull the EAT into the basilar membrane arising from the MDS being moved to the optimal configuration does not truly pose any appreciable risk to the basilar membrane.
6. Sensitivity Analysis
Achieving the optimal configuration requires perfect registration of the MDS with respect to the cochlea, and hardware implementations will have practical design constraints. A sensitivity analysis to registration, magnetic material properties, and any clearance requirements between the MDS and the patient would be useful. This is motivated by the reality that these factors may reduce the magnetic field generated at the cochlea and thereby limit the amount of insertion-force reduction that can be achieved with magnetically guided insertions.
For each parameter of interest, using (11), r can be solved for over the possible range of the parameter while fixing the remainder of the inputs to their nominal values. With this in mind, in this section, we first provide the nominal values used by the search method, as well as the range of expected values for those parameters. We conclude with plots that show the sensitivity of r to the input parameters within the range defined. These plots are provided to enable readers to get a quick sense of the how the optimal MDS can vary as a function of the various parameters. However, we do not recommend using these plots in a formal design; rather, the equations in Sec. 2 should be used directly.
The nominal value for Br is 1.465 T, which corresponds to a NdFeB magnet of grade N52. This is the highest grade of magnetic material available, and it is what one would likely choose. The range of values for grade N35–N52 is 1.19–1.465 T [19]. We chose to use a nominal value of 100 mT for the required magnetic field strength ||B||min. For the range of ||B||min, we will explore 80–120 mT, representing a 20% variation in that parameter.
The nominal value for the gap (δ) was set to zero and describes the situation where the spherical magnet just touches the head. However, the spherical magnet itself will likely be contained in a housing. An existing MDS in our lab, using a 50-mm-diameter N42 NdFeB sphere, has been designed with a 7-mm-thick housing [11]. So, if this MDS were to be used, then δ = 7 mm, assuming the housing of the MDS touches the head. We will use a range of values from 0–25 mm for δ to conduct the sensitivity analysis.
In our context, registration error can broadly be considered as the position error in the initial placement of the MDS center, relative to the cochlea. This error can be due to either misplacement of the MDS, or incorrectly estimating the location of the cochlea. We believe the contribution from errors in locating the cochlea will be negligible since Bell et al. [20] have already demonstrated successful automated insertions in temporal bones to sub-mm accuracy based on CT localization of the cochlea. For this reason, sensitivity to registration can be assessed by evaluating the effect on r due to error in ||p|| as indicated by (5). Although the optimal results found in Table A.3 were computed using (11), which utilized the surface normal, r is most sensitive to distance changes along p̂, which makes consideration of error along p̂ a conservative bound on registration error in any direction by the same amount. In Fig. 8, r is computed based on the change from the optimal ||p|| for each human subject (Table A.3) over the range of ±10 mm. The results for each subject and each side are plotted together on a single graph, assuming the nominal value of ||B||min and Br.
Fig. 8.
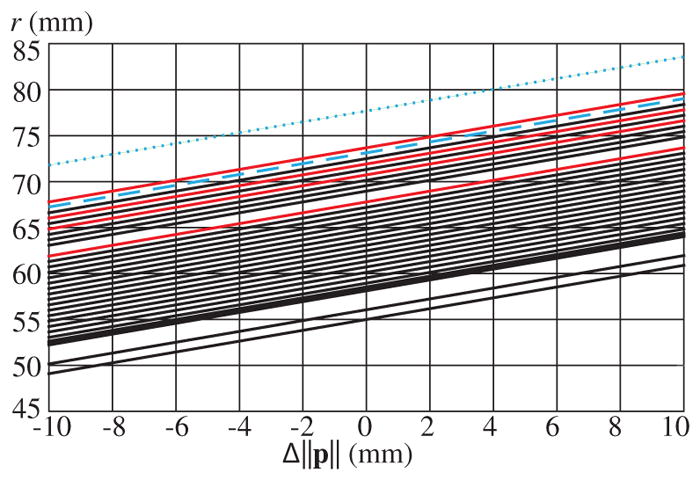
r as a function of Δ||p|| for all subjects analyzed. C1 and C2 results are shown in red, with all others shown in black. The blue-dashed and blue-dotted lines indicate two and three standard deviations above the mean, respectively.
Sensitivity results pertaining to the MDS hardware design are grouped into two categories. The first category represents the effect from the magnetic field desired and the magnetic property of the MDS, as expressed by the nondimensional parameter K. In Fig. 9(a), we display K over the range of ||B|| outlined earlier (i.e. 80–120 mT) and the range of magnetic grades commercially available. This range of K is then used to compute the values of r in Fig. 9(b). This is computed for each subject and each side separately and plotted together on a single graph. We assume the nominal value of δ, ||s||, and θ for these results.
Fig. 9.
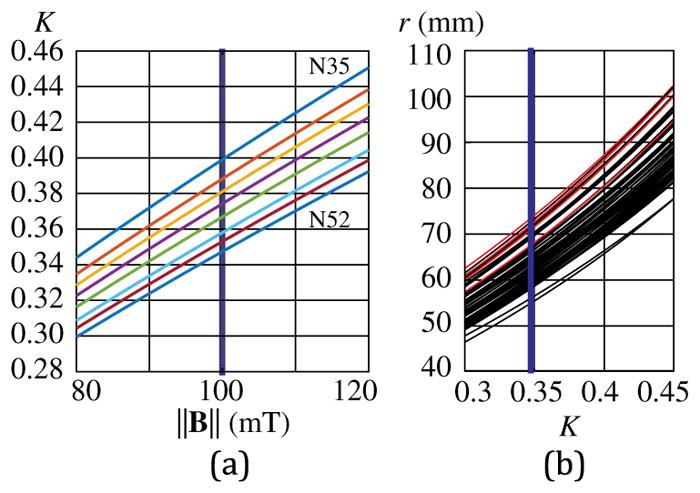
(a) Expected range of K given the range of ||B|| considered, for commercially available permanent-magnet grades of the MDS. The blue vertical line is the nominal value for ||B||, and N52 is the nominal grade. The resulting range of K is used in (b), which shows r as a function of K for all subjects analyzed. C1 and C2 results are shown in red, with all others shown in black. The blue vertical line is the nominal value for K, which is the intersection of ||B|| 100 mT and N52.
The second category represents the effect from increasing the clearance between the magnet and the surface of the subject. In Fig. 10, r is computed as a function of δ over the range defined earlier (i.e. 0–25 mm). This is also computed for each subject and each side separately and plotted together on a single graph. We assume the nominal value of K, ||s||, and θ for these results.
Fig. 10.
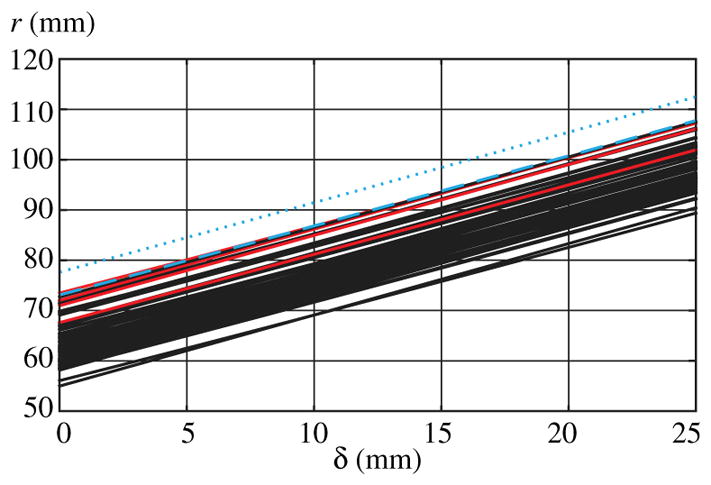
r as a function of δ for all subjects analyzed. C1 and C2 results are shown in red, with all others shown in black. The blue-dashed and blue-dotted lines indicate two and three standard deviations from the mean, respectively. The two-standard-deviation line is approximately aligned with the largest result from our human subjects.
In Figs. 8, 9(b), and 10, we chose to present the 60 individual subject-side curves, rather than showing only aggregate statistics. This choice enables the reader to visualize the difference in r, as a function of the respective parameters, for the largest and smallest human subjects in our study, as well as the distribution generally.
7. Oversized MDS
We now consider the design of a one-size-fits-all MDS for magnetically guided insertions. In order to generate the necessary magnetic field across as many patients as needed, the MDS will be needed to be oversized for the vast majority of patients. As a result, a one-size-fits-all MDS will not need to get equally close to all patients’ heads during the closest approach (i.e. at the point of maximum field generation).
To gain some insight into this, we choose a 75-mm-radius MDS; this is only about 1.5 mm larger than the maximum value for r listed in Table A.3. All the valid locations generated by the brute-force method for each subject and each side are identified for the oversized MDS. Recall that valid locations are those in which two constraints must be satisfied. First, the MDS centered at this location must be able to generate the required magnetic field at the cochlea. Second, the MDS must not collide with any part of the subject’s head at this location. Let us define the point cloud that contains all the valid points that are also anterior to the cochlea. We can compute the centroid of this point cloud, v, by averaging these valid points; the results are presented in Table A.5 of the appendix. Attempting to place the MDS at the centroid will yield a location that is robust (i.e. insensitive) to registration and other errors.
An example using P28 is provided in Fig. 11, where every point represents a valid location of the 75 mm oversized MDS in its closest approach to the subject’s head. All points that are posterior to the cochlea are shown in red; all points anterior to the cochlea are shown in black. Since the optimal radius for P28 is approximately 59 mm, an MDS whose radius is 75 mm represents a 28% increase in the radius over what is needed. This yields many valid points at which the MDS can be located. In practice, it is best to ignore all the locations that are posterior to the cochlea because the insertion is conducted behind the ear, and placing an MDS anywhere behind the ear is impractical. Further, potential points superior and inferior to the top-most and bottom-most CT slice are ignored since there is no sufficient surface data available for collision detection.
Fig. 11.
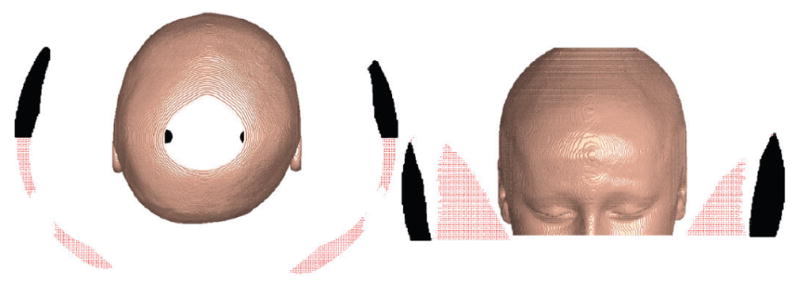
All valid locations to place an MDS that has been oversized to 75 mm radius, for P28. Black points are anterior to the cochlea. Red points are posterior to the cochlea. The black dots inside the head (left) locate the cochleae.
In general, the shape of the point cloud also suggests more robustness along the y- and z-directions as compared to the x-direction. In principle, this should not be a problem because the initial alignment of the MDS requires the edge of the MDS to contact the surface of the head. This physical constraint will help enforce the tighter tolerance needed in the x-direction.
8. Electromagnetic MDS
Until this point, we have exclusively considered a spherical permanent magnet as the MDS, due to both the simplicity in modeling the field generated by a spherical permanent magnet, as well as the simplicity of its geometry for collision detection. However, it may be desirable to use an electromagnetic source as the MDS for three reasons: First, an electromagnet has a controllable magnetic dipole, which means that it does not need to be actively translated during the insertion to vary the field strength at the cochlea. Second, an electromagnet can be turned off, making it inert when not in use; a strong permanent magnet represents an ongoing safety concern. Third, the relatively short duration of an electrode-array insertion (typically less than 30 sec) would allow high levels of current to be sourced through the coils without reaching unsafe temperatures.
Our group previously developed an electromagnetic source that was explicitly optimized to be modeled as a magnetic point-dipole source: the Omnimagnet [12]. The Omnimagnet comprises three nested mutually orthogonal coils, with a spherical ferromagnetic core at the common center. The geometries of the individual coils and the size of the spherical core were parametrically optimized to fit within a cubic bounding volume of side-length L (in units {m}) while achieving the following specifications: First, the dipole strength in each of the three orthogonal basis directions is the same given the same current density J (in units {A · m−2}) in each coil. Second, the second-largest term in the multipole expansion after the dipole field, which is called the quadrupole field, is zero in all three basis directions to ensure that the dipole-field model accurately approximates the Omnimagnet’s field at close distances. The strength of the dipole field decays as ||p||−3, the quadrupole field decays as ||p||−5, and the remaining terms in the multi-pole expansion decay as ||p||−7, ||p||−9, etc. Third, the Omnimagnet has as strong a dipole as possible for a given current density in the coils.
The field of an Omnimagnet can be approximated by the point-dipole model (3) outside of its minimum bounding sphere (which touches the corners of the cube and has a radius of ), and is accurate to less than 5% error at all points outside of 1.5 minimum-bounding-sphere radii [12]. The dipole moment of an Omnimagnet is ||M|| = 0.051L4J [12]. In any actual engineered Omnimagnet, there will be limits on the current density J that can be sourced through the coils due to the power supply and amplifiers chosen as well as safe heating limits. At this maximum J, the Omnimagnet’s dipole strength will be at its maximum, and we can use this maximum dipole strength to make a direct analogy to the spherical-permanent-magnet dipole strength that we have used throughout the development in this paper. We can use whatever bounding-sphere radii we choose to achieve a given level of accuracy, which will change the effective values of M̃ and Br that are distributed over the effective spherical volume. This method will tend to be conservative, since the patient’s head could have been allowed to partially reside inside of the bounding sphere while still avoiding collision with the Omnimagnet.
9. Discussion
In this paper, we have rigorously described the process by which anyone could determine, on their own, the minimum MDS size and its location for a given patient, and for a given EAT magnet strength and required torque. For a device maker interested in building an MDS to accommodate the general population, it might be worthwhile to obtain a larger number of head surfaces (particularly of large heads) to supplement the data set examined here. For this purpose, our data set of rendered surface points and surface normals is available upon request by contacting the corresponding author. Our description of a 75 mm MDS in Sec. 7 should not be construed as a recommendation of the optimal one-size-fits-all size. First, the dimension was arbitrarily chosen to slightly exceed the maximum r in Table A.3. It may be more desirable to specify a size from an average and standard deviation based on this study or a larger population study. Second, the results in Sec. 7 assumed no clearance between the head surface and the magnet (i.e. δ = 0) and assumed the nominal value of K. In practice, the available magnetic grade (see Fig. 9) and the designed housing thickness (see Fig. 10) will drastically impact the size of a permanent-magnet MDS, and the allowable current density will drastically impact the size of an electromagnetic MDS. Third, we have determined in our prior work [8] that the required magnetic field can vary substantially based on electrode-array models. Therefore, it may even be necessary to have electrode-array specific MDS models as well. Even the progress toward thinner and more flexible electrode arrays may yield a smaller MDS in the future. Fortunately, these electrode-array specific variations, whether magnetic or mechanical, can be handled by determining their effect on the required magnetic field ||B|| (see Fig. 9). Finally, a specific registration tolerance might be preferred by the clinicians and would require an analysis similar to that done for Fig. 8. Under these various circumstances, the device maker can either conduct a full optimal configuration analysis (Sec. 4) or use the sensitivity curves in Sec. 6 for their MDS design.
The magnetic guidance strategy works best if both the lumen and modiolar axis are determined for each patient. Fortunately, it is standard practice to include a CT-based radiological assessment as part of the complete preoperative medical assessment for cochlear-implant candidacy. There is little reason for not planning patient-specific magnetically guided insertions given the ease in which cochlea segmentation can be done [16]. Further, since software can be implemented to generate a patient-specific head surface (as described in Sec. 3), the method outlined in Sec. 7 can be used to determine a patient-specific centroid location for a one-size-fits-all MDS that is most robust to registration error. Although our work describes this centroid with respect to the cochlea, it can be expressed relative to external markers on the patient (e.g. bone anchors [21]). In such a scenario, an optical tracker could register the MDS to the centroid location with high accuracy [22].
In traditional ear surgery, a large retractor is used to reflect the ear forward so that the surgeon can look inside the area with a microscope. It is possible that this could interfere with the MDS placement, particularly in the case of the spherical-permanent-magnet MDS; the cubic Omnimagnet can be rotated to mitigate interference. However, since the MDS is intended to be used with an automated electrode-insertion tool, the retractor could be removed since visualizing the facial recess is unnecessary to accomplish automated electrode insertions.
Standard temporal-bone CT protocols start the scan below the mastoid process and end just above the petrous ridge [23]. This effectively yields data sufficient only to render the middle portion of the head, typically including the eyes and nose. With the exception of P28, all CT scans of the subjects were done this way. Only the cadaver scans (C1 and C2) included the section below the nose to the shoulder. Fortunately, the optimal magnet size and location likely would not change with more slices. This can be seen in Fig. 12, where we show contour maps of distances from the cochlea to the surface points for C1 and C2, as well as for one standard-protocol subject (P25); in addition, the point where the optimal MDS touches the surface is indicated by a large blue dot. The smallest possible magnet will be located, where the distance is shortest to the cochlea, barring collision with the head, and it is clear that using additional CT data will not find a global optimal that is different than the local optimal found using the standard-protocol data.
Fig. 12.
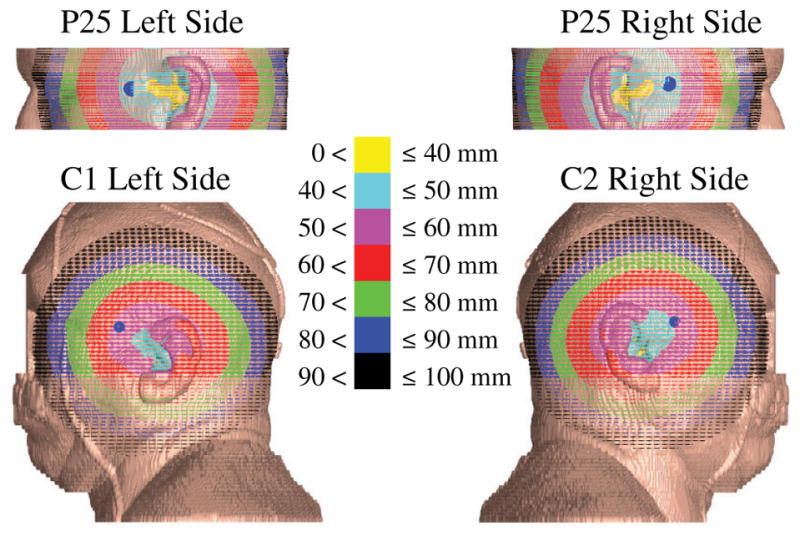
Contour map of ||s|| for P25 and C1. Blue dots indicate where the optimal MDS touches the surface of the head.
10. Conclusion
We described a method to determine the patient-specific configuration (size and location) of a spherical-permanent-magnet dipole-field source for magnetically guided cochlear-implant electrode-array insertions, using standard CT temporal bone scans. To generate 100 mT at the cochlea, the optimal configuration of the dipole-field source should be lateral-to and slightly anterior-to the cochlea with an approximate radius (mean and standard deviation across subjects) of 64 mm and 4.5 mm, respectively. When compared to the configuration assumed in prior work, the optimal location yields a 43% reduction in the dipole-field source’s radius and a nearly five-fold reduction in its volume. Although potential magnetic forces that may direct the tip into the basilar membrane are increased by nearly 80% at the optimal configuration compared to the modiolar configuration, they are still two orders of magnitude below the threshold needed to puncture the membrane. Sensitivity curves were generated for the minimum radius at the optimal configuration and demonstrate that the optimization is most sensitive to the magnetic field requirement. A one-size-fits-all configuration with a dipole-field source of approximately 75 mm will yield a solution that is robust to registration error.
Acknowledgments
The authors would like to thank those that provided the data sets used to render the head shapes for this study: Richard H. Wiggins, III, M. D. from the University of Utah’s Department of Radiology and Imaging Sciences for providing the anonymous CT patient scans, and the U. S. National Library of Medicine (National Institutes of Health) for providing access to the Visible Human Project. We also acknowledge the University of Utah’s Center for High Performance Computing for providing computing resources.
Research reported in this publication was supported by the National Institute on Deafness and Other Communication Disorders of the National Institutes of Health under Award Number R01DC013168. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Biographies

Lisandro Leon received his B. S. and M. S. degrees from the University of Southern California, USA, both in Mechanical Engineering, in 1994 and 1998, respectively. He then worked in the defense industry on various topics including unmanned aircraft, satellites, lasers, optics, and tracking systems. He received his Ph.D. degree in Mechanical Engineering (Robotics Track) from the University of Utah, USA, in 2017. He is now with Sarcos Robotics, USA.

Frank M. Warren received his B. S. degree in biology from Tufts University, USA, in 1992, and his M. D. degree from Oregon Health and Science University, USA, in 1999. His research interests include applications of new technology to the practice of neurotology and radiologic imaging of the skull base. He is currently involved in research to develop a steerable cochlear-implant electrode array to improve cochlear implantation. Dr. Warren is a member of the American Academy of Otolaryngology and the American Neurotology Society.

Jake J. Abbott received his B. S. degree from Utah State University, USA, his M. S. degree from the University of Utah, USA, and his Ph.D. degree from Johns Hopkins University, USA, all in Mechanical Engineering, in 1999, 2001, and 2006, respectively. He was a Postdoctoral Researcher at ETH Zurich, Switzerland until 2008, when he joined the faculty of the Department of Mechanical Engineering, University of Utah, USA, where he is now an Associate Professor. His research interests include magnetic manipulation and telerobotic systems.
Appendix A. Tabular Data
In this appendix, we provide tabulated information used and data obtained in this paper. Table A.1 provides the MATLAB commands used in the image-processing steps of Sec. 3. Table A.2 provides information related to the 30 human-subject CT scans used in Sec. 3. Table A.3 describes the optimal size and placement of the MDS for each human subject, as well as the aggregate statistics, obtained in Sec. 4.2.1. It also includes the results for the modiolar configuration, obtained in Sec. 4.2.2. Table A.4 shows analogous results using the brute-force approach of Sec. 4.2.3. Table A.5 shows the location of a 75-mm-radius one-size-fits-all MDS, optimized for each human subject to be robust to registration errors, obtained in Sec. 7.
Table A.1.
MATLAB commands used in the image-processing steps described in Sec. 3.
| Image-Processing Step | MATLAB Command |
|---|---|
| Convert DICOM data | dicomread and dicominfo |
| Black-and-white conversion | im2bw and graythresh |
| Skull boundary segmentation | bwboundaries or bwtraceboudaries |
| Skull boundary mask | poly2mask |
| Eroded mask | imerode |
| Filtering | smooth3 |
| Surface interpolation | isosurface |
| Surface normals | isonormals |
Table A.2.
Database of human-subject CT scans. P1–P28 are scans of anonymous subjects provided by the University of Utah (UU). C1–C2 are scans of cadavers obtained from the National Library of Medicine (NLM).
| ID | Gender (M/F) | Age (yrs) | Source | Resolution (mm)
|
Total Slices | |
|---|---|---|---|---|---|---|
| Pixel | Slice | |||||
| P1 | F | 62 | UU | 0.41 | 0.6 | 89 |
| P2 | F | 52 | UU | 0.41 | 2 | 39 |
| P3 | F | 33 | UU | 0.41 | 2 | 37 |
| P4 | F | 60 | UU | 0.41 | 2 | 37 |
| P5 | M | 26 | UU | 0.44 | 5 | 16 |
| P6 | F | 42 | UU | 0.41 | 2 | 30 |
| P7 | F | 85 | UU | 0.41 | 4 | 16 |
| P8 | F | 21 | UU | 0.39 | 5 | 15 |
| P9 | F | 32 | UU | 0.41 | 5 | 15 |
| P10 | F | 65 | UU | 0.47 | 0.6 | 115 |
| P11 | F | 39 | UU | 0.49 | 3 | 23 |
| P12 | M | 48 | UU | 0.44 | 2 | 39 |
| P13 | F | 51 | UU | 0.43 | 1 | 68 |
| P14 | M | 64 | UU | 0.46 | 5 | 17 |
| P15 | F | 47 | UU | 0.34 | 2 | 25 |
| P16 | M | 79 | UU | 0.59 | 2 | 36 |
| P17 | F | 48 | UU | 0.43 | 2 | 33 |
| P18 | F | 52 | UU | 0.33 | 0.7 | 82 |
| P19 | F | 29 | UU | 0.57 | 2 | 32 |
| P20 | F | 39 | UU | 0.41 | 2 | 31 |
| P21 | F | 37 | UU | 0.59 | 2 | 36 |
| P22 | F | 36 | UU | 0.38 | 5 | 12 |
| P23 | F | 60 | UU | 0.41 | 0.6 | 98 |
| P24 | M | 36 | UU | 0.46 | 2 | 31 |
| P25 | F | 67 | UU | 0.39 | 1 | 78 |
| P26 | M | 83 | UU | 0.41 | 1 | 47 |
| P27 | F | 44 | UU | 0.32 | 2 | 31 |
| P28 | M | 8 | UU | 0.45 | 1 | 161 |
| C1 | M | — | NLM | 0.79 | 1.45 | 183 |
| C2 | F | — | NLM | 0.54 | 1 | 249 |
Table A.3.
Optimal configuration of the MDS as defined by its radius (r) and location relative to the cochlea (p). Vectors are expressed in the RAS convention, where +x is directed to the person’s right side, +y is directed anteriorly, and +z is directed superiorly. The MDS radius at the modiolar configuration (rm) is provided for comparison. Units are in {mm} except for θ in degrees and the unitless direction vector from the cochlea toward the MDS center. The optimal surface point associated with the optimal MDS configuration is defined by s.
| ID | Left Side |
Right Side |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||p|| |
|
||s|| |
|
θ | r | rm | ||p|| |
|
||s|| |
|
θ | r | rm | ||||
| P1 | 101 | [−0.95 0.31 −0.10] | 46.5 | [−0.78 0.59 −0.22] | 35.7 | 59.6 | 109 | 106 | [0.92 0.31 −0.22] | 52.3 | [0.70 0.68 −0.23] | 45.5 | 62.4 | 102 | |||
| P2 | 117 | [−0.91 0.38 −0.15] | 50.2 | [−0.80 0.56 −0.21] | 21.7 | 69.1 | 94.1 | 114 | [0.94 0.30 0.15] | 51.1 | [0.80 0.58 0.18] | 31.7 | 67.1 | 113 | |||
| P3 | 113 | [−0.99 0.13 −0.06] | 49.4 | [−0.93 0.25 −0.28] | 25.8 | 66.8 | 127 | 104 | [0.99 0.13 −0.07] | 48.3 | [0.89 0.46 0.05] | 37.5 | 61.2 | 119 | |||
| P4 | 106 | [−0.95 0.30 0.06] | 47.6 | [−0.82 0.56 0.13] | 30.8 | 62.7 | 97.6 | 107 | [0.97 0.22 −0.08] | 47.9 | [0.86 0.51 −0.08] | 31.8 | 62.8 | 105 | |||
| P5 | 121 | [−1.00 0.09 −0.02] | 52.1 | [−0.95 0.22 −0.21] | 23.4 | 71.3 | 125 | 111 | [0.98 0.16 0.12] | 49.6 | [0.89 0.14 0.42] | 31.6 | 65.1 | 105 | |||
| P6 | 106 | [−0.93 0.35 −0.12] | 48.9 | [−0.74 0.65 −0.16] | 36.7 | 62.2 | 131 | 108 | [0.93 0.34 −0.13] | 49.4 | [0.75 0.61 −0.24] | 35.1 | 63.5 | 105 | |||
| P7 | 113 | [−0.97 0.22 0.11] | 47.7 | [−0.94 0.34 −0.02] | 17.2 | 66.7 | 114 | 114 | [0.99 0.14 0.10] | 48.8 | [0.98 0.19 −0.10] | 20.5 | 67.4 | 103 | |||
| P8 | 108 | [−0.94 0.28 −0.21] | 52.4 | [−0.72 0.58 −0.38] | 42.8 | 63.9 | 115 | 105 | [0.94 0.32 −0.10] | 51.0 | [0.73 0.66 −0.20] | 43.3 | 61.9 | 115 | |||
| P9 | 106 | [−0.97 0.21 −0.12] | 47.9 | [−0.85 0.39 −0.36] | 33.0 | 62.4 | 103 | 100 | [0.96 0.23 −0.15] | 44.5 | [0.84 0.46 −0.28] | 29.8 | 59.0 | 117 | |||
| P10 | 105 | [−0.93 0.36 0.11] | 47.9 | [−0.75 0.65 0.13] | 35.1 | 61.6 | 118 | 112 | [0.88 0.47 0.03] | 53.0 | [0.65 0.76 0.10] | 39.3 | 66.2 | 121 | |||
| P11 | 114 | [−0.97 0.19 0.13] | 52.1 | [−0.84 0.46 0.29] | 34.7 | 67.1 | 113 | 115 | [0.98 0.12 0.15] | 49.7 | [0.90 0.23 0.36] | 24.7 | 67.5 | 116 | |||
| P12 | 119 | [−0.93 0.31 0.21] | 56.4 | [−0.73 0.45 0.52] | 40.7 | 69.9 | 107 | 121 | [0.98 0.19 −0.09] | 53.3 | [0.89 0.31 −0.32] | 27.8 | 71.4 | 107 | |||
| P13 | 117 | [−0.95 0.31 −0.07] | 52.5 | [−0.81 0.56 −0.17] | 31.3 | 69.1 | 109 | 111 | [0.96 0.25 −0.13] | 47.7 | [0.89 0.32 −0.34] | 22.7 | 65.3 | 114 | |||
| P14 | 122 | [−0.91 0.41 0.05] | 54.9 | [−0.73 0.68 0.09] | 32.3 | 71.7 | 109 | 118 | [0.92 0.34 −0.17] | 50.9 | [0.84 0.37 −0.39] | 23.8 | 69.4 | 113 | |||
| P15 | 102 | [−0.98 0.18 −0.08] | 44.6 | [−0.90 0.34 −0.27] | 25.5 | 60.4 | 98.0 | 93.3 | [1.00 0.04 −0.08] | 39.4 | [0.96 0.17 −0.20] | 17.5 | 55.0 | 99.1 | |||
| P16 | 106 | [−0.92 0.40 −0.06] | 48.3 | [−0.73 0.68 −0.06] | 34.8 | 62.2 | 132 | 109 | [0.91 0.40 −0.10] | 47.9 | [0.77 0.61 −0.19] | 27.3 | 64.3 | 117 | |||
| P17 | 102 | [−0.94 0.24 −0.25] | 47.3 | [−0.76 0.49 −0.42] | 36.5 | 60.3 | 110 | 99.3 | [0.95 0.26 −0.19] | 45.9 | [0.77 0.53 −0.35] | 36.4 | 58.5 | 100 | |||
| P18 | 102 | [−0.96 0.26 −0.06] | 46.8 | [−0.82 0.57 −0.11] | 34.8 | 60.3 | 114 | 102 | [0.97 0.24 −0.10] | 47.4 | [0.81 0.55 −0.19] | 37.6 | 60.0 | 116 | |||
| P19 | 118 | [−0.97 0.17 0.15] | 51.7 | [−0.92 0.39 0.01] | 26.5 | 69.6 | 109 | 123 | [0.97 0.19 0.16] | 53.5 | [0.88 0.42 0.22] | 24.9 | 72.7 | 118 | |||
| P20 | 110 | [−0.94 0.28 −0.21] | 51.2 | [−0.77 0.61 −0.17] | 37.9 | 64.5 | 105 | 112 | [0.94 0.28 −0.19] | 52.7 | [0.77 0.61 −0.18] | 38.9 | 66.1 | 121 | |||
| P21 | 95.1 | [−0.95 0.24 −0.18] | 45.3 | [−0.79 0.60 −0.16] | 40.6 | 56.1 | 97.3 | 101 | [0.95 0.30 0.01] | 47.5 | [0.78 0.63 0.03] | 38.2 | 59.8 | 105 | |||
| P22 | 107 | [−0.96 0.24 −0.15] | 44.9 | [−0.91 0.28 −0.30] | 16.3 | 63.0 | 113 | 110 | [0.90 0.42 −0.09] | 51.1 | [0.69 0.71 −0.12] | 37.2 | 64.8 | 115 | |||
| P23 | 108 | [−0.98 0.16 −0.11] | 46.2 | [−0.93 0.19 −0.32] | 21.6 | 63.6 | 115 | 111 | [0.98 0.20 0.00] | 50.0 | [0.87 0.48 −0.10] | 32.1 | 65.4 | 117 | |||
| P24 | 100 | [−0.96 0.29 −0.02] | 45.3 | [−0.81 0.58 −0.04] | 32.5 | 59.1 | 112 | 100 | [0.95 0.32 −0.02] | 45.3 | [0.80 0.59 0.04] | 32.3 | 59.2 | 121 | |||
| P25 | 99.0 | [−0.91 0.41 0.04] | 45.9 | [−0.71 0.70 0.09] | 36.7 | 58.4 | 96.5 | 98.6 | [0.96 0.27 −0.01] | 41.6 | [0.95 0.24 −0.18] | 16.9 | 58.1 | 110 | |||
| P26 | 103 | [−0.98 0.11 −0.15] | 43.2 | [−0.94 0.20 −0.27] | 15.1 | 60.8 | 128 | 102 | [0.97 0.23 0.02] | 44.2 | [0.89 0.43 0.13] | 24.3 | 60.2 | 131 | |||
| P27 | 105 | [−0.95 0.32 0.04] | 45.7 | [−0.88 0.43 −0.19] | 26.3 | 61.6 | 106 | 105 | [0.94 0.33 0.00] | 48.6 | [0.77 0.64 −0.04] | 36.5 | 61.9 | 113 | |||
| P28 | 98.9 | [−0.96 0.21 −0.17] | 42.1 | [−0.90 0.40 −0.19] | 20.0 | 58.3 | 115 | 100 | [0.97 0.15 −0.17] | 44.5 | [0.88 0.43 −0.20] | 29.9 | 58.9 | 124 | |||
| C1 | 125 | [−0.97 0.21 0.08] | 57.4 | [−0.84 0.51 0.21] | 35.8 | 73.5 | 114 | 115 | [0.97 0.19 0.12] | 51.4 | [0.86 0.44 0.25] | 31.3 | 67.6 | 114 | |||
| C2 | 122 | [−0.98 0.21 0.02] | 51.3 | [−0.93 0.37 0.04] | 15.8 | 72.0 | 114 | 120 | [0.98 0.17 −0.11] | 51.6 | [0.92 0.25 −0.31] | 22.0 | 71.0 | 109 | |||
| Min | 95.1 | 42.1 | 15.1 | 56.1 | 94.1 | 93.3 | 39.4 | 16.9 | 55.0 | 99.1 | |||||||
| Max | 125 | 57.4 | 42.8 | 73.5 | 132 | 123 | 53.5 | 45.5 | 72.7 | 131 | |||||||
| Range | 29.6 | 15.3 | 27.6 | 17.4 | 37.6 | 30.0 | 14.2 | 28.6 | 17.7 | 31.9 | |||||||
| Avg | 109 | [−0.96 0.26 −0.04] | 48.8 | [−0.86 0.50 −0.10] | 29.9 | 64.3 | 112 | 108 | [0.97 0.25 −0.04] | 48.7 | [0.87 0.49 −0.08] | 30.9 | 63.8 | 113 | |||
| Std | 8.05 | [0.13 0.59 0.79] | 3.78 | [0.29 0.54 0.79] | 8.07 | 4.75 | 10.0 | 7.45 | [0.20 0.66 0.73] | 3.49 | [0.28 0.59 0.76] | 7.41 | 4.39 | 7.58 | |||
Table A.4.
Optimal configuration of MDS as defined by its radius (r) and its location relative to the cochlea (p), using the brute-force method. Vectors are expressed in the RAS convention, where +x is directed to the person’s right side, +y is directed anteriorly, and +z is directed superiorly. Units are in {mm} except for the unitless direction vector from the cochlea toward the MDS center.
| ID | Left |
Right |
|||||
|---|---|---|---|---|---|---|---|
| ||p|| |
|
r | ||p|| |
|
r | ||
| P1 | 100 | [−0.96 0.28 −0.08] | 58.8 | 100 | [0.95 0.28 −0.13] | 59.1 | |
| P2 | 112 | [−0.95 0.32 0.00] | 65.8 | 114 | [0.94 0.30 0.14] | 67.1 | |
| P3 | 112 | [−0.99 0.12 −0.04] | 66.1 | 103 | [0.99 0.12 −0.09] | 60.8 | |
| P4 | 105 | [−0.96 0.28 0.04] | 62.1 | 106 | [0.98 0.20 −0.09] | 62.7 | |
| P5 | 120 | [−0.99 0.11 0.04] | 70.9 | 109 | [0.99 0.13 0.09] | 64.3 | |
| P6 | 103 | [−0.94 0.29 −0.17] | 60.9 | 105 | [0.96 0.23 −0.17] | 61.6 | |
| P7 | 113 | [−0.98 0.17 0.14] | 66.4 | 112 | [0.97 0.14 0.18] | 66.1 | |
| P8 | 105 | [−0.93 0.16 −0.33] | 62.1 | 104 | [0.93 0.17 −0.34] | 61.5 | |
| P9 | 105 | [−0.98 0.18 −0.12] | 62.0 | 100 | [0.96 0.22 −0.17] | 59.0 | |
| P10 | 104 | [−0.94 0.34 0.08] | 61.4 | 100 | [0.95 0.29 0.06] | 58.8 | |
| P11 | 113 | [−0.98 0.15 0.11] | 66.8 | 113 | [0.99 0.07 0.08] | 66.7 | |
| P12 | 111 | [−0.96 0.26 0.07] | 65.6 | 114 | [0.96 0.26 0.07] | 67.1 | |
| P13 | 117 | [−0.96 0.27 −0.11] | 68.8 | 109 | [0.96 0.26 −0.09] | 64.5 | |
| P14 | 117 | [−0.94 0.31 −0.13] | 69.0 | 117 | [0.93 0.34 −0.13] | 68.9 | |
| P15 | 102 | [−0.98 0.05 −0.18] | 60.4 | 93.1 | [1.00 0.08 −0.02] | 54.9 | |
| P16 | 104 | [−0.93 0.37 −0.06] | 61.1 | 110 | [0.92 0.38 −0.10] | 64.6 | |
| P17 | 101 | [−0.95 0.21 −0.22] | 59.4 | 97.4 | [0.96 0.21 −0.21] | 57.4 | |
| P18 | 101 | [−0.96 0.23 −0.13] | 59.7 | 101 | [0.97 0.19 −0.16] | 59.5 | |
| P19 | 118 | [−0.99 0.14 0.08] | 69.8 | 123 | [0.98 0.18 0.13] | 72.2 | |
| P20 | 109 | [−0.94 0.26 −0.20] | 64.0 | 110 | [0.96 0.24 −0.15] | 64.8 | |
| P21 | 94.9 | [−0.96 0.22 −0.19] | 55.9 | 97.2 | [0.95 0.21 −0.23] | 57.3 | |
| P22 | 105 | [−0.95 0.32 0.01] | 62.1 | 102 | [0.94 0.31 −0.12] | 60.2 | |
| P23 | 103 | [−0.99 0.14 −0.01] | 61.0 | 108 | [0.99 0.14 −0.03] | 63.9 | |
| P24 | 100 | [−0.96 0.28 −0.02] | 59.1 | 101 | [0.95 0.31 −0.04] | 59.3 | |
| P25 | 94.4 | [−0.94 0.35 −0.03] | 55.7 | 97.5 | [0.95 0.31 0.02] | 57.5 | |
| P26 | 102 | [−0.98 0.18 −0.07] | 60.4 | 101 | [0.98 0.21 0.01] | 59.6 | |
| P27 | 104 | [−0.95 0.30 0.06] | 61.0 | 101 | [0.96 0.28 0.08] | 59.4 | |
| P28 | 97.9 | [−0.97 0.16 −0.16] | 57.7 | 99.2 | [0.98 0.13 −0.16] | 58.5 | |
| C1 | 123 | [−0.98 0.20 0.03] | 72.7 | 114 | [0.99 0.15 0.07] | 67.5 | |
| C2 | 122 | [−0.98 0.18 −0.02] | 71.9 | 119 | [0.99 0.10 −0.11] | 70.2 | |
| Min | 94.4 | 55.7 | 93.1 | 54.9 | |||
| Max | 123 | 72.7 | 123 | 72.2 | |||
| Rng | 28.9 | 17.1 | 29.4 | 17.4 | |||
| Avg | 107 | [−0.97 0.23 −0.05] | 63.3 | 106 | [0.98 0.21 −0.05] | 62.5 | |
| Std | 7.89 | [ 0.15 0.58 0.80] | 4.65 | 7.40 | [0.13 0.52 0.84] | 4.36 | |
Table A.5.
Placement, relative to the cochlea, of an MDS oversized to 75 mm radius. Vectors are expressed in the RAS convention. The values represent the centroid of all the valid points anterior to the cochlea, where the oversized MDS can be placed without collision and satisfy the magnetic field requirement. Units are in mm except for the unitless direction vector .
| ID | Left |
Right |
|||
|---|---|---|---|---|---|
| ||v|| |
|
||v|| |
|
||
| P1 | 122 | [−0.95 0.32 −0.03] | 122 | [0.96 0.29 −0.04] | |
| P2 | 124 | [−0.94 0.33 −0.01] | 124 | [0.95 0.29 0.08] | |
| P3 | 125 | [−0.99 0.16 −0.03] | 123 | [0.98 0.17 −0.08] | |
| P4 | 123 | [−0.96 0.29 0.01] | 123 | [0.97 0.24 −0.06] | |
| P5 | 126 | [−0.99 0.12 0.04] | 124 | [0.98 0.20 0.05] | |
| P6 | 122 | [−0.94 0.31 −0.11] | 122 | [0.95 0.30 −0.08] | |
| P7 | 124 | [−0.98 0.20 0.03] | 124 | [0.98 0.20 0.05] | |
| P8 | 122 | [−0.97 0.24 −0.08] | 121 | [0.97 0.23 −0.05] | |
| P9 | 122 | [−0.98 0.21 −0.03] | 121 | [0.97 0.24 −0.05] | |
| P10 | 122 | [−0.92 0.39 0.01] | 121 | [0.95 0.32 0.02] | |
| P11 | 125 | [−0.98 0.15 0.09] | 125 | [0.99 0.13 0.11] | |
| P12 | 124 | [−0.96 0.26 0.04] | 125 | [0.97 0.24 0.03] | |
| P13 | 125 | [−0.96 0.27 −0.09] | 123 | [0.95 0.31 −0.09] | |
| P14 | 125 | [−0.94 0.34 −0.08] | 125 | [0.93 0.36 −0.10] | |
| P15 | 122 | [−0.97 0.21 −0.08] | 120 | [0.97 0.22 −0.07] | |
| P16 | 123 | [−0.92 0.39 −0.03] | 124 | [0.91 0.40 −0.10] | |
| P17 | 122 | [−0.96 0.26 −0.10] | 121 | [0.96 0.28 −0.08] | |
| P18 | 121 | [−0.97 0.23 −0.06] | 121 | [0.98 0.20 −0.07] | |
| P19 | 125 | [−0.98 0.16 0.11] | 126 | [0.98 0.17 0.11] | |
| P20 | 124 | [−0.95 0.28 −0.13] | 124 | [0.96 0.24 −0.13] | |
| P21 | 121 | [−0.97 0.25 −0.02] | 121 | [0.96 0.28 −0.01] | |
| P22 | 122 | [−0.95 0.30 −0.05] | 122 | [0.95 0.32 −0.05] | |
| P23 | 123 | [−0.97 0.23 −0.05] | 124 | [0.98 0.20 −0.04] | |
| P24 | 121 | [−0.95 0.31 −0.03] | 121 | [0.94 0.33 −0.04] | |
| P25 | 120 | [−0.93 0.35 −0.04] | 121 | [0.95 0.31 −0.02] | |
| P26 | 122 | [−0.98 0.20 −0.05] | 121 | [0.97 0.23 −0.02] | |
| P27 | 122 | [−0.96 0.27 −0.01] | 121 | [0.96 0.27 0.00] | |
| P28 | 120 | [−0.97 0.24 −0.07] | 121 | [0.98 0.20 −0.10] | |
| C1 | 127 | [−0.98 0.17 0.04] | 125 | [0.98 0.15 0.11] | |
| C2 | 126 | [−0.98 0.19 0.01] | 125 | [0.98 0.18 −0.05] | |
| Min | 120 | 120 | |||
| Max | 127 | 126 | |||
| Rng | 6.44 | 6.04 | |||
| Avg | 123 | [−0.96 0.26 −0.03] | 123 | [0.97 0.25 −0.03] | |
| Std | 1.74 | [0.21 0.74 0.64] | 1.68 | [0.21 0.64 0.74] | |
References
- 1.Zeng FG, Rebscher S, Harrison W, Sun X, Feng H. Cochlear implants: System design, integration, and evaluation. IEEE Rev Biomed Eng. 2008;1:115–142. doi: 10.1109/RBME.2008.2008250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wardrop P, Whinney D, Rebscher SJ, Roland JT, Jr, Luxford W, Leake PA. A temporal bone study of insertion trauma and intracochlear position of cochlear implant electrodes. I: comparison of Nucleus banded and Nucleus Contour electrodes. Hear Res. 2005;203(1–2):54–67. doi: 10.1016/j.heares.2004.11.006. [DOI] [PubMed] [Google Scholar]
- 3.Carlson ML, Driscoll CL, Gifford RH, McMenomey SO. Cochlear implantation: Current and future device options. Otolaryngologic Clinics of North America. 2012;45(1):221–248. doi: 10.1016/j.otc.2011.09.002. [DOI] [PubMed] [Google Scholar]
- 4.Wanna GB, Noble JH, Gifford RH, Dietrich MS, Sweeney AD, Zhang D, Dawant BM, Rivas A, Labadie RF. Impact of intrascalar electrode location, electrode type, and angular insertion depth on residual hearing in cochlear implant patients: Preliminary results. Otol Neurotol. 2015;36(8):1343–1348. doi: 10.1097/MAO.0000000000000829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wanna GB, Noble JH, Carlson ML, Gifford RH, Dietrich MS, Haynes DS, Dawant BM, Labadie RF. Impact of electrode design and surgical approach on scalar location and cochlear implant outcomes. Laryngoscope. 2014;124(S6):S1–S7. doi: 10.1002/lary.24728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Clark JR, Leon L, Warren FM, Abbott JJ. Magnetic guidance of cochlear implants: Proof-of-concept and initial feasibility study. J Med Devices. 2012;6(3):035002. [Google Scholar]
- 7.Leon L, Cavilla MS, Doran MB, Warren FM, Abbott JJ. Scala-tympani phantom with cochleostomy and round-window openings for cochlear-implant insertion experiments. J Med Devices. 2014;8(4):041010. [Google Scholar]
- 8.Leon L, Warren FM, Abbott JJ. An in-vitro insertion-force study of magnetically guided lateral-wall cochlear-implant electrode arrays. Otol Neurotol. 2018;39(2):e63–e73. doi: 10.1097/MAO.0000000000001647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mahoney AW, Abbott JJ. Generating rotating magnetic fields with a single permanent magnet for propulsion of untethered magnetic devices in a lumen. IEEE Trans Robot. 2014;30(2):411–420. [Google Scholar]
- 10.Furlani EP. Permanent Magnet and Electromechanical Devices. Academic Press; 2001. [Google Scholar]
- 11.Wright SE, Mahoney AW, Popek KM, Abbott JJ. The spherical-actuator-magnet manipulator: A permanent-magnet robotic end-effector. IEEE Trans Robot. 2017;33(5):1013–1024. [Google Scholar]
- 12.Petruska AJ, Abbott JJ. Omnimagnet: An omnidirectional electromagnet for controlled dipole-field generation. IEEE Trans Magn. 2014;50(7):8400810. [Google Scholar]
- 13.Spitzer V, Ackerman MJ, Scherzinger AL, Whitlock D. The visible human male: A technical report. J Am Med Inform Assoc. 1996;3(2):118. doi: 10.1136/jamia.1996.96236280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Techniques for visualizing scalar volume data Mathworks (Natick, MA).
- 15.Xu J, Xu SA, Cohen LT, Clark GM. Cochlear view: Postoperative radiography for cochlear implantation. Am J Otol. 2000;21(1):49–56. [PubMed] [Google Scholar]
- 16.Noble JH, Labadie RF, Majdani O, Dawant BM. Automatic segmentation of intracochlear anatomy in conventional CT. IEEE Trans Biomed Eng. 2011;58(9):2625–32. doi: 10.1109/TBME.2011.2160262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Roland PS, Gstöttner W, Adunka O. Method for hearing preservation in cochlear implant surgery. Oper Tech Otolaryngol Head Neck Surg. 2005;16(2):93–100. [Google Scholar]
- 18.Schuster D, Kratchman LB, Labadie RF. Characterization of intracochlear rupture forces in fresh human cadaveric cochleae. Otol Neurotol. 2015;36(4):657–661. doi: 10.1097/MAO.0000000000000573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.K & J Magnetics Inc. 2017 http://www.kjmagnetics.com/specs.asp.
- 20.Bell B, Gerber N, Williamson T, Gavaghan K, Wimmer W, Caversaccio M, Weber S. In vitro accuracy evaluation of image-guided robot system for direct cochlear access. Otol Neurotol. 2013;34(7):1284–1290. doi: 10.1097/MAO.0b013e31829561b6. [DOI] [PubMed] [Google Scholar]
- 21.Warren FM, Balachandran R, Fitzpatrick JM, Labadie RF. Percutaneous cochlear access using bone-mounted, customized drill guides: Demonstration of concept in vitro. Otol Neurotol. 2007;28(3):325–329. doi: 10.1097/01.mao.0000253287.86737.2e. [DOI] [PubMed] [Google Scholar]
- 22.Bruns TL, Webster RJ., III An image guidance system for positioning robotic cochlear implant insertion tools. SPIE Medical Imaging. 2017 [Google Scholar]
- 23.Romans LE. Computed Tomography for Technologists: A Comprehensive Text. Wolters Kluwer Health - Lippincott Williams & Wilkins; 2010. [Google Scholar]