Addressable electron spin resonance using donors and donor molecules in silicon

Built-in hyperfine couplings of donor qubits engineered by precision placement promote addressable electron spin resonance.

Abstract

Phosphorus donor impurities in silicon are a promising candidate for solid-state quantum computing due to their exceptionally long coherence times and high fidelities. However, individual addressability of exchange coupled donors with separations ~15 nm is challenging. We show that by using atomic precision lithography, we can place a single P donor next to a 2P molecule 16 ± 1 nm apart and use their distinctive hyperfine coupling strengths to address qubits at vastly different resonance frequencies. In particular, the single donor yields two hyperfine peaks separated by 97 ± 2.5 MHz, in contrast to the donor molecule that exhibits three peaks separated by 262 ± 10 MHz. Atomistic tight-binding simulations confirm the large hyperfine interaction strength in the 2P molecule with an interdonor separation of ~0.7 nm, consistent with lithographic scanning tunneling microscopy images of the 2P site during device fabrication. We discuss the viability of using donor molecules for built-in addressability of electron spin qubits in silicon.

INTRODUCTION

Phosphorus donor atoms in silicon are very attractive as the basis of a solid-state quantum computer, because they combine the long-lived quantum memory of a nuclear spin with the rapid control and strong interactions possible with an electron spin (1). With weak coupling to their environment, phosphorus donors in isotopically purified ²⁸Si have demonstrated minute-long nuclear (2) and millisecond-long electron (3) spin coherence times. In addition, high-fidelity single-qubit quantum gate operations using resonant magnetic fields (4) and high-fidelity state readout (5, 6) have recently been demonstrated for single P donor qubits.

Because of the strong Coulomb potential well, donors provide a means of producing uniform electron spin qubits with reproducible tightly confined wave functions and thus a nondegenerate, low-lying valley and orbital ground state. To achieve an accurate entangling two-qubit quantum gate, via the exchange (7, 8) or dipole (9) interaction, donors must be placed with high precision and on the order of tens of nanometers apart. We achieve this fine positional control through scanning tunneling microscope (STM) hydrogen-resist lithography (10), which has an effective resolution less than the silicon lattice constant. Therefore, one of the challenges is to individually address nominally identical qubits when they are very close together. In gate-defined silicon quantum dot single-spin qubits, typically placed ~100 nm apart, the necessary addressability in electron spin resonance (ESR) has been achieved via a slanting Zeeman field generated by a surface micromagnet (11) or via a Stark shift in the ESR peaks (12). Similar tunability of qubit resonance frequencies has been observed for a single-donor qubit (13). However, in moving to multiqubit systems, with ~15-nm interdonor separations, a higher B- or E-field gradient will be needed to avoid overlapping qubit resonance frequencies (14).

Here, we demonstrate the successful implementation of an alternate strategy for addressing donor-bound electron spin qubits. We use the differentiated hyperfine coupling of an electron confined by the potential well formed by a single P donor and by a pair of donors in a donor molecule (14, 15). We show ESR measurements of the hyperfine spectrum of both a single donor (1P) and a donor molecule (2P) within a single double quantum dot device.

The spin states of each individual quantum dot may be described by the generalized Hamiltonian containing an electron Zeeman term and nuclear Zeeman terms as well as hyperfine interaction terms for each donor nucleus, i.

$$\mathit{H}={\mathit{g}}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{B}}{\mathit{B}}_0{\mathit{S}}_{\mathrm{z}}+{\displaystyle \sum _{\mathit{i}}}{\mathit{g}}_{\mathrm{n}}{\mathrm{\mu }}_{\mathrm{N}}{\mathit{B}}_0{\mathit{I}}_{\mathit{i}\mathrm{z}}+{\displaystyle \sum _{\mathit{i}}}\overrightarrow{\mathit{S}}·({\mathit{A}}_{\mathit{i}}\mathbf{I}+{\mathbf{D}}_{\mathit{i}})·{\overrightarrow{\mathit{I}}}_{\mathit{i}}$$

Here, g_e(g_n) is the electron (nuclear) g factor, μ_B(μ_N) is the Bohr (nuclear) magneton, and S (I) is the electronic (nuclear) spin angular momentum. The static magnetic field B₀ is oriented parallel to the patterned surface and aligned with the 110 crystal axis, and the hyperfine coupling tensor for each nuclei i is decomposed into a scalar Fermi contact interaction part A_i and an anisotropic dipolar component D_i, which is often treated as negligible.

RESULTS

Alignment of ESR antenna

The device presented is a planar donor-defined nanostructure, in which two-dimensional regions of a silicon crystal are heavily phosphorus-doped beyond the metal-insulator transition by STM hydrogen resist lithography, to produce gates, reservoirs, and also localized charge islands (10). Figure 1 (A and B) shows the lithographic mask at the two quantum dot sites, relative to the 2 × 1 dimer reconstruction on the silicon surface during fabrication. To incorporate a single P atom, we require three adjacent exposed dimers. This permits the phosphine gas (PH₃) molecule to fully dissociate at the surface (16). From the images (both showing five consecutive exposed dimers), we expect at least one P atom in each quantum dot, with a possibility for two at the left site due to the presence of multiple additional exposed dimers nearby. The actual number of donors incorporated at each site was subsequently verified by measuring each quantum dot’s charging energy. Here, we determined the single-electron addition energies to be E_2P ~ 65 meV and E_1P ~ 43 meV, consistent with NEMO-3D tight-binding simulations reflecting 2P and 1P for the left and right quantum dot, respectively (17). These assignments are further confirmed by the following ESR results. The two sites are separated by 16 ± 1 nm and are both tunnel-coupled (at a distance of 19 nm) to a larger charge-sensing single-electron transistor (SET), as shown in Fig. 1C, for energy-selective spin readout (18). The SET additionally functions as an electron reservoir for the two donor sites. Figure 1D shows the full layout including electrostatic gates, where red regions represent metallic conductive structures of delta-doped epitaxial silicon, with a carrier density of n = 2.5 × 10¹⁴ cm⁻² (19). The conducting phosphorus structures are buried below a 55-nm-thick encapsulation layer and contacted by etching vias and depositing aluminum surface contacts.

Fig. 1. Alignment of a surface ESR antenna to the buried atomic precision double quantum dot.

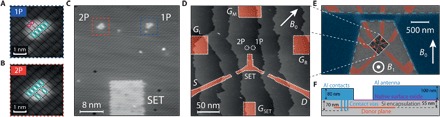
(A) Atomic resolution STM image of the single donor (1P) quantum dot and (B) donor molecule (2P) quantum dot. A rectangular black grid, with reactive exposed dimers highlighted in green and single unreactive exposed Si atoms marked in pink, indicates the 2 × 1 surface reconstruction of dimers. (C) High-resolution STM image of the two quantum dots and the readout SET and (D) larger-scale image showing the full device structure. False-colored red areas are phosphorus-doped to form the sensor SET, source and drain leads, and electrostatic gates. (E) False-color composite scanning electron microscopy and STM image showing the buried donor structures (red) relative to the aluminum surface antenna (blue), which generates an oscillating B₁ field out of the plane, as indicated. The direction of the B₀ field produced by a superconducting magnet is also shown. (F) Vertical cross-section, showing the thickness (not to scale) and relative position of the silicon, phosphorus, oxide, and aluminum layers. The Al contacts are not seen in (A) to (E), as they are positioned >1 μm away from the antenna.

Following initial characterization of the device including independent spin readout and spin correlation measurements (20), a broadband microwave antenna was postfabricated on the chip. This is a remarkable feature of donor-based all-epitaxial devices. Because the dopant layer is protected by the crystalline silicon environment, which is conductive (ρ ~ 10 ohm·cm) at room temperature due to background doping, electrostatic discharge is unlikely. Hence, these devices can be measured at cryogenic temperatures (where background dopants freeze out) multiple times and be reprocessed to add additional surface gates, waveguides, or antennas, before being measured again.

The antenna geometry is impedance matched (21) to minimize radiative and reflective loss of microwave power while maximizing the oscillating magnetic field, B₁. The postfabrication process requires additional electron beam lithography, achieved with positional uncertainty of <200 nm relative to the buried atomic scale device, by reference to pre-etched alignment markers (22). Physical vapor deposition of 100 nm of aluminum onto the naturally oxidized silicon surface produces an antenna capable of withstanding up to 2 V DC bias relative to the buried phosphorus layer with minimal current leakage (R > 100 gigohms). The inner region of the completed antenna is seen in Fig. 1E (colored blue), positioned with the donors inside the loop of the antenna where the simulated ratio of oscillating magnetic field, B₁, to in-plane oscillating electric fields is maximized (see section S1). A vertical cross-section of the device structure is shown in Fig. 1F.

Addressable resonance spectra

We operate in the high magnetic field regime (B > 1.2 T) such that g_eμ_BB₀ > A > g_nμ_NB₀, where the eigenstates are, to first order, separable into electron and nuclear subspaces, and we perform our measurements at ~50 mK in a dilution refrigerator. The spin resonance experiment proceeds by applying voltages proportionally to the left and right gates to detune the donor potential relative to a fixed SET Fermi energy (see section S2). Because the electron spin relaxation time is much longer than the characteristic tunneling time between SET and donor, we initialize the state by ionizing the donor and deterministically loading an electron in the spin down state |↓〉. The donor-bound electron is in Coulomb blockade while a microwave pulse is applied. This is followed by a single-shot readout sequence in which spin-dependent tunneling (14, 18) converts the projected electron spin state to a charge state, observable via the SET current signal.

The sequence used for the 2P molecule is equivalent, but instead of conditionally ionizing the molecule by removing the single electron, it uses a spin-dependent transition into the two-electron spin-singlet state (23) for readout. This technique has the additional benefit of faster tunneling rates, which permits faster operation relative to the single donor (1P). Our microwave ESR pulses are applied with a nominal power at the signal generator of +5 dBm (we estimate ~60 dB attenuation at the device) for 150 μs and modulated with a linear frequency chirp of ±20 MHz. This adiabatic passage pulse (24) inverts the electron spin eigenstates irrespective of the exact pulse duration or precise instantaneous resonance frequency, enhancing our spin resonance signal (25). The spin resonance spectrum of the single donor (1P) is shown in Fig. 2A for B₀ = 1.35 T. These data show the fraction of |↑〉 outcomes, p_↑, over 640 single-shot measurements at each frequency, f. (Additional spin resonance data are provided in section S3.) We observe two peaks, corresponding to the resonance conditions for driving transitions between electron |↓〉 and |↑〉 states when the single nuclear spin state is either |⇓〉 (left peak) or |⇑〉 (right peak). The transition frequencies here are ${\mathit{f}}_{\Downarrow }={\mathit{g}}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{B}}{\mathit{B}}_0-\frac{{\mathit{A}}_{1\mathrm{P}}}{2}$ and ${\mathit{f}}_{\Uparrow }={\mathit{g}}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{B}}{\mathit{B}}_0-\frac{{\mathit{A}}_{1\mathrm{P}}}{2}$, separated by the single-donor hyperfine coupling strength A_1P. The solid curve in Fig. 2A is a fit to the sum of two Gaussian peaks sharing a common full width at half maximum Δf_FWHM = 27.8 ± 2 MHz and with amplitudes p_⇓ = 0.18 and p_⇑ = 0.46.

Fig. 2. ESR spectra for a single P donor and a 2P molecule.

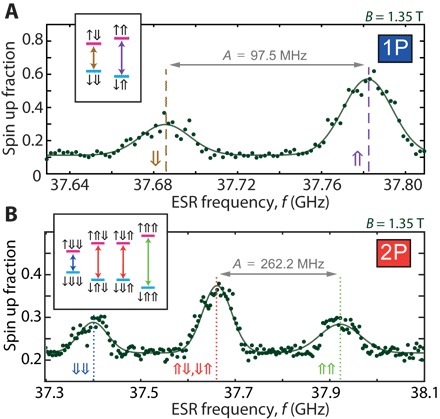
(A) Measured ESR spectrum for the 1P bound electron and (B) 2P donor molecule at B₀ = 1.35 T using a ±20 MHz adiabatic passage frequency chirp. Insets indicate the nuclear (double arrow) and electron (single arrow) spin eigenstates and the ESR transitions between them, each corresponding to an observed resonance peak. The measured hyperfine energies A_1P and A_2P are indicated for each donor quantum dot.

The hyperfine coupling strength A_1P = f_⇑ − f_⇓ = 96.5 ± 2.5 MHz for the single P atom is comparable to other values reported in the literature ranging from 96.9 to 116.6 MHz for P donors ion implanted in a nanoelectronic device (4, 13). In these papers, the difference between the hyperfine coupling strength reported for single donors in a nanoelectronic device and that reported for bulk ensembles of P donors, ~117.5 MHz (26), was attributed to a Stark shift due to the electric field within the device. Such an electric field perturbs the electron wave function, reducing the electron density over the nucleus and giving rise to a quadratic Stark effect in P donors (27, 28). In our device, we have an electric field at the 1P site of E ~ 4.5 MV/m (see section S4) such that A_1P is reduced by a factor of 2.5 × 10⁻³ (MV/m)⁻², or ~6 MHz due to this effect. While of the same order of magnitude as the observed 21-MHz reduction, other influences may also come into play. One such effect is the uniformity or alignment of electric and magnetic fields in the device (29, 30). We note that in Fig. 2A, the |⇑〉 peak has more than twice the amplitude of the |⇓〉 resonance, indicating that there is some polarization of the nuclear spin, with the |⇑〉 state more likely to be occupied than |⇓〉. This polarization reflects nuclear spin dynamics likely arising from an inelastic electron-nuclear flip-flop process, pumped by spin resonant excitation at the f_⇓ frequency (31, 32). Here, an electron spin “flips” from |↑〉 to |↓〉, and the nuclear spin simultaneously “flops” from |⇓〉 to |⇑〉. The total spin is thus conserved, and energy conservation is satisfied by the emission of a phonon. Because the energy difference between the states is larger than the thermal energy g_eμ_BB₀ > k_BT, the reverse transition involving absorption of a phonon is suppressed. Any alternate cross-process involving the |↓⇓〉 and |↑⇑〉 states would require a change in total spin of ±1 and so is forbidden by spin conservation. We infer from fluctuations in our recorded spin-up signal over time (see sections S5 and S6 for further analysis on the nuclear dynamics) that the time scale for the flip-flop process may be as short as 50 s, orders of magnitude faster than expected for P donors at our magnetic field and temperature (31, 32). We may attribute this increased rate to an enhancement in the electron-phonon interaction due to the nontrivial valley structure of the electric field–perturbed wave function inside our nanostructure (33). Partial repopulation of the state can be explained by an “ionization shock” (6), where misalignment of the nuclear spin eigenstates in the neutral and ionized donor charge states provides a small nonzero probability of flipping the nuclear spin on each electron ionization event. In Fig. 2B, we show the resonance spectrum measured for the electron bound to the 2P molecule. These data are based on 2000 single shots (compared to 640 for the 1P single donor due to the faster tunnel rate between the SET and 2P molecule), with a microwave pulse power of +8 dBm and the same chirp parameters as above. Here, we observe three resonant frequencies. The solid curve is a fit to three Gaussian peaks of width Δf_FWHM = 72 ± 5 MHz and amplitudes: p_⇓⇓ = 0.072, p_{⇓⇑/⇓⇑} = 0.158, and p_⇑⇑ = 0.067. The three peaks reflect the transition frequencies, shown in the inset to Fig. 2B, separated by A_a and A_b, the contact hyperfine interaction coefficients representing the electron wave function density at the location of the two donor sites (labeled a and b) of the 2P molecule. At zero electric field, the 2P electron wave function is symmetric and the hyperfine interaction at the two donor sites is expected to be equal A_a = A_b, producing two degenerate transition frequencies f_⇓⇑ = f_⇑⇓. However, at the operating point of the 2P molecule in our device, we calculate an electric field of around 4.3 MV/m (see sections S4 and S8), which serves to break this degeneracy A_a ≠ A_b. Because we resolve only one central peak in the resonance spectrum, the hyperfine asymmetry |A_a − A_b| must be less than the width of the observed peak ~72 MHz. The average peak separation, representing the donor molecule hyperfine interaction energy A_2P = (A_a + A_b)/2 = 264 ± 10 MHz, is more than twice the single donor value, consistent with the anticipated range for a pair of donors with small (<1 nm) spatial separation (15). We can calculate the Stark shift expected for the 2P molecule for the same electric fields (see section S8). The value ranges from <10 kHz (with the electric field perpendicular to the molecular axis of the 2P molecule) to 6 MHz (with the electric field parallel to the molecular axis of the 2P molecule). We note that the asymmetry in the peak amplitudes seen in the 1P case is absent in the 2P molecule’s ESR spectrum. In Fig. 2B, we see an equal probability for each of the four nuclear spin state resonances. The nuclear |⇓⇑〉 and |⇑⇓〉 states are approximately degenerate and indistinguishable, producing a peak with approximately twice the amplitude of the |⇓⇓〉 and |⇑⇑〉 resonances.

To understand the nuclear spin dynamics in the 2P molecule, we consider the full tensor form of the hyperfine interaction Σ_i=a,b A_iI + D_i, which, for each of the donors, consists of the Fermi contact hyperfine scalar A, proportional to the electron wave function density at the position of a donor atom and the traceless dipole-dipole interaction tensor D (see section S6). Because donor atoms have a strong Coulomb confinement, the electron wave function is highly concentrated over the donor nuclei, and A dominates by several orders of magnitude over D for a single donor, even with significant perturbation by an electric field (27, 34). The dipolar tensor is expected to be more anisotropic in the case of the molecular 2P wave function (35), because it is inherently nonspherical. We find that there is no correlation in the nuclear spin state between successive electron readout events, confirming a significant enhancement of the ionization shock mechanism relative to that observed for the single donor. In short, the nuclear spin state in the 2P molecule is randomized faster than it is polarized by any inelastic relaxation.

Next, we turn to consider the disparity in resonance linewidths in the 1P and 2P cases, important as this reflects the coherence properties of the bound electron spin. The 1P resonance peaks have a linewidth of 27.8 ± 2 MHz as a result of being artificially broadened by the 20-MHz linear frequency chirp we apply to our microwave pulse to adiabatically invert the spin state. The spin dephasing time for a single P donor in natural silicon was recently measured as 55 ns (36) corresponding to a natural linewidth (FWHM) around 10 MHz. This is limited by random fluctuations in the local magnetic field due to the presence of ²⁹Si nuclear spins. We use the adiabatic pulse strategy (24, 25) to combat the fluctuations and selected the chirp span to cover the expected natural linewidth. The 2P resonances are markedly wider at 72 ± 5 MHz, which we attribute to a stronger interaction between the bound electron and local nuclear spins within the 2P wave function envelope, as compared to the single donor. While this suggests a dephasing time of <10 ns for the current 2P bound electron, using isotopically purified silicon substrate has the potential to suppress nuclear spin–limited decoherence. Recent results have shown that moving to isotopically pure ²⁸Si has increased the coherence time of electron spins on single P donors from 100 μs to 0.5 s (4). It will be interesting to see if these enhanced dephasing times are possible for 2P electron qubits.

Hyperfine metrology of donor position

Given the atomic scale of our device, it is possible to model the full-electron wave functions, accounting for the silicon lattice and band structure, donor potentials, and the potential profile across the nanostructure. Hence, we compare our measured 2P hyperfine coupling strength, A_2P, with atomistic tight-binding simulations. From the size of the lithographic patches (Fig. 1, A and B), we restrict ourselves to consider pairs of lattice sites within a distance of 1 nm. Figure 3 shows the calculated hyperfine energy within a 2P molecule hosting a single electron, where we vary the location and thus the separation between the two P atoms. The data points in Fig. 3 indicate the A_2P values for various configurations, where both donors lie in the [001] crystallographic plane, for four different interatomic distances r < 1 nm (additional out-of-plane donor configurations are discussed for comparison in section S7). The general trend is a reduction in the hyperfine interaction with increasing donor separation, as expected. However, the interplay between the tetrahedral symmetry of the silicon crystal lattice around the donor atom and the cubic symmetry of the six conduction band minima in the silicon bulk gives rise to a highly structured 2P wave function with deviations from a smooth exponential decay curve that is dependent on the orientation of the donor pair with respect to the crystal lattice (15, 37). The dominant uncertainty in the calculated hyperfine coupling A_2P is due to the potential Stark shift that could be observed in such a system for the electric field strength and orientation used in the device (see section S8). The magnitude of the uncertainty (<5%) is reflected by the size of the markers themselves.

Fig. 3. Atomistic tight-binding modeling of the 2P hyperfine energy.

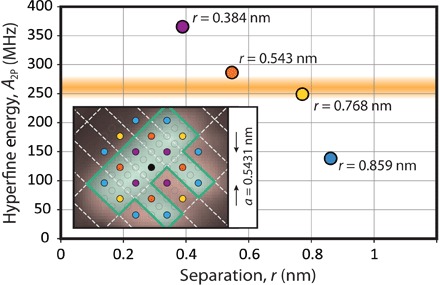
Simulated hyperfine interaction energy A_2P for atomic configurations of a 2P donor molecule with donor separation less than 1 nm in the fabrication plane. The dominant uncertainty is due to incomplete knowledge of the Stark shift, reflected in the size of the markers (<5%). An orange band marks the experimentally observed value of A_2P in our device. The inset shows a schematic of the [001] crystal plane in which the device is fabricated, overlaid on the STM image taken during fabrication (from Fig. 1B). Atoms in this plane are shown colored according to their distance from the central black reference site. The marked green zone denotes a potential layout of fully exposed dimers, consistent with the STM image, where it is possible for a PH or PH₂ fragment to attach to the surface. Small gray circles represent the location of atoms within the crystal lying in layers above and below the fabrication plane, and white lines indicate the grid of surface dimers.

Over the past decade, research on the Si:P system has established that during an anneal at 340°C, a phosphorus atom incorporates into the surface layer of silicon, forming a P-Si heterodimer with a strong phosphorus-silicon bond (16). Consequently, when encapsulated with silicon in a low temperature (250°C) epitaxial growth process (38), calculations indicate that the P-Si bond is resilient to segregation or diffusion (39). Experimental evidence confirms that the donor atom remains localized (40, 41) in the crystal at the lithographically defined site to an uncertainty on the order of one lattice constant. The orange band represents the hyperfine energy measured experimentally for our 2P molecule, A_2P = 262 ± 20 MHz. The geometrical layout of the in-plane configurations of donors are displayed in the inset, color-coded to the hyperfine energy plot. Because of lattice symmetry, there are several equivalent sites for the second P atom, at any given distance from the central reference site (colored black), which represents the location of the first P atom of the molecule. Considering our experimental value of A_2P, only the eight geometries colored orange and yellow are likely representations of the relative configuration of donors in our device. These are consistent with the size of the lithographic patch that was fabricated, as can be seen with reference to the surface dimer reconstruction marked by dashed lines.

An interesting feature observed in our resonance measurements is a relative offset in the central frequencies, evident when the 1P and 2P spectra are displayed on a single axis as in Fig. 4A. To gain an understanding of this offset, we examine the magnetic field dependence of the resonant frequencies. Figure 4 (B and C) plots the relative offset in resonance frequencies for the 1P electron (2P electron) as a function of magnetic field. The values plotted are obtained from fits to the recorded spectra at each magnetic field setting, with a linear Zeeman term subtracted $\mathit{f}\prime =\mathit{f}-{\mathit{g}}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{B}}{\mathit{B}}_0$ for clarity. The electron g factor used in each figure is obtained by a linear fit to each data set, producing values of g_e = 1.988 ± 0.02 (1P) and g_e = 1.986 ± 0.02 (2P). These are both consistent with the bulk g factor of 1.9985 for donor-bound electrons (26, 42), with a 1% uncertainty limited by the current-to-field calibration of our superconducting magnet. The offset between the central frequencies of the 1P and 2P spectra δf′ ~ 45 MHz remains constant across the field range. In magnetic field terms, this corresponds to ~1.6 mT, consistent with the 0.2% difference in g factor we observe between the 1P and 2P cases. We attribute this variation to a Stark shift of the g factor (43, 44), because the electric field is different in both magnitude and direction for our two quantum dots (see section S4). The difference in peak splitting measured for our 1P and 2P sites A_2P − A_1P ~ 165 MHz, as shown in Fig. 4A, is considerably larger than any variability expected from a Stark shift of the hyperfine coupling or g factor, for either the single P atom or 2P molecule.

Fig. 4. Magnetic field dependence and Stark shift of the electron g factor.

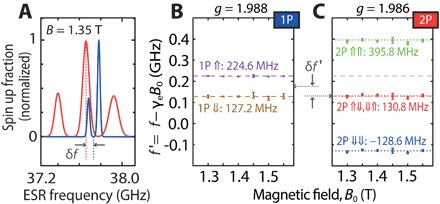
(A) Normalized spin resonance spectra for the 1P (blue) and 2P (red) measured at 1.35 T plotted together to highlight the relative frequencies. (B and C) Frequency offsets $\mathit{f}\prime =\mathit{f}-{\mathit{g}}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{B}}{\mathit{B}}_0$ as a function of magnetic field B₀ for the 2 (3) resonances of the 1P donor (2P molecule) relative to the linear slope of the Zeeman term gμ_BB₀/h. With a shared y axis, an offset due to a Stark shift of the g factor is evident between the two spectra.

DISCUSSION

The range of hyperfine values available for closely separated 2P molecules means that our addressing scheme can be extended to multiple qubits. For instance, using the four different 2P hyperfine interaction strengths shown in Fig. 3, along with a single donor, may produce five individually addressable qubits with unique resonance frequencies, and with an offset between them greater than the inhomogeneous broadening due to nearby nuclear spins, or electric field shifts. An area requiring further investigation, however, is to determine the impact of multiple host ³¹P nuclear spins on coherence times and the overall electron spin dynamics.

We note that hosting single electrons in donor molecules carries a number of additional benefits beyond the intrinsic frequency detuning, including extended T₁ relaxation times (45) and deeper confinement of the two-electron charge state. The latter is particularly relevant for implementing singlet-triplet–based qubits using donor-bound electrons and to realize SWAP-type two-qubit gates (46, 47). The use of larger donor molecules, patterned by STM hydrogen lithography, provides additional scope for wave function engineering and permits strong confinement of multielectron states, as required to achieve Pauli spin blockade for high-fidelity state readout (48). These results represent an important step toward achieving full control over multiple donor spin qubits in silicon. The addressability demonstrated, with frequency detunings an order of magnitude larger than the inhomogeneous linewidth in natural silicon, will facilitate selective control over individual qubits with low cross-talk. Combined with isotopically purified ²⁸Si and nuclear magnetic resonance control over the nuclear spin states (49), donor molecules provide individual addressability for electron spin qubits, and are attractive for quantum simulation and multiqubit architectures.

MATERIALS AND METHODS

The STM hydrogen lithography was performed in ultrahigh vacuum with an Omicron Variable Temperature instrument. A chemically cleaned Si(001) wafer was annealed at 1100°C and passivated in a beam of atomic hydrogen. The hydrogen mask was removed in the required areas by scanning with a tip voltage of around 3 to 6 V and current set point of 1 to 10 nA. Following lithography, the wafer was dosed with phosphine gas and then heated to incorporate the P donors (16) before a 55-nm encapsulation layer of epitaxial silicon was grown at a rate of 0.15 nm/min. The donor layer was electrically contacted by depositing aluminum onto contact vias formed by reactive ion etching. The contact structures, as well as the microwave antenna, were all defined by electron beam lithography using a poly(methyl methacrylate) mask.

Measurements were performed in a ³He/⁴He dilution refrigerator with a base temperature of 50 mK. A superconducting solenoid magnet provided the external magnetic field. DC voltage signals applied to the gates were generated with Yokogawa 7651 and Stanford Research Systems SIM928 voltage sources. Voltage pulses were generated with a National Instruments USB6363 DAC/ADC device and added to the DC signals with simple resistive voltage dividers. The combined gate control signals were then filtered with two-stage lumped element RC filters inside the dilution refrigerator with a low-pass cutoff of 150 kHz, and additional high frequency (>GHz) noise was suppressed with distributed “Eccosorb LS” radio frequency absorber material within the filter enclosure. The microwave signals were supplied to the on-chip antenna from a Keysight E8267D vector signal generator (with phase and pulse modulation signals supplied using a Tektronix 5014C arbitrary waveform generator) via a lossy stainless steel coaxial cable (and additional 1-dB attenuator at 4 K). The readout signal was collected from the SET with a low-noise Femto DLPCA200 transimpedance amplifier and then electrically decoupled and filtered with a Stanford Research Systems SIM910 JFET isolation amplifier and SIM965 Bessel filter before being digitized with the National Instruments USB6363 DAC/ADC.

Our tight-binding method uses the NEMO-3D atomistic solver. The model applies an adjustable cutoff potential at the donor site (a central-cell correction), while elsewhere each donor potential is Coulombic (15). This model of the central-cell correction has been successful in reproducing the full single-donor spectrum, the Stark shifts of the hyperfine coupling (28), as well as the system g factor, the orbital energies of the bound electrons, and replicating STM-based imaging of the donor wave function. The Schrodinger and Poisson equations are then self-consistently solved within a 30-nm cubic domain to produce the ground-state wave function from which the hyperfine interaction strength is computed for each donor.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/7/eaaq1459/DC1

Section S1. Microwave antenna alignment and field simulations

Section S2. Initialization and readout pulse sequence

Section S3. Wideband frequency scans

Section S4. Static electric field simulations

Section S5. 1P nuclear spin dynamics

Section S6. 2P nuclear spin dynamics

Section S7. Atomistic tight-binding modeling

Section S8. Tight-binding model of 2P hyperfine Stark shift

Fig. S1. Finite element microwave field simulations.

Fig. S2. Pulse protocol incorporating continuous interleaved monitoring of charge stability.

Fig. S3. ESR across a wide frequency band.

Fig. S4. Electric fields at the 1P and 2P qubit operating points.

Fig. S5. Development of asymmetry in the 1P hyperfine spectrum with increasing magnetic field.

Fig. S6. Populations of the 2P nuclear states remain independent of the magnetic field.

Fig. S7. Intrinsic hyperfine energies for different donor configurations of a 2P molecule.

Fig. S8. Computed Stark shift of the hyperfine coupling.

Table S1. Gate settings and resultant E-field estimates.

Table S2. Atomic separation vectors and calculated hyperfine coefficients.

References (50–53)