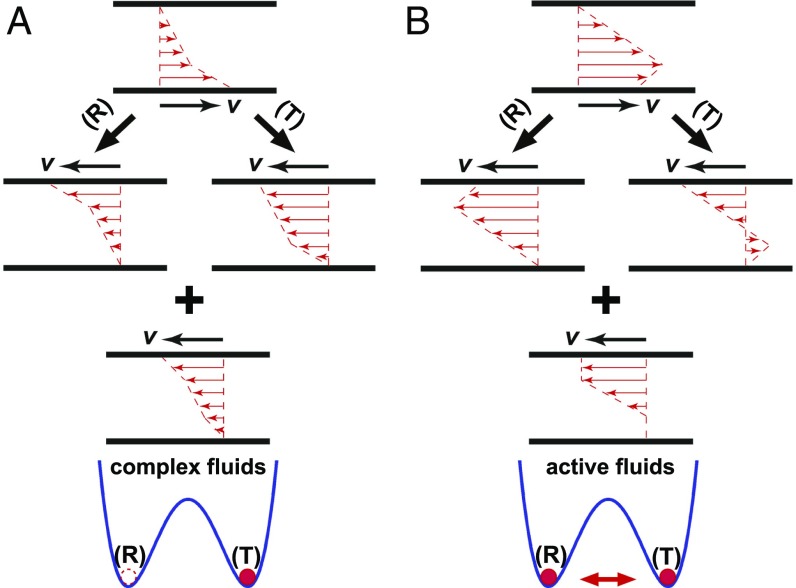
Fig. 7.

Comparison of shear banding in complex and active fluids. (A) Shear banding in conventional complex fluids. The shear-banding flow breaks the symmetry of unsheared samples, which can be seen from the difference in the shape of shear profiles after two physical operations: (i) a rotational operation (R), where the system is rotated counterclockwise by $\pi$, and (ii) a translational operation (T), where the laboratory frame is transformed into a moving frame of a linear velocity $-V$. Although the boundary conditions of the systems after the two operations are the same, the resulting shear profiles are different. Thus, the sheared sample before the operations cannot simultaneously satisfy the translational and rotational symmetry of the unsheared sample. The ensemble average of the two symmetry-broken shear configurations is approximately linear, restoring the original symmetry of the unsheared sample. A sheared complex fluid chooses one of the two symmetry-broken configurations, depending on initial and/or boundary conditions. The symmetry-broken process is illustrated schematically by the location of a red circle in a split-bottom potential, in analogy to the spontaneous symmetry breaking in equilibrium phase transitions. The valleys (R) and (T) indicate the two possible symmetry-broken shear-banding configurations. (B) Shear banding in active fluids. The ensemble-averaged shear profile from the two symmetry-broken shear-banding configurations is symmetric and nonlinear. A sheared active fluid samples both symmetry-broken configurations and preserves the symmetry of the unsheared fluid.