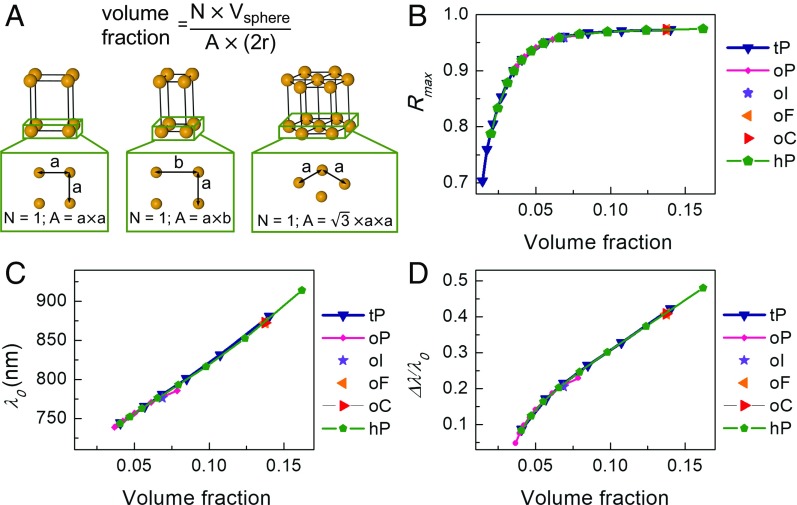
Fig. 3.
The volume fraction of each NP layer dictates the Rmax, λ0, and Δλ/λ0 of the stopband. (A) The volume fraction within each NP layer is defined in the equation, where N is the number of NPs in each unit cell, Vsphere is the volume of the NP, and A × (2r) is the volume of a unit cell: A is the area of the facet in the x–y plane of the unit cell, r is the radius of the NP. Thus, the diameter of the NP defines the thickness of the NP layer. (B) Rmax, (C) λ0, and (D) normalized bandwidth (Δλ/λ0) of tP, oP, and hP lattices as a function of volume fraction within each NP layer. One lattice constant within the NP layer is chosen for body-centered orthorhombic (oI), face-centered orthorhombic (oF), and base-centered orthorhombic (oC), and the stopband features show good agreement with the oP lattices as predicted. The layer periodicity of all data points is 240 nm.