From genome-wide associations to candidate causal variants by statistical fine-mapping

Abstract

Advancing from statistical associations of complex traits with genetic markers to understanding the functional genetic variants that influence traits is often a complex process. Fine-mapping can select and prioritize genetic variants for further study, yet the multitude of analytical strategies and study designs makes it challenging to choose an optimal approach. We review the strengths and weakness of different fine-mapping approaches, emphasizing the main factors that affect performance. Topics include interpreting results from genome-wide association studies (GWAS), the role of linkage disequilibrium, statistical fine-mapping approaches, trans-ethnic studies, genomic annotation and data integration, and other analysis and design issues.

Graphical Abstract

Fine-mapping is the process by which a trait-associated region from a genome-wide association study (GWAS) is analysed to identify the particular genetic variants that are likely to causally influence the examined trait. This Review discusses the diverse statistical approaches to fine mapping, their foundations, strengths and limitations, including integration of trans-ethnic human population data and functional annotations.

Introduction

Common complex human traits¹ — including quantitative traits and diseases — often result from multiple environmental and genetic causes. Genome-wide association studies [G] (GWAS)¹ have been widely used to identify the genomic regions on chromosomes that harbour genetic determinants of complex traits [G]^2–8. To date, 47,681 statistical associations of single-nucleotide polymorphisms (SNPs) with complex traits are summarized in the US National Human Genome Research Institute (NHGRI)–European Bioinformatics Institute (EBI) GWAS Catalog⁹, representing 2,185 traits with association p-values less than 10⁻⁵. This success can be attributed to cost-efficient genotyping microarrays containing a large number of SNPs. However, the SNPs on microarrays typically do not cause¹⁰ the trait. Rather, the SNPs on microarrays, called tag-SNPs [G], are chosen because they are highly correlated (i.e., large amount of linkage disequilibrium [G] (LD)) with neighbouring SNPs, thereby serving as surrogates for large genomic regions that contain unmeasured SNPs^11,12. The association between a tag-SNP and a trait can be indirect, resulting from tag-SNP associated with a causal SNP, which in turn is associated with a trait. Because patterns of LD among SNPs can be complex, it can be challenging to determine the underlying causal variants [G]. This is when fine-mapping [G] can help¹³. The principles discussed here are also relevant for common genetic variants measured by whole-genome sequencing studies.

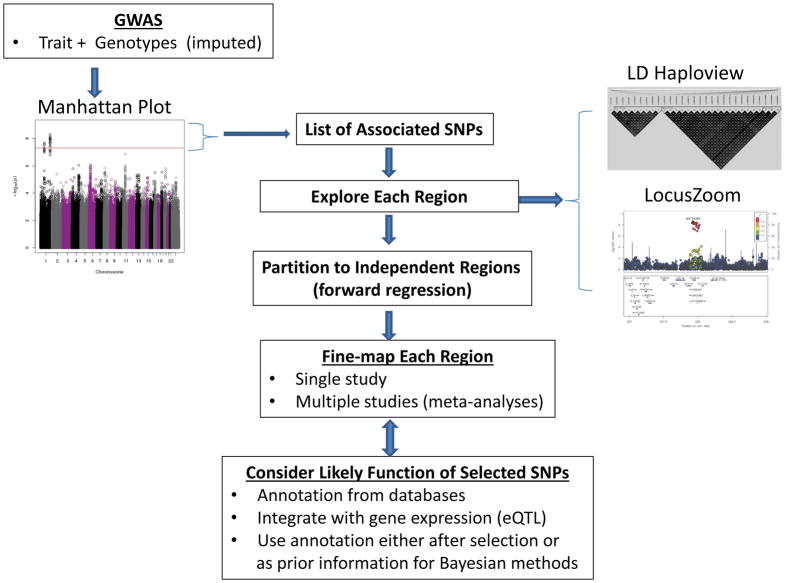
Fine-mapping seeks to determine the genetic variant (or variants) responsible for complex traits, given evidence of an association of a genomic region with a trait, and assuming at least one causal variant exists. After an initial GWAS identifies at least one SNP strongly associated with a trait (e.g., p-value <5×10⁻⁸), fine-mapping typically proceeds by the general steps outlined in Figure 1. These steps will be discussed in detail, but the general strategy is to use the GWAS list of SNPs associated with a trait to identify regions of interest. Each region is then visually explored for its LD structure and for genes known to be mapped to the region. Because it is simpler to fine-map one causal variant at a time, each region is partitioned into sub-regions that have approximately independent effects on the trait. Next, a fine-mapping strategy is chosen. The strategies we will discuss are illustrated in Figure 2. The selected SNPs are further evaluated for their likely function based on publicly available genomic annotation in order to prioritize costly and time-consuming laboratory-based functional studies.

Figure 1. Flow of typical process from intial GWAS to annotation of SNPs selected from fine-mapping analyses.

Based on GWAS p-values summarized in a Manhattan plot¹¹², a list of SNPs that achieve genome-wide statistical significance (i.e., p-value <5×10⁻⁸) is used to determine regions of interest for fine-mapping. Each region is typlically explored according to the structure of linkage disequilibrium among single-nucleotide polymorphisms (SNPs) using Halpoview plots. Statistical assocaitions are viewed with LocusZoom plots that illustrate the patterns of association of each SNP with the lead SNP, as well as annotation of genes in the region. The regions can then be partitioned into independent sub-regions to ease computational burden, based on statistical models that evalute the simultaneous effects of multiple SNPs on a trait. Statistical fine-mapping is conducted in each region, using one of the methods illusrated in Figure 2. The SNPs selected from fine-mapping are then annotated with genomic features to prioritize follow-up functional studies. Figure is adapted from REF¹¹².

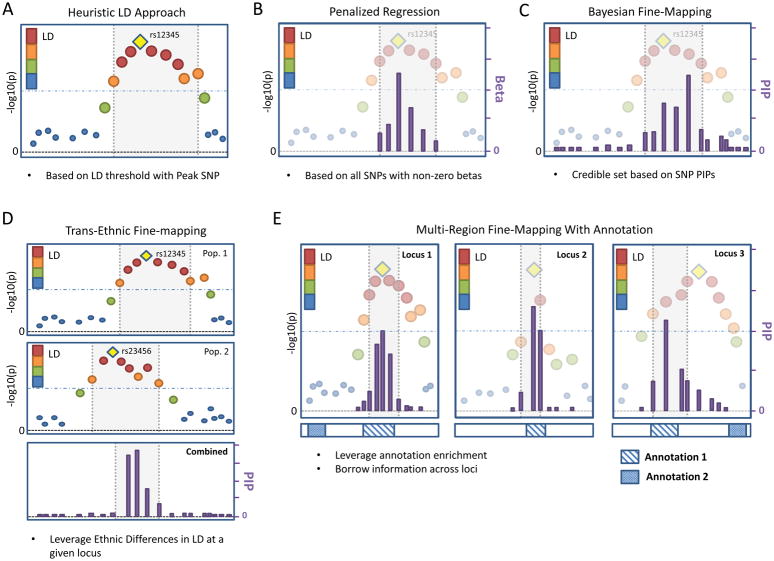
Figure 2. Hypothetical examples of fine-mapping strategies.

All subfigures are based on LocusZoom-style illustrations of marginal single-nucleotide polymorphism (SNP) associations. The −log₁₀(p-values) are presented on the left y-axis and variant positions are on the x-axis. The gold diamond for each locus represents the peak SNP. The results for other SNPs are coloured by descending degree of linkage disequilibrium (LD) with the peak SNP (ordered red, orange, green, and blue dots). The purple bars represent additional variant-level statistics produced by fine-mapping (i.e., Beta values for penalized regression; posterior inclusion probabilities (PIPs) for Bayesian methods ), and the corresponding scale is on the right y-axis. The light grey boxes represent the regions selected by fine-mapping. A | The heuristic approach is based on LD patterns with the peak SNP (rs12345). All SNPs that meet the orange LD category threshold have been selected. B | The penalized regression approach selects all SNPs whose effects (Beta, right axis) are not shrunk to zero. C | Bayesian fine-mapping produces SNP-level PIPs (right axis), which can be summed to form credible sets based on a specified coverage probability threshold (e.g., 95%). This example illustrates that the peak SNP does not correspond to the SNP with the highest PIP, which can occur because of the correlation structure among all SNPs in the region. D | Bayesian trans-ethnic fine-mapping. Results for the same locus are illustrated for two diverse study populations (Pop. 1 (panel Da) and Pop. 2 (panel Db)) with different local LD structures. The peak SNPs for the two analyses differ (rs12345 versus rs23456), and combining the results through meta-analysis yields a narrowed fine-mapping credible region (panel Dc). E | Joint analysis of multiple loci by integrating annotation in Bayesian fine-mapping can improve fine-mapping by borrowing annotation information across loci. Presented are three example independent loci (panels Ea–c) along with two corresponding regional annotations, indicated by bands below each locus plot. For loci 1 and 2, the peak SNPs overlap with Annotation 1, indicating enrichment. This enrichment results in the SNP with the highest PIP in locus 3 to be different from the peak SNP in locus 3.

The main focus of this Review is on the statistical methods used to fine-map each region of interest. The overarching goal is to determine which variants are most likely to be functional, and to quantify the strength of evidence. This information can then be used for follow-up studies, such as large-scale replication studies of specific candidates, or laboratory functional studies. Although the initial GWAS can provide statistical evidence that a region is likely to harbour a causal variant, additional statistical methods are needed in order to discriminate likely functional variants from variants that are merely correlated with the functional variants. A variety of methods have been used, ranging from simple heuristic methods, to the use of penalized regression [G] for high-dimensional data, to more refined Bayesian methods tailored for fine-mapping (illustrated in Figure 2). Some of the methods can be applied to a single study, or to multiple studies combined by meta-analysis techniques. When combining multiple studies, special techniques have been developed to simplify sharing of data, based on summary statistics [G] ¹⁴. When the ethnic background of subjects differs across studies, trans-ethnic [G] fine-mapping can sometimes improve the resolution of fine-mapping. Each of these topics will be discussed, emphasizing their strengths, weaknesses, and challenges. We also present the main factors that influence power and resolution of fine-mapping, which in turn offer guidance for study designs. We review the use of genomic annotation for fine-mapping, as well as the integration of gene expression data with GWAS data. Finally, we discuss future challenges as our understanding of the genetic basis of complex traits evolves.

Interpreting lead SNPs from GWAS

The decision to fine-map a region typically follows the discovery of genome-wide significant results from a GWAS. It is common to summarize GWAS results with a Manhattan plot of all p-values that measure the marginal association of one SNP at a time with a trait, followed with LocusZoom plots for regions of interest¹⁵ (Figure 1). This allows one to focus on the SNPs with the smallest (that is, most significant) p-values in distinct regions, sometimes called the lead or index SNPs. GWAS results are most reliable when SNP associations achieve the accepted genome-wide statistical significance threshold of p-value<5×10⁻⁸ (REFS ^16,17), a threshold that corrects for multiple testing, although some investigators use a weaker threshold of p-value<10⁻⁶ to highlight regions that are ‘suggestive’ of harbouring causal variants.

A limitation of the lead SNP is that there is a reasonable chance that it is not the causal variant. This can occur because GWAS microarrays are based on tag-SNPs, with the tag-SNP merely correlated with the unmeasured causal SNP. Furthermore, even if the causal SNP is measured or imputed, there is a reasonable chance that the statistical association of the causal SNP with the trait is not the most significant association among all the associated SNPs when statistical power [G] is not large. For example, based on simulations with 1,000 cases and 1,000 controls, there was a 79% chance that the lead SNP was found to be causal when the odds-ratio (OR) for disease risk was 1.5 and the risk allele frequency was 50%, but only a 2.4% chance when the OR was 1.1 and the risk allele frequency was 5%¹⁸. Zaykin et al.¹⁹ considered multiple causal variants and the impact of LD and drew similar conclusions that true associations are not likely to result in the smallest p-values, in part due to the small effect sizes of variants on complex traits. These findings emphasize the importance of caution when considering the lead SNP as likely causal, and the importance of fine-mapping in order to identify the causal variant(s).

LD for population fine-mapping

Fine-mapping in population-based studies leverages measures of non-random associations between pairs of loci. When loci are near each other and the frequency of recombination between them is low, the alleles from the different loci that occur on the same chromosome (called a haplotype [G] ) tend to be inherited as a unit. Alleles on a haplotype occurring together more than by chance is referred to as gametic association, or more commonly as linkage disequilibrium (LD). Various measures of LD have been proposed²⁰, but they all depend on the difference between the observed joint frequency of alleles occurring on the same haplotype versus that expected by random chance. The most frequently used measure of LD is a standardized difference, which can be easily estimated by the Pearson correlation between the counts of the minor alleles (i.e., less common alleles) for two SNPs. This correlation coefficient is directly related to statistical power, and it is a reasonable measure for fine-mapping, although for case–control studies of rare diseases, measures such as attributable risk can perform better²¹.

Using LD to fine-map a complex trait is based on the premise that ancestral meiotic recombinations diminish LD, implying that the SNP with the strongest association with a trait is either the causal variant or close to the causal variant. However, evaluating one SNP at a time can be misleading due to the complex patterns of LD in a genomic region. A classic example is the association of Alzheimer’s disease with multiple SNPs around the APOE locus on chromosome 19. As the distance from APOE increases, the p-values for the association of SNPs with disease do not follow a monotonic pattern, but rather increase and decrease²². This opened a debate of whether there are genes in this region other than APOE that cause Alzheimer’s disease. Yet, the large amount of LD in this region has made it challenging to resolve this issue²³. Factors beyond recombination that influence LD are mutation rates of the genetic markers, natural selection, population migrations and admixture, population bottlenecks, and demographic history (e.g., population size and mating patterns)²⁴. Because LD is influenced by factors other than recombination, it is too limiting to rely solely on patterns of pairwise LD, or even haplotype blocks [G], to provide reliable fine-mapping of complex traits.

Factors influencing fine-mapping

A number of factors influence the performance of fine-mapping, including the number of causal SNPs in a region and their effect sizes on the trait, the local LD structure, sample size, SNP density, and whether the causal variants can be measured. Careful definition of the phenotype to enrich for genetic causes (e.g., disease severity, strength of family history) might increase the genetic effect size. The local LD structure is difficult to control, but trans-ethnic meta-analyses can capitalize on differences in LD structure. Factors that can be controlled in study designs are the sample size and SNP density. Sample size can be increased by pooling different studies or performing meta-analyses, recognizing that disease heterogeneity might increase, thus diluting efforts. Because it is critical to have high SNP density to capture the causal variants, in the following section we focus on strategies to increase density.

Increasing SNP density

The density of SNPs can be increased by DNA sequencing, but the costs for sequencing the large sample sizes required for fine-mapping can be prohibitive. Alternative cost-efficient strategies include genotype imputation [G] and additional genotyping.

Genotype imputation

Imputation of SNPs can fill in sporadic missing genotypes, harmonize data from different GWAS genotyping arrays to perform a pooled or meta-analysis, and increase the density of SNPs for fine-mapping^25,26. Key criteria for imputation success are high correlation of directly assayed SNPs with the un-typed SNPs and appropriate reference panels that provide templates for LD patterns and allele frequencies that are representative of the study sample²⁵. Popular reference panels are the 1000 Genomes Project²⁷ and the Haplotype Reference Consortium²⁸. Although imputed SNPs tend to be robust to the choice of quality control filters²⁹, power to detect associations with a trait decreases as imputation accuracy decreases²⁵.

Additional genotyping

Because imputation accuracy depends on the local LD structure, regions with weak LD might require actual genotyping to accurately evaluate their association with a trait. Situations where additional genotyping helps are: validation of imputed SNPs, possibly improving fine-mapping by reducing genotype measurement error; discovery of low-frequency SNPs that are not in strong LD with a lead SNP; identification of SNPs that are not well-represented in a reference panel; and disentanglement of SNPs that appear to be in perfect LD because of a small reference sample³⁰.

Cost-efficient genotyping is becoming more accessible with the development of custom genotyping arrays that target certain diseases or traits, such as Oncoarray for common cancers³¹; Metabochip for metabolic, cardiovascular, and anthropometric traits³²; and Immunochip for major autoimmune and inflammatory diseases³³. These specialized arrays are primarily designed to evaluate associations of SNPs that are known to be associated with specific diseases or traits. Notable advantages of these arrays are increased density of SNPs in known gene regions and cost efficiency to achieve large sample sizes for fine-mapping. However, there are limitations. First, array content is focused on SNPs or genes that are already known to be associated with specific diseases or traits, which might exclude finding novel genes. These arrays also contain a backbone of genome-wide tag-SNPs that might overcome this limitation, albeit at a lower resolution than high-density arrays that are typically used for initial GWAS discovery. Second, array content can be based on reference data with incomplete coverage. Third, array content is based on SNPs rather than structural variation. Fourth, SNPs may be excluded from arrays due to assay failure. Finally, array designs are primarily based on European ancestry.

Partition to independent regions

When analyzing one SNP at a time, it is common to find multiple SNPs in a region to be marginally associated with a trait. This can occur when multiple non-causal SNPs are correlated with a single causal SNP. The LD among the SNPs will make each SNP appear to be associated with a trait when analyzing one SNP at a time. By contrast, when analyzing all SNPs jointly, only the causal SNP is expected to be associated with the trait when accounting for the LD among the SNPs, simplifying fine-mapping efforts. Alternatively, when there are in fact multiple causal SNPs, and they are correlated with each other and with other non-causal SNPs, fine-mapping can be more challenging because joint analyses are not expected to highlight just one causal SNP.

To simplify fine-mapping, it can be advantageous to first partition the region of interest according to the independent effects of SNPs on the trait, and then separately fine-map each partition. To determine if multiple marginally associated SNPs are driven by one or a few independent statistical associations, conditional forward stepwise regression is often used (e.g., logistic regression for case–control studies, or linear regression for quantitative traits). This entails conditioning on the lead SNP from a GWAS by treating it as an adjusting covariate in a regression model and testing the remaining SNPs in the region of interest. If a secondary SNP is found to be statistically significant after adjusting for the primary SNP, the sequential testing proceeds by treating some SNPs as adjusting covariates while screening the remaining SNPs, until no conditional tests are significant. A challenge is to decide on the threshold for significance. Some investigators use the stringent GWAS threshold p-value<5×10⁻⁸, while others use more liberal thresholds, such as p-value<10⁻⁴ or even p-value<0.05.

There are several limitations of forward stepwise conditional regression. First, as the number of steps increases, the number of statistical tests increases. If there are m SNPs, then after k sequential steps approximately km statistical tests will be performed, increasing the chance of a false positive result. Second, when m is large, perhaps close to the number of subjects in the sample, and when a liberal threshold is used to include SNPs at each step, the forward selection procedure becomes unstable³⁴ and is overly optimistic regarding the trait variation explained by the selected SNPs³⁵. Third, the probability (i.e., statistical power) to detect secondary signals diminishes as the correlation among SNPs increases.

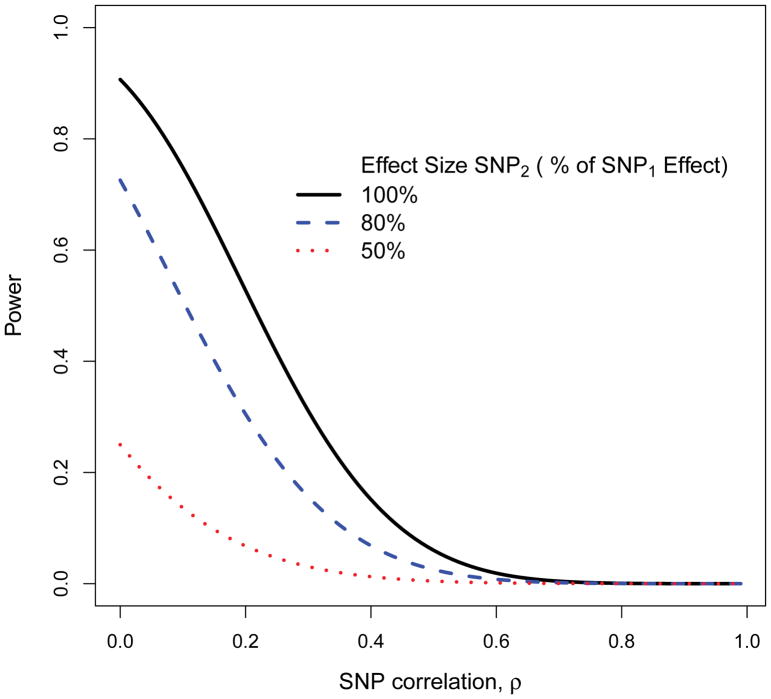
To illustrate diminishing power to detect a secondary SNP by conditional analysis, we derived simple formulas (see Supplementary information S1 (box)) to examine power. We assumed 90% power to detect the primary SNP when it explains 1% of a quantitative trait variation. We set the effect size for the secondary SNP to be a fraction of that for the primary SNP (fraction 50–100%), and we assumed the stringent GWAS threshold p-value<5×10⁻⁸ for testing the effect of the secondary SNP. Figure 3 shows a dramatic loss in power to detect secondary signals as the correlation of SNPs increases, even at levels of SNP correlation ρ=0.2. Power also decreases as the effect size of the secondary SNP decreases. Hence, one should be cautious when using conditional testing to declare only a single SNP to be statistically significant, because low power can cause missed secondary associations.

Figure 3. Power of conditional analysis.

This figure illustrates how conditional analyses have weaker power to detect secondary associated single-nucleotide polymorphisms (SNPs) compared to the power of an initial genome-wide association study (GWAS). Power of conditional analyses diminishes as the correlation of a primary SNP (indicated by SNP₁) and a secondary SNP (indicated by SNP₂) increases, and when the effect size of a secondary SNP is weaker than that for a primary SNP. For this figure, the power for an initial GWAS to detect a primary SNP₁ is 90% for an effect size of R² = 1% of explained trait variation. The effect size of a secondary SNP₂ is varied from 100% to 50% of the effect size of primary SNP₁.

Types of fine-mapping approaches

A number of approaches have been used to perform fine-mapping. We present three main strategies that have been used in the literature: heuristic methods, penalized regression models, and Bayesian methods (illustrated in Figure 2). Heuristic approaches were the first to be used, having grown out of practical experience and educated guesses, but with loosely defined criteria. Penalized regression models were developed in other fields of statistics, with the aim to reduce high-dimensional predictor variables (e.g., SNP data for fine-mapping) to a much smaller set that are strongly associated with a trait. In recent years, Bayesian methods have been specifically tailored for fine-mapping. The main features of these three approaches are discussed, along with their benefits and limitations.

Heuristic fine-mapping approaches

Because the LD structure around the lead SNP from GWAS has a substantial role in fine-mapping, it is popular to first examine the correlation among the SNPs surrounding a lead SNP. One approach is to filter SNPs according to their pairwise correlation (r²) with the lead SNP, retaining as potentially causal only those SNPs with an r² above a threshold. Alternatively, hierarchical clustering of all SNPs in a region based on their pairwise r² has been used to create clusters. However, both of these approaches depend on arbitrary thresholds to filter or form clusters. More rigorous penalized models and Bayesian methods that jointly model the simultaneous effects of multiple SNPs on a trait are more informative.

Another way to view correlation structure is by pairwise LD among SNPs within haplotypes, using software such as Haploview³⁶ (Figure 1). This gives a visual impression of discrete haplotype blocks³⁷. Combining the GWAS lead SNP with SNPs in the same haplotype block is an alternative way to select potential causal SNPs. However, one should be cautious with this approach. Recombination hot-spots [G] strongly influence block features, yet block boundaries can be arbitrary due to the choice of statistical model parameters and computational method, as well as genetic marker density and allele frequencies^38,39. Internal inconsistencies of blocks are troubling, such as when two markers in strong LD flank markers with little LD with one of the flanking markers³⁸. The above heuristic methods to choose SNPs for functional follow-up are too limiting because they do not account for the joint effects of the SNPs on the trait, and they do not give an objective measure of the confidence that a SNP is causal, but rather rely on somewhat arbitrary thresholds and subjective interpretations of correlations among SNPs.

Penalized regression models

An alternative fine-mapping approach is to use a regression model to jointly analyze all the SNPs in a region. Traditional model building is based on forward selection (or alternative stepwise methods), using p-values to determine whether a SNP should be included in a model. However, a large number of SNPs, and high correlation among the SNPs, can make traditional regression models unstable. A more robust approach is provided by penalized regression models. These models simultaneously perform estimation of SNP effect sizes and SNP selection into a model by shrinking small effect estimates toward zero. Popular penalized models are lasso⁴⁰, elastic net⁴¹, minimax concave penalty⁴², and a normal-exponential-gamma shrinkage prior⁴³ implemented in the hyperlasso software. Simulation studies show that penalized models tend to perform better than forward selection. Forward selection can be too conservative when using a very stringent p-value threshold to select SNPs, yet a liberal threshold increases the chance of falsely selecting SNPs⁴⁴. Penalized models use tuning parameters to select SNPs into a model, with tuning parameters chosen to encourage SNPs with small effect sizes to be removed from the model. Tuning parameters are often estimated by cross-validation [G] to choose a model with minimum prediction error. Penalized models tend to result in sparse models, selecting only one or a few SNPs belonging to a group of correlated SNPs. This can result in a good prediction model that includes non-causal SNPs and excludes a causal SNP when they are highly correlated. In Supplementary information S1 (box) we provide R code for readers to further see how high correlation combined with sparse models reduces the chance of selecting the causal variant. By contrast, Bayesian methods have been specifically designed for fine-mapping, offering advantages over heuristic and penalized regression approaches.

Bayesian methods overview

The challenge of both penalized regression and Bayesian variable selection methods is to determine which SNPs have non-zero effect sizes (regression β values) on a trait. Although we refer to SNPs with non-zero effect sizes as causal, it is important to realize that statistical methods alone cannot determine causality. Penalized models choose SNPs based on cross-validation that minimizes the error of predicting a trait. By contrast, Bayesian inference focuses on the probability of a specific hypothesis, or specific model, thus providing probabilistic interpretation of models of interest.

A model for fine-mapping can be represented by an indicator variable for each SNP, with values of 1 for causal and 0 for not, and organizing these indicators for all SNPs of interest in vector c. For m SNPs, there are 2^m possible c vectors (hence 2^m possible models), ranging from all values of c equal to 0 for no SNPs causal, to all values equal to 1 for all SNPs causal. Using Bayes’ formula, the prior probability [G] of a model can be combined with the likelihood of the data D (trait and SNPs) to compute the posterior probability [G] of a specified model M_c, which we denote P(M_c | D). See box 1 for how the posterior probability is calculated. There are several ways to specify the prior probability for a model, such as assuming that variants are independent and equally likely to be causal^45,46, or assuming a fixed number of causal variants out of the total variants^46,47 (see Supplementary information S1 (box) for more details). The posterior probabilities for different models can be used to determine the posterior probability of including each SNP in any of the models (posterior inclusion probability [G] (PIP)), as well as determining the minimum set of SNPs required to capture the likely causal SNPs (credible sets). A variety of Bayesian fine-mapping methods have been developed, and are summarized in Table 1.

Box 1. Bayesian methods.

The goal of Bayesian methods is to compute the probability of a specific model, conditional on the observed data, denoted D, which includes the trait and SNPs. For a model M_c specified by a vector c of indicator variables, each indicator variable having values of 1 if a SNP is causal and 0 if a SNP is non-causal, the posterior probability of model M_c is:

$$P(M_c\mid D)=\frac{P(D\mid M_c)P(M_c)}{{\displaystyle \sum _{M\in \mathcal{M}}}P(D\mid M)P(M)},$$

where the sum in the denominator is over all models from a specified model space ℳ. For example, if the model space were to allow exactly one causal SNP out of k SNPs, there would be k possible c vectors, and k possible models in the space ℳ.

The term P(D|M_c) is the probability of the data under an assumed model. If only a fixed set of β values were considered, P(D|M_c) would be the likelihood of the data, denoted P(D|β). This is the same likelihood used in frequentist analyses. But, Bayesian inference treats the β values as random in order to account for their uncertainty. This is accomplished by assuming a prior distribution for the β values, which we denote P(β|M_c), and averaging over their possible values. This leads to the marginal likelihood, computed by integrating over the distribution of β values;

$$P(D\mid M_c)=\int P(D\mid \beta )P(\beta \mid M_c)\partial \beta .$$

The ingredients of Bayesian methods are the likelihood [P(D|β)] and the assumed prior distribution of the models and their parameters. Details regarding choices of likelihood models and prior probabilities for Bayesian fine-mapping, as well as approximate Bayes factors, are discussed in Supplementary information S1 (box).

Table 1.

Commonly used Bayesian fine-mapping software.

Software	Trait typea	Input covariatesb	Uses summary statistics?	Maximum number of causal variantsc	Input annotation?	Causal search	Main output	Refs
BIMBAM v1.0	qt/binary	No	No	Fixed	No	Exhaustive	Bayes factor	113;114
mvBIMBAM v1.0.0 115,116	mqt	No	Yes	1	No	Exhaustive	Bayes factor
SNPTEST v2.5.4-beta3	qt/binary/mqt/multinomial	No	No	1	No	Exhaustive	Bayes factor	117
piMASS v0.9	qt/binary	No	No	Computed	No	MCMC	Bayes factor and PIP	45
BVS v4.12.197,118,119	binary	Yes	No	Computed	Yes	MCMC	Bayes factor and PIP	96,114,115
FM-QTL	qt	No	No	Computed	Yes	MCMC	Bayes factor and PIP	96
DAP v1.0.0	qt	Yes	Yes	1/Fixed/Computed	Yes	Exhaustive	Bayes factor and PIP	52
Fine-mapping	multinomial	Yes	No	Computed	No	Greedy	PIP	30
Trinculo	multinomial	Yes	No	Computed	No	Greedy	Bayes factor and PIP	30,120
BayesFM	binary	Yes	No	20	No	MCMC	PIP	30
ABF	qt/binaryd	Yes	Yes	1	No	Exhaustive	Bayes factor	121
fgwas v0.3.6	qt/binaryd	No	Yes	1	Yes	Exhaustive	Bayes factor and PIP	95
CAVIAR/eCAVIAR	qt/binaryd	No	Yes	Fixed	No	Exhaustive	ρ probability confidence set and PIP	46,101
PAINTOR v3.0	qt/binaryd/mqt	No	Yes	Fixed/Computed	Yes	Exhaustive/MCMC	Bayes factor and PIP	54,57,71
CAVIARBF v0.2.1	qt/binaryd	No	Yes	Fixed	Yes	Exhaustive	Bayes factor and PIP	47,94
FINEMAP v1.1	qt/binaryd	No	Yes	Fixed	No	Shotgun stochastic search	Bayes factor and PIP	53
JAM in R2BGLiMS v0.1	qt/binaryd	No	Yes	Fixed/Computed	No	Exhaustive/MCMC	Bayes factor and PIP	55

^aTrait types are: binary, single binary trait; mqt, multiple quantitative traits; multinomial, trait with more than two categories; and qt, single quantitative trait.

^bFor software that does not allow covariates to be input, the traits can be adjusted for covariates by first regressing out the covariates (i.e., subtracting trait predicted by covariates from trait values).

^cA fixed number is specified by the user, to reduce computational cost. It is usually small (e.g., ≤3) when the number of candidate variants is large. When computed, the number of causal variants is determined by the software. As indicated, some software allow different options for whether the maximum number of causal variants is fixed by the user or computed by the software.

^dApplication to binary traits is based on linear regression, an approximation assuming small effect sizes and large sample sizes. MCMC, Markov chain Monte Carlo; PIP, posterior inclusion probability.

BIMBAM v1.0: http://www.haplotype.org/bimbam.html

mvBIMBAM v1.0.0: http://stephenslab.uchicago.edu/software.html#mvbimbam

SNPTEST v2.5.4-beta3: https://mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest.html

piMASS v0.9: http://www.haplotype.org/pimass.html

BVS v4.12.1: https://cran.r-project.org/web/packages/BVS

FM-QTL: https://github.com/xqwen/fmeqtl

DAP v1.0.0: https://github.com/xqwen/dap

Fine-mapping: https://github.com/hailianghuang/Fine-mapping

Trinculo: https://sourceforge.net/projects/trinculo/

BayesFM: https://sourceforge.net/projects/bayesfm-mcmc-v1-0/

fgwas v0.3.6: https://github.com/joepickrell/fgwas

CAVIAR/eCAVIAR: http://genetics.cs.ucla.edu/caviar/

PAINTOR v3.0: https://github.com/gkichaev/PAINTOR_V3.0

CAVIARBF v0.2.1: https://bitbucket.org/Wenan/caviarbf

FINEMAP v1.1: http://www.christianbenner.com/

JAM in R2BGLiMS v0.1: https://github.com/pjnewcombe/R2BGLiMS

Bayesian methods: posterior inclusion probability

Bayesian methods for fine-mapping have been specialized in order to focus on the SNPs that have the largest chance of being causal^45,48. The PIP for a SNP is the probability of including a SNP as causal in any of the models. For SNP j, the PIP is computed by the sum of the posteriors over all models that include SNP j as causal,

$${\mathit{PIP}}_j=P(c_j=1\mid D)=\sum _{M,c_j=1}P(M\mid D)$$

After the posterior probabilities for the different models are computed, the PIP is rapid to compute and is an output from many Bayesian fine-mapping software packages (Table 1). Ranking SNPs by their PIP is a convenient way to select putative causal SNPs⁴⁶. For example, the top k SNPs ranked by their PIP maximizes the expected number of causal SNPs across all possible subsets of size k⁴⁷. However, caution is warranted when multiple SNPs in a region are highly correlated and all are approximately equally correlated with the phenotype. In this situation, none of the individual PIPs would be very large. It would be better to estimate the posterior expected number of causal SNPs by summing the estimated PIPs for all SNPs in the region⁴⁵.

Bayesian methods: credible sets

Bayesian methods can be used to determine the α credible set⁴⁹, the minimum set of SNPs that contains all causal SNPs with probability α. When assuming only one causal SNP, α is the sum of PIPs for SNPs in a set. This means that an α credible set is equivalent to ranking SNPs from largest to smallest PIPs⁵⁰, and taking the cumulative sum of PIPs until it is at least α.

Bayesian methods can also allow for multiple causal SNPs in a region. Although computation time increases because of the larger number of models required for multiple causal SNPs, recent developments^46,51–54, notably the JAM software⁵⁵, make it feasible to stochastically search over a wide array of possible models. An excellent demonstration of the benefits of Bayesian fine-mapping is provided by a fine-mapping analysis of 84 prostate cancer GWAS loci using 143,804 subjects⁵⁶. Single signals of causal variants were found in 63 regions, and 12 regions showed evidence of multiple independent causal variants. Furthermore, only 15 (5.4%) of the 280 original GWAS tag-SNPs remained as potential causal variants.

There are numerous advantages to Bayesian methods for fine-mapping. First, unlike p-values, posterior probabilities for SNPs can be directly compared. Second, they tend to select fewer SNPs as potentially causative compared to selecting SNPs based on their correlation with the lead SNP¹⁸. Third, simulation studies have shown Bayesian methods to perform better than both conditional stepwise regression^46,55,57 and penalized regression models⁴⁷. Finally, because Bayesian models are based on the joint effects of SNPs, they control for SNPs with large effects, improving power to detect SNPs with lesser effects. See Figure 2 for visual aspects of Bayesian fine-mapping.

Combining studies and meta-analyses

Combining data from multiple cohorts can increase fine-mapping resolution, and the fine-mapping strategies discussed above can be used when individual-level data are pooled. However, because it can be challenging to obtain individual-level data from multiple cohorts, summary statistics for the associations of a trait with SNPs can be used¹⁴. This strategy is gaining popularity because it simplifies data sharing and computational issues. When summary statistics are appropriately chosen, there is no loss of information compared to using individual-level data⁵⁸. Most summary statistics focus on marginal regression β values and their variances. To obtain the joint effects of multiple SNPs using individual-level data, one must regress trait y on all SNPs simultaneously, y = Xβ^J+e, where β^J is a vector of the joint effects of SNPs, X is a matrix of the coded SNP effects (e.g., counts of minor alleles), and e is random error. By contrast, in summary data when only the marginal β values are available, it is still possible to determine the joint effects of SNPs needed for fine-mapping. When effect sizes are small, there is a simple relationship between the joint and marginal effects⁵⁹, determined by β^J = R⁻¹β^M, where β^M is a vector of the marginal effects and R⁻¹ is the inverse of the matrix of pairwise SNP correlations (assuming the columns of X are standardized to have a mean of 0 and a variance of 1). The key aspect is the SNP correlation matrix, which summarizes the LD among the SNPs. When the original data are used to estimate the SNP correlations, there is no loss of information relative to analyzing individual-level data⁵⁸. In practice, an appropriate reference sample is often used to estimate the SNP correlations, such as the 1000 Genomes Project, allowing marginal summary statistics from single SNP analyses to be combined for a joint analysis⁵⁹. However, if the LD patterns in the reference sample do not represent those in the analyzed samples, the estimated joint effects can be biased, leading to errors in fine-mapping. Furthermore, the size of the reference sample should not be too small, and should increase in size as the GWAS sample size increases⁶⁰.

Trans-ethnic fine-mapping

Comparisons of GWAS findings across ethnically diverse populations have revealed that associations of SNPs with complex traits are often consistent across populations, with similar direction of effects of alleles on traits^61,62. Trans-ethnic meta-analyses that combine GWAS results of the same trait across genetically diverse populations can aid fine-mapping by capitalizing on ethnic differences in LD patterns^63,64 (Figure 2).

A critical issue is the choice of ethnic groups. Analyses based on a mix of different European ancestries, or a mix of European and Asian ancestries, provide little gain for fine-mapping^30,65. Rather, simulations have shown that a substantial reduction in the size of Bayesian fine-mapping credible sets can be attained by including subjects of African ancestry⁶⁵, because they have much narrower LD. Including Hispanic ancestry might also improve fine-mapping over using only European or Asian ancestries⁶⁵. The balance of ethnic groups can also impact fine-mapping performance. Simulations have shown that equal proportions of African and European ancestry is optimal for fine-mapping¹⁸. Although current samples with African ancestry tend to be much smaller than those with European ancestry, including African ancestry can still improve fine-mapping resolution⁶⁵.

Trans-ethnic analyses are often conducted as meta-analyses of summary statistics using random-effects methods, recognizing that a SNP can have different effect sizes across different ethnic groups. This heterogeneity can result from differences in study designs, differences due to interactions with other SNPs, or differences due to environmental or lifestyle factors that influence the effects of genes. METASOFT⁶⁶, which implements a modified form of the traditional random-effects approach, is popular among trans-ethnic studies^67–70. Alternative methods that model the heterogeneity can improve fine-mapping resolution. One approach is based on Bayesian methods, as implemented in the PAINTOR software⁷¹. Other approaches that use GWAS SNP data to explicitly adjust for heterogeneity include MANTRA and MR-MEGA. MANTRA is based on a computationally intensive Bayesian partition method that creates discrete clusters of ethnically similar subjects, assuming that subjects within the same cluster have the same allelic effects for a variant, in contrast to subjects from different clusters having different allelic effects⁷². A good example of trans-ethnic fine-mapping with MANTRA, followed by use of PAINTOR and CAVIAR software to estimate PIPs and credible sets, as well as use of functional annotation, is provided in a large fine-mapping study of high density lipoprotein cholesterol⁷³. In contrast to the discrete clusters created by MANTRA, MR-MEGA considers allelic heterogeneity on a continuum, and uses principal components of genetic similarity among subjects to determine axes of genetic variation, and then uses the principal components to adjust for heterogeneity of allelic effect sizes⁷⁴. Simulations show that MR-MEGA can offer improved fine-mapping over other methods, yet retains computational efficiency⁷⁴.

Factors affecting Bayesian PIPs for fine-mapping

A number of factors influence the resolution and power of fine-mapping. To quantify this influence, we derived a simple formula for the expected Bayes PIP of a single causal SNP when studying a quantitative trait (see Supplementary information S1 (box)). This expected posterior probability depends on the effect size of the causal SNP on a trait (measured by multiple regression R², the percent of trait variation explained by the causal SNP) and the sample size (N). Importantly, these two factors combine into the non-centrality parameter that determines power, λ = NR²/(1−R²). Other factors that influence the expected posterior probability are the number of SNPs in the fine-mapping effort (we assume one causal SNP and m non-causal SNPs) and SNP correlation structure. To simplify the correlation structure, we assume that all SNPs are equally correlated with correlation ρ, as might occur when examining a small genomic region, or filtering on SNPs to achieve a correlation threshold. Finally, the assumed prior probabilities that SNPs are causal also influence the posterior probability. Based on these assumptions, the expected posterior probability for a causal SNP can be expressed as

$${\mathit{post}}_c=\frac{{pr}_c}{{pr}_c+{\displaystyle \sum _{\begin{array}{l}i=1\\ i\ne c\end{array}}^m}{pr}_{i}exp\{-(1-\rho )N{R}^2/(1-R^2)\}},$$ (1)

Where pr_i is the prior probability that the i^th SNP is causal, and subscript c is for the causal SNP.

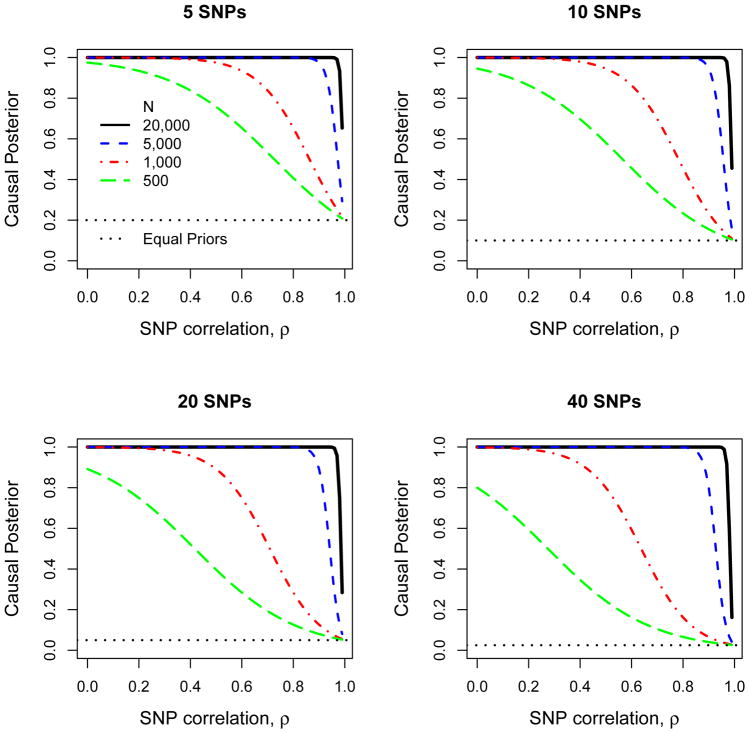
Assuming R² = 1%, a relatively small effect size, we illustrate in Figure 4 that large sample size and small SNP correlations provide the ideal setting to achieve a high posterior probability for a causal SNP. Increasing the number of non-causal SNPs tends to decrease the posterior probability, by spreading out the posterior probability among multiple non-causal SNPs, particularly when the non-centrality parameter λ is not large. Figure 4 also emphasizes that it is difficult to achieve a large posterior probability for a causal SNP when SNPs are highly correlated. Hence, it might be premature to pre-filter SNPs to have a large correlation with a lead SNP before performing fine-mapping efforts, because the SNPs without large correlations could still be viable candidates. Furthermore, when power is weak or SNP correlation is large, well-informed prior probabilities are most critical because in these situations they have a larger effect on the posterior probabilities. Of course, mis-specified prior probabilities can result in a non-causal SNP having a large posterior probability, misleading fine-mapping efforts.

Figure 4. Posterior probability for a single causal SNP when 5–40 SNPs are in a region of interest.

The prior probability that a SNP is causal is assumed to be equal for all SNPs. Sample size (N) ranges from 500–20,000, and the percent of trait variation explained by the causal variant, R², is 1%. SNPs are assumed to be equally correlated with magnitude ρ. The horizontal dotted line is for equal prior probabilities for SNPs, and the posterior probability approaches this line when the data have little information to distinguish causal from non-causal SNPs.

Genomic annotation

Genomic annotation that assigns biological function to DNA sequences can be informative about the likely function of SNPs selected by fine-mapping analyses, and can aid prioritization of follow-up functional studies. Large-scale initiatives have increased publicly available resources, including Gene Ontology⁷⁵, GENCODE⁷⁶, ENCODE⁷⁷, FANTOM5⁷⁸, and the Roadmap Epigenomics Project⁷⁹. By integrating multiple datatypes for a variety of tissues and cell-types, current annotations provide functional context for approximately 80% of the human genome⁸⁰. Analyses of published GWAS findings have identified significant enrichment for functional annotations among complex trait associations^81–83, motivating the use of annotation to improve fine-mapping resolution. Annotations are generally categorized according to protein-coding and non-protein-coding.

Protein-coding annotation

Annotation for SNPs in genes that code for proteins focuses on their impact on the resulting protein structure. Examples of annotation include whether a SNP occurs in an exon, an intron, a splice site, or whether it is involved in alternative splicing. A large number of bioinformatics annotation methods are available to functionally characterize coding SNPs and provide impact scores that predict their deleterious effect^84,85. Although prediction accuracy can be low from individual methods, combining methods can lead to improved predictions, such as by the CADD⁸⁶ and REVEL⁸⁷ methods.

Non-protein-coding annotation

The ENCODE project has shown that the genome is pervasively transcribed, and that the majority of bases are found in primary transcripts, including non-protein-coding transcripts⁸⁸. Genetic variation in non-coding regions is often involved in gene regulation. Some examples of non-coding annotation are promoters, enhancers, long non-coding RNA loci, transcription start sites, transcription factor binding sites, regulatory sequences, features of chromatin accessibility and histone modification patterns, and DNaseI hypersensitive sites. Variant impacts on putative transcription factor binding site (TFBS) motifs can be estimated by position weight matrices from databases such as TRANSFAC⁸⁹ and JASPAR⁹⁰. Annotation tools such as FIRE⁹¹, RegulomeDB⁹², and CADD⁸⁶ provide regulatory impact scores for non-coding SNPs by aggregating multiple evidence sources of functional importance.

Integrating annotation into fine-mapping

Ad-hoc review of SNP annotations is often applied to SNPs selected by fine-mapping analyses in order to identify patterns of annotation enrichment and prioritize candidates for functional validation. This subjective approach can be cumbersome and biased. Alternative methods can improve fine-mapping, such as using functional annotation to weight SNPs⁹³ in regression models, or extending Bayesian models to allow the prior probability that a SNP is causal to depend on annotation (see Supplementary information S1 (box))^57,94–97. Advantages of Bayesian methods are that the weights given to functional annotation are inferred from the data, and jointly mapping multiple regions simultaneously provides a way to share annotation information across different regions^57,95. Most methods allow for a relatively small number of annotation features, which requires screening each annotation one at a time in order to select a subset for a final model. An alternative approach that incorporates automatic selection of annotations from a large number of features overcomes this limitation⁹⁴. Bayesian mapping software that allows use of annotation is highlighted in Table 1.

The broad impact of the use of annotation on fine-mapping is yet unknown. By simulations, Van de Brunt et al.¹⁸ found that incorporating annotation into Bayesian prior probabilities gave modest benefit for fine-mapping, by increasing the frequency of small credible sets (e.g., less than 10 SNPs) from 27% without annotation to 36% with annotation. In real applications of fine-mapping four blood lipid traits, the 90% credible set size reduced from an average of 17.5 SNPs without use of annotation to 13.5 SNPs with use of annotation⁵⁷. When using a Bayesian method to fine-map three diseases in the Welcome Trust Case Control Consortium, very few SNPs in the credible sets were found to have annotated functions⁵⁰. So, use of annotation information can be limiting from two angles: first, incorporation of annotation into prior probabilities has limited impact on well-powered studies and second, current understanding of broad genomic function may be too limiting to accurately improve prior probabilities of causation. Conversely, annotation might help when association signals are at best moderate, or in regions of high LD, when there are multiple causal SNPs in a region, or when different regions share enrichment for specific annotation features.

Integrating GWAS with gene expression

More than 90% of trait-associated alleles discovered by GWAS map to non-coding regions, with strong evidence of enrichment for regulatory elements, such as enhancers, promoters, insulators, and silencers⁸¹. Furthermore, SNPs associated with complex traits are significantly more likely to be expression quantitative trait loci [G] (eQTLs) than other SNPs on genotype arrays with the same allele frequencies⁹⁸. This suggests that SNPs discovered by GWAS influence the amount of expression of nearby genes, and this altered expression ultimately influences the trait.

Statistical methods have been developed to integrate eQTL data with GWAS data to quantify the evidence of a causal pathway from SNP to gene-expression to a complex trait. The intermediate variable, mRNA, is the mediator between a SNP and a trait. One approach to test a causal pathway is by a causal inference test ⁹⁹, with small p-values inferring causality. Alternative Bayesian approaches focus on the posterior probability that a single SNP is causally related to both mRNA level and the trait ^100,101. Mendelian randomization is yet another approach that can be used to distinguish whether a single SNP influences both gene expression and the trait, versus whether separate SNPs in LD influence gene expression and the trait¹⁰². Details of these various approaches are provided in Supplementary information S1 (box).

A critical issue for integrating eQTL and GWAS results is the type of tissue for which the expression was measured. Complex diseases often result from dysfunction of multiple tissues or cell types, and the expression of genes varies widely across different types of tissues. Selecting relevant tissue types for a given disease process or complex trait can be a substantial challenge. Numerous public resources facilitate exploring gene expression in different tissues, such as the Genotype-Tissue Expression (GTEx) project, which includes genotypes, gene expression, and histological and clinical data for 449 human donors across 42 distinct tissues¹⁰³.

Conclusions

Fine-mapping efforts have made considerable advancements to refine the most likely genetic variants discovered by large-scale genetic association studies of complex traits. We reviewed a variety of analytical methods, with the more sophisticated and relevant methods based on Bayesian fine-mapping. A common underlying basis of all methods is LD between measured SNPs and causal variants that makes fine-mapping feasible, as well as challenging. Although the details of a particular study will determine the success of fine-mapping, general guidelines for evaluating the robustness of fine-mapping efforts are provided in Box 2. Most of our Review discussed SNPs. Other types of genetic variants can be analyzed with similar strategies, such as small insertions or deletions (indels) analyzed as binary variables. Currently, there are few general methods to incorporate large structural variants into GWAS fine-mapping. Yet, germline structural rearrangements have helped to discover simple Mendelian disease genes, such as partial deletion of chromosome 15 leading to discovery of the gene UBE3A that causes Angelman syndrome¹⁰⁴, or a 1.5Mb inversion on chromosome 17q12 leading to renal cysts and diabetes syndrome (RCAD), an autosomal dominant disorder ¹⁰⁵. Genetic variants with more than two alleles would require extension of current methods. For example, the human leukocyte antigen (HLA) locus on chromosome 6 is highly polymorphic and is involved with immune response and multiple diseases. This region has unique fine-mapping challenges, some of which can capitalize on GWAS data (see Supplementary information S1 (box)).

Box 2. Guidelines for evaluating fine-mapping.

The goal of fine-mapping is to determine which variants in a genomic region are most likely to be causally related to a trait after accounting for how the variants in the region are correlated. One challenge with Bayesian fine-mapping can be that the output credible sets contain a large number of variants. A way to reduce the number of putative causal variants is improved use of annotation, perhaps by careful selection of relevant cell-types for gene regulation annotation. Another way is to increase sample size. With large samples, Bayesian fine-mapping can sometimes result in a credible set of just a few variants, or perhaps a single variant. To gain confidence in fine-mapping results, it is worthwhile to evaluate the robustness of the results. Some guidelines for evaluating robustness are given below.

• What is the spread of the posterior inclusion probability (PIP) values for the variants in a credible set? If the PIPs are similar for multiple variants in a credible set, it can be worthwhile to view the correlation among the variants, and the effect sizes of the variants with effects of variants adjusted for each other. Large correlations among variants with similar effect sizes can suggest that it is not possible to distinguish among the variants with the available sample.

• When using summary statistics and a reference panel to estimate the SNP correlations, how well does the reference panel match the study sample? When possible, it is worthwhile to compare the correlations among the variants in the study sample with the correlations in the reference panel. Large differences between study sample and reference panel warrant further fine-mapping analyses with the correlations obtained by the study sample. When correlations among SNPs from the study sample are not available, comparison of allele frequencies between reference panel and study sample can sometimes reveal problems, such as large differences is allele frequencies.

• Because highly correlated SNPs can make fine-mapping difficult, sometimes compromising numerical computations, it is worthwhile to examine the correlations among the SNPs chosen based on fine-mapping. High correlations (e.g., more than 0.98) might warrant more careful scrutiny.

• Different software for fine-mapping make different assumptions, and the computational methods can be implemented differently. To evaluate the robustness of a finding, it can sometimes be worthwhile to compare results across different software packages. Consistent results can improve confidence in the fine-mapping findings. However, inconsistent results can be caused by multiple factors, including different modelling assumptions, rounding errors, or differences in stochastic search methods. Hence, comparison of results across different software packages can be useful, but expertise in the software is required in order to give adequate interpretation of results.

• Trans-ethnic fine-mapping assumes that the set of causal SNPs are the same for all populations, but accounts for differences in effect sizes across populations. For this reason, it can be worthwhile to evaluate the estimated effect sizes of the SNPs selected by fine-mapping to determine if just one, or a few, of several populations have effect sizes that dominate the fine-mapping.

As fine-mapping efforts proceed, an important consideration is the expected level of resolution. Using simulations that closely align with genomic structure of the UK 10,000 Genomes (UK10K) sample of 3,642 unrelated subjects of European ancestry, Wu et al.¹⁰⁶ found that at least 80% of common variants identified in published GWAS that used imputed data were within 33.5 kb of causal variants. This provides optimism for fine-mapping GWAS results when using the study designs and computational methods discussed in this Review. Sharing of data in large meta-analyses, and improved genomic annotation, will probably improve resolution.

The frequency of variants has a large impact on the success of fine-mapping by statistical methods. Wu et al.¹⁰⁶ found that rare untyped causal variants (minor allele frequency less than 0.01) are unlikely to map to a common variant in GWAS, whether using imputed data or whole-genome sequencing. Less-common variants tend to have lower levels of LD with other variants, making it challenging to impute less-common variants by statistical methods. But, low levels of LD can be advantageous for fine mapping when the variants are accurately genotyped or imputed and a study has high power to detect associations with single variants. Whole-exome sequencing and whole-genome sequencing open new avenues to discover rare variants. A challenge of these types of sequencing studies is the very large sample size (e.g., approximately 100,000 subjects) needed to discover regions that harbour rare causal variants for complex traits¹⁰⁷. Furthermore, the statistical methods for rare-variant associations with a trait do not focus on single rare variants, but rather evaluate an entire region¹⁰⁸. So, the initial discovery of a region provides little evidence of specific variants that are likely to be causal. Nonetheless, whole-genome sequencing can be informative for fine-mapping rare variants, but in this situation various sources of annotation of variants will be key to success¹⁰⁹. Alternative approaches that combine functional assay results with computational prediction of function¹¹⁰ might prove useful for fine-mapping, albeit with the requirement of functional assays developed for each specific region of interest.

Our understanding of the genetic basis of human disease has evolved from single major genes influencing rare Mendelian disorders to multiple genes — polygenic — influencing common complex traits. Future fine-mapping challenges will face complex traits driven by a large number of variants with small effects, possibly based on a genetic architecture of regulatory networks composed of a small number of core genes that directly affect a trait, but with a large number of genes outside the core that indirectly affect the trait — an omnigenic model¹¹¹. Understanding the genetic architecture of regulatory networks offers new opportunities to integrate this information into future fine-mapping strategies.

Online summary (Key Points).

• Genome-wide association studies of complex traits can identify multiple associated loci, each represented by one or more single-nucleotide polymorphisms (SNPs) with small p-values. An important next step to understanding the genetic contributions to a trait is identifying which SNP(s) are likely to be truly causal at a given locus.

• A major challenge in identifying underlying causal SNPs is the presence of linkage disequilibrium (LD), which can lead to highly correlated association results and multiple significant SNPs at a locus of interest. Fine-mapping methods aid this process by selecting and prioritizing variants most likely responsible for complex traits.

• A variety of computational fine-mapping approaches are reviewed, including heuristic, penalized models, and Bayesian methods. Bayesian methods are highlighted because of their flexibility and benefits.

• The main factors that influence the performance of Bayesian fine-mapping are quantified and discussed, including the number of causal variants in a region, the size of the effects of the variants on a trait, the SNP density, the local LD structure, and the sample size.

• Fine-mapping can be improved by further data integration, such as combining summary statistics from multiple cohorts to increases sample size, trans-ethic studies that capitalize on differences in the structure of linkage disequilibrium, use of genomic annotation, and integrated analysis of gene expression data with genetic markers and traits.

Glossary

Genome-wide association studies (GWAS)

Scans of genetic markers, typically single-nucleotide polymorphisms (SNPs), across DNA of many subjects to find variants statistically associated with a complex trait.

Complex traits

Either quantitative traits (e.g., blood pressure, height) or common diseases (e.g., major cancers) that are caused by many genetic and environmental factors working together, each having a relatively small effect and few if any being absolutely required for disease to occur.

Tag-SNPs

SNPs that are sufficiently correlated with neighbouring SNPs such that the tag-SNP serves as a surrogate for unmeasured SNPs.

Linkage disequilibrium (LD)

Non-random association of alleles at different loci on a haplotype in a given population. LD is key to fine-mapping, because coinheritance without recombination of alleles from different variants implies that the variants are proximal on the same chromosome.

Causal variants

Genetic variants that mechanistically contribute to diseases or quantitative traits, but are not fully penetrant in the sense that the variant may not be a sufficient cause in isolation.

Fine-mapping

To refine the genomic localization of causal variants by the use of statistical, bioinformatic or functional methods.

Penalized regression

A way to estimate regression coefficients by maximizing the log-likelihood of the data while placing a penalty that constrains the size of the regression coefficients, shrinking small coefficients toward zero, sometimes exactly to zero. Although this causes coefficient estimates to be biased, it improves the overall prediction of the model by decreasing the variance of the coefficient estimates.

Summary statistics

Measures of statistical association between a trait and one or more single-nucleotide polymorphisms (SNPs) that summarize the size of effects of the SNPs on the trait, the variances of the effect sizes, and how the effect sizes are correlated among themselves. For case–control studies, summary statistics include the estimated log-odds ratios from logistic regression, the variances of the log-odds ratios, and the correlations among the log-odds ratios.

Trans-ethnic

Genetic association study including subjects from more than one ethnic background.

Statistical power

The probability of correctly rejecting a null hypothesis of no statistical association between a single-nucleotide polymorphisms (SNP) and a trait when in truth a statistical association exists. Power depends on the magnitude of the SNP effect, the sample size, and the p-value threshold for deciding statistical significance.

Haplotype

A combination of alleles found on the same chromosome.

Haplotype block

A set of highly associated alleles on a chromosome that tend to be inherited together.

Genotype imputation

A method for estimating (‘imputing’) the unobserved genotypes of study subjects, both for individuals with missing or unreliable genotypes at a genotyped single-nucleotide polymorphism (SNP) and for all individuals at an ungenotyped SNP.

Recombination hot-spots

Genomic regions where the rate of recombination is much higher than neutral expectation.

Cross-validation

A technique to build a prediction model by randomly partitioning the sample into a training set to train the model (e.g., determine which single-nucleotide polymorphisms (SNPs) to include in a model), and a test set to measure its predictive performance (e.g., average squared prediction error). It is common to split the original sample into 10 equal size subsamples, use 9 to train and 1 to test, and repeat this process 10 times such that each of the 10 subsamples is used as a test sample, and then average the predictive performance over the 10 training subsamples.

Prior probability

In Bayesian probability theory, the probability distribution assigned to parameters of interest, specified to represent prior knowledge of their values before observing the data.

Posterior probability

In Bayesian probability theory, the updated probability distribution of parameters of interest, conditional on the observed data.

Posterior inclusion probability (PIP)

The marginal probability that a single-nucleotide polymorphism (SNP) is included in any causal model, conditional on the observed data, thereby providing weight of evidence that a SNP should be included as potentially causative.

Expression quantitative trait loci (eQTLs)

Genomic regions that harbour one or more nucleotide variants that influence the amount of expression of a gene.

Type-I error

(Also known as false-positive rate). The probability of incorrectly rejecting the null hypothesis of no association between a SNP and a trait, thereby falsely concluding a true association.

Multiple testing correction

When testing more than one statistical association, the probability of declaring at least one significant result increases as the number of statistical tests increases. If each of m independent statistical tests uses p-value<α to declare significance, then the chance that at least one of the m tests is found to be significant is approximately mα. Multiple testing correction maintains the overall chance of declaring at least one significant result by using more stringent p-value thresholds for each association tested. The Bonferroni correction uses p-value<α/m to test each association.

Biographies

Schaid Biosketch:

Daniel Schaid is the Curtis L. Carlson Professor of Genomics Research in the Division of Biomedical Statistics and Informatics at the Mayo Clinic in Rochester, Minnesota, USA. His research focuses on the development of statistical and computational methods for genetic analyses, and collaborations on genetic epidemology of complex diseases.

Daniel Schaid’s home page:

http://www.mayo.edu/research/labs/statistical-genetics-genetic-epidemiology

Chen Biosketch

Wenan Chen is a research scientist in the Department of Computational Biology at the St. Jude Children’s Hospital, Memphis, Tennessee, USA. His research focuses on the development of statistical and computational methods for genetic and genomic data analyses, especially those related to pediatric diseases.

Larson Biosketch

Nicholas Larson is an Assistant Professor of Biostatistics in the Division of Biomedical Statistics and Informatics at the Mayo Clinic in Rochester, Minnesota, USA. His research interests include statistical methods for genetic association studies, next-generation sequencing data analysis, and multi-omics data integration.