A Portable Structural Analysis Library for Reaction Networks

Abstract

The topology of a reaction network can have a significant influence on the network’s dynamical properties. Such influences can include constraints on network flows and concentration changes or more insidiously result in the emergence of feedback loops. These effects are due entirely to mass constraints imposed by the network configuration and are important considerations before any dynamical analysis is made. Most established simulation software tools usually carry out some kind of structural analysis of a network before any attempt is made at dynamic simulation. In this paper, we describe a portable software library, libStructural, that can carry out a variety of popular structural analyses that includes conservation analysis, flux dependency analysis and enumerating elementary modes. The library employs robust algorithms that allow it to be used on large networks with more than a two thousand nodes. The library accepts either a raw or fully labeled stoichiometry matrix or models written in SBML format. The software is written in standard C/C++ and comes with extensive on-line documentation and a test suite. The software is available for Windows, Mac OS X, and can be compiled easily on any Linux operating system. A language binding for Python is also available through the pip package manager making it simple to install on any standard Python distribution. The bulk of the source code is licensed under the open source BSD license with other parts using as either the MIT license or more simply public domain. All source is availle on GitHub (https://github.com/sys-bio/Libstructural).

Background

One of the most fundamental processes in living organisms is the chemical reaction where molecules combine, decompose, change configuration or exchange molecular subunits. A network of chemical reactions will obey mass-conservation resulting in properties of the network that are independent of the underlying reaction kinetics. In this paper, we describe a new portable software library that provides many facilities for analyzing the topological properties of reaction networks as a result of mass-conservation.

When describing multiple reactions in a network, it is convenient to represent the stoichiometric coefficients in a compact form called the stoichiometry matrix, N [16]. This matrix is a m row by n column matrix where m is the number of species and n the number of reactions. The columns of the stoichiometry matrix correspond to the distinct chemical reactions in the network, the rows to the molecular species, one row per species. The intersection of a row and column in the matrix indicates the stoichiometric coefficient.

The stoichiometry matrix represents the connectivity of the network and contains important information on the network’s structural characteristics. These characteristics fall into two groups, relationships among the species as indicated by dependencies in the rows of the stoichiometry matrix and relationships among the reaction rates due to dependencies among the columns [21]. In this paper, we will describe a software library called libStructural that provides a wide variety of functions to analyze both row and column dependences in a stoichiometry matrix. libStructural is not concerned with with constraint-based modeling [2] or metabolic flux analysis [13]. Instead it focuses on the structure of the stoichiometry matrix.

Moiety Conservation Laws

One of the characteristics of biological network models is the conservation of certain molecular subgroups, termed moieties [17]. A typical example of a conserved group in a model is the conservation of the adenine nucleotide moiety, i.e. the total amount of ATP, ADP, and AMP is constant during the evolution of the model.

Determining the conservation laws is important for several reasons. One practical advantage is that the system equations in the form of ordinary or stochastic differential equations can be reduced in size thus making numerical analysis more efficient. This fact is exploited in many modern modeling platforms including but not limited to SBW[20], Copasi[7], PySCeS[14], VCell[11], JWS Online [15], libRoadRunner [26], and the SB Toolbox [23]. A recent review of software provision in this area can be found in Dandekar [4]. In addition to reducing the size of the model, reduction of the number of differential equations means that the model’s Jacobian matrix is non-singular [21], an important requirement for a number of numerical methods including steady-state analysis and bifurcation analysis. The conservation laws are also important for theoretical reasons because a non-singular Jacobian is required for metabolic control analysis, stability analysis and frequency analysis [9]. Finally, conservation laws have very practical implications for perturbation studies and targeted gene knockouts [5]. In such circumstances, the conservation laws provide hard limits to how species levels can change, at least over the time scale of the conservation law. The conservation relationships can also lead to implicit regulatory effects in a network as exemplified by the work of Markevich [12].

The libStructural library supports the computation of L, L₀, and Γ matrices [17]. In addition, the library will reorder the stoichiometry matrix rows including row labels as appropriate.

Steady-State Flux Constraints

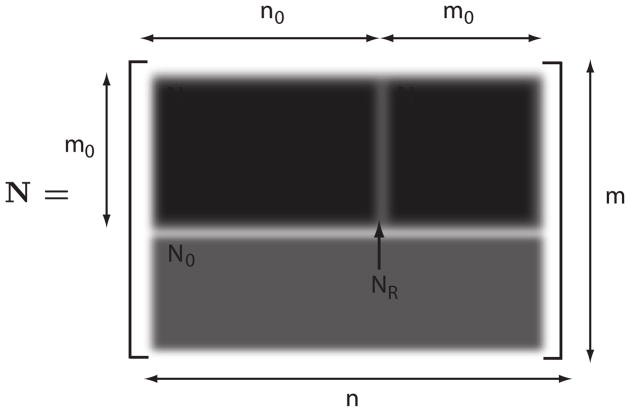
Whereas the rows of the stoichiometry matrix indicate dependencies among the species, the columns of the stoichiometry matrix indicate dependencies among the reaction rates [29]. The libStructural library supports the computation of K, N_DC, and N_IC matrices [17]. In addition, the library will reorder the stoichiometry matrix columns including column labels as appropriate. Figure 1 summarizes the partitioning of the matrix into the various subdivisions.

Figure 1.

Partitioned Reordered Stoichiometry Matrix: n = number of reactions; m = number of species; N_DC = partition of linearly dependent columns; N_IC = partition of linearly independent columns; N_R = reduced stoichiometry matrix; N₀ partition of linearly dependent rows.

Elementary Modes

Elementary modes [30] are the simplest pathways within a metabolic network that can sustain a steady-state and at the same time are thermodynamically feasible [1]. Depending on the size of the metabolic network, the number of elementary modes can range from no modes to billions of modes. The full set of elementary modes represents the complete metabolic potential of a given metabolic network and as a result is of interest to the metabolic analysis and engineering communities.

The libStructural library computes elementary modes via a refactored Metatool component [10] and includes both integer and double variants as well as a refactored gEFM library [27].

Results

Software Implementation

The core library for libStructural was originally developed by Frank Bergmann. With the development of the C/C++ version of libRoadRunner, libStructural was subsequently integrated into libRoadRunner [26]. In this paper, we describe the separate and reusable libStructural library.

The core of libStructural is written in ISO C/C++ to achieve maximum portability and interoperability. The software can be used on Windows, Mac OS X, and Linux operating systems. Network models can be supplied either directly as a raw stoichiometry matrix or indirectly as an SBML model [8]. For SBML support we use the libSBML library [3]. In order to maintain information on the row and column reorderings during the calculations, all row and columns of matrices can be labeled. The library relies heavily on LAPACK (http://www.netlib.org/lapack/), a standard library for linear algebra that is used to carry out householder reflections for the QR factorization [6].

The library itself is split into two parts. One part is used to wrap and expose certain LAPACK functions and to implement other commonly used linear algebra results not directly supported by LAPACK. These include methods that can compute orthonormal null space vectors or generate the reduced echelon forms using Gauss-Jordan matrix reduction. The second part implements the stoichiometric network specific methods. These include conservation analysis such as computing the link and gamma matrices (conservation matrix), returning the reordered row stoichiometry matrix and total amounts in each conservation law. In addition, the columns of the stoichiometric matrix are also analyzed to generate the independent and dependent fluxes, including the K matrix. Documentation is provided through readthedocs (https://libstructural.readthedocs.io). The source code is licensed under a combination of the modified BSD license, MIT (gEFM), and public domain ( libMetatool ).

For computing elementary modes there are a wide variety of published software tools. Rather than write our own we decided to reuse existing software. We examined a wide variety of existing tools, and we found only two, Meta-tool [10] and gEFM [27] that could be easily reused within our C/C++/Python framework.

Metatool 4.3 is written in standard C and has a liberal open license. It is therefore very easy to implement across different computing platforms. We refactored the code to convert Metatool 4.3 into a reusable library we call libMetatool. This allows Metatool to be linked to any programming language. The refactoring was done such that libMetatool can be used independently of libStructural. The one major change to Metatool when refactoring was to use 64-bit integer types for all calculations. This was done to improve the numerical stability of the algorithms used by the integer version Metatool when dealing with large models. Since the original Metatool source code is in the public domain, the refactored Metatool source code is similarly unrestricted. In order to deal with models with fractional stoichiometries, we also distribute the double version of Metatool and a refactored gEFM.

We also incorporated gEFM as a library which is a more modern distribution that uses a completely different algorithm to Metatool. The code was refactored by adding an API (Application Programming Interface) and improved error handling and memory protection. The addition of gEFM allows comparisons to be made between Metatool and gEFM. For gEFM, we also provide a copy results to file method that can be used for analyzing large models. This was to avoid returning very large arrays directly to the Python console from gEFM. gEFM can be accessed via the Python call getgElementaryModes().

In addition to the C/C++ library, we also created Python bindings to allow users access to the functionality of libStructural via Python. We used the SWIG toolkit (http://www.swig.org/) to generate the Python bindings and have deployed the Python enabled libStructural via standard pip packaging.

Applications and Examples

Branched Metabolic Network

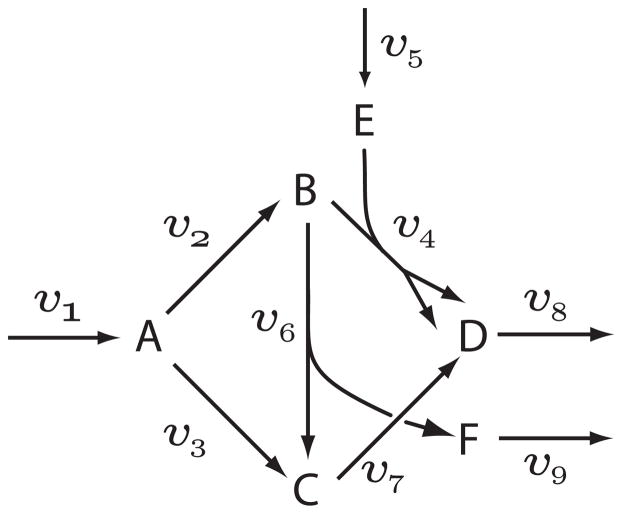
Consider a metabolic network with nine reactions and six floating species shown in Figure 2. The model was described using the Antimony syntax [25] which was then exported as SBML.

Figure 2.

Branched network

An SBML model can be loaded by calling the loadSBMLFromFile function. By default, the library will apply QR factorization to the model.

   ≫> import structural
   ≫> ls = structural.Libstructural()
   ≫> ls.loadSBMLFromFile(“branched_network.xml”)

Models can also be conveniently loaded using the Antimony syntax [25] as shown below:

   import tellurium as te
   import structural
   r = te.loada(”””
    $Xo -> x; k1*Xo;
    x -> $X1; k2*x;
    Xo = 1; k1 = 0.5; k2 = 0.15;
   ”””)
   ls = structural.LibStructural()
   ls.loadSBMLFromString (r.getSBML())
   print ls.getStoichiometryMatrix()

After loading a model, a summary of the analysis can be obtained using the getSummary method as shown below:

   ≫> ls.getSummary()
   --------------------------------------------------------------
   STRUCTURAL ANALYSIS MODULE : Results
   --------------------------------------------------------------
   Size of Stochiometric Matrix: 6 x 9 (Rank is 6)
   Nonzero entries in Stochiometric Matrix: 16 (29.6296% full)
   Independent Species (6) :
   D, A, C, F, E, B
   Dependent Species : NONE
   L0 : There are no dependencies. L0 is an EMPTY matrix
   Conserved Entities: NONE

Specific information can be obtained by calling a variety of methods. For example, the stoichiometry matrix is obtained as follows:

   ≫>ls.getStoichiometryMatrix()
   array([[ 1., -1., -1., 0., 0., 0., 0., 0., 0.],
          [ 0., 1., 0., -1., 0., -1., 0., 0., 0.],
          [ 0., 0., 1., 0., 0., 1., -1., 0., 0.],
          [ 0., 0., 0., -1., 1., 0., 0., 0., 0.],
          [ 0., 0., 0., 2., 0., 0., 1., -1., 0.],
          [ 0., 0., 0., 0., 0., 1., 0., 0., -1.]])

The order of species and reactions in the rows and columns can be obtained using the methods getFloatingSpeciesIds and getReactionIds. At this stage, neither the rows or columns have been reordered into dependent and independent rows and columns. A call to getFullyReorderedStoichiometryMatrix will return a stoichiometry matrix where both rows and columns have been reordered:

   ≫>ls.getFullyReorderedStoichiometryMatrix()
   array([[ 1., -1., 0., 2., 0., 0., 0., 0., 0.],
          [ 0., 0., -1., 0., 0., -1., 0., 0., 1.],
          [-1., 0., 0., 0., 1., 1., 0., 0., 0.],
          [ 0., 0., 0., 0., 1., 0., 0., -1., 0.],
          [ 0., 0., 0., -1., 0., 0., 1., 0., 0.],
          [ 0., 0., 1., -1., -1., 0., 0., 0., 0.]])

The ordering of the rows and columns can be obtained by calling getFully-ReorderedStoichiometryMatrixIds. This returns two lists, the reordered row and column labels. Reordering of only the rows can be obtained by calling getReorderedStoichiometryMatrix.

The number of dependent and independent reaction rates can be obtained by calling getNumDepReactions and getNumIndReactions. In the case of the example model, these methods return 3 and 6 respectively. getDependent-ReactionIds and getIndependentReactionIds will return the ids of the specific reactions in each group. For example:

   ls.getDependentReactionIds()
   Out[24]: (’J7’, ’J8’, ’J2’)
   ≫>ls.getIndependentReactionIds()
   Out[25]: (’J4’, ’J6’, ’J3’, ’J5’, ’J9’, ’J1’)

In practical terms the fluxes through (’J4’, ’J6’, ’J3’, ’J5’, ’J9’, ’J1’) can be used to determine the remaining three fluxes: (’J7’, ’J8’, ’J2’). A full range of methods are available to extract any of the submatrices shown in Figure 1.

Network Containing Conserved Moieties

The model shown in Figure 3 illustrates a simple reaction network that contains two conserved moieties, S and E. These result in two conservation laws: S₁ + S₂ + ES and ES + E.

Figure 3.

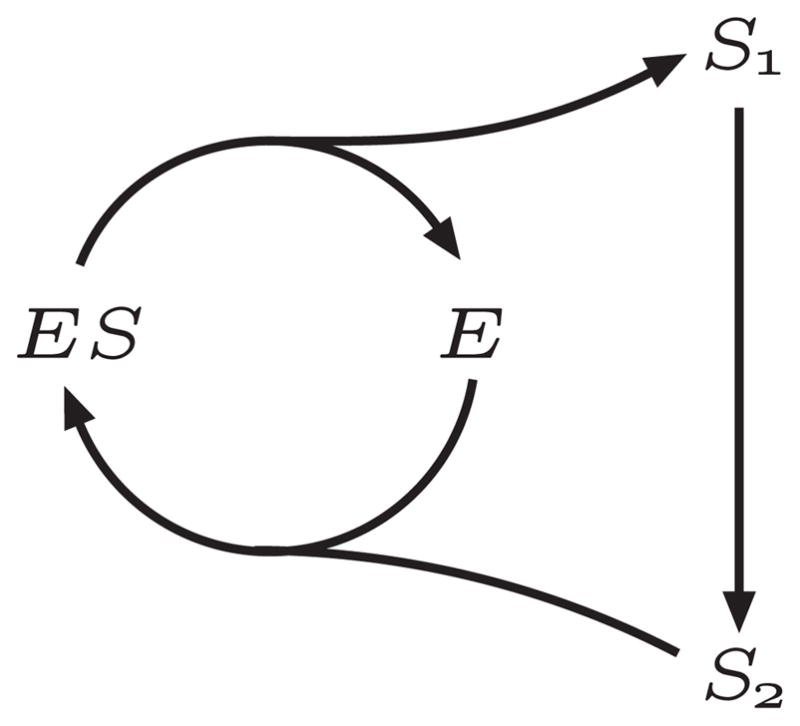
Network with Two Interlinked Conserved Moieties.

After loading the model, calling getSummary generates the following output:

   ≫ ls.getSummary()
   --------------------------------------------------------------
   STRUCTURAL ANALYSIS MODULE : Results
   --------------------------------------------------------------
   Size of Stochiometric Matrix: 4 x 3 (Rank is 2)
   Nonzero entries in Stochiometric Matrix: 8 (66.6667% full)
   Independent Species (2) :
   ES, S1
   Dependent Species (2) :
   E, S2
   L0 : There are 2 dependencies. L0 is a 2x2 matrix.
   Conserved Entities
   1: + ES + E
   2: + ES + S1 + S2

From the summary, we can see that there are two dependent rows (species) and two conserved entities. Thus, the conservation matrix (gamma, Γ) will have two rows.

   ≫>ls.getStoichiometryMatrix()
   array([[-1., 0., 1.],
          [ 1., -1., 0.],
          [ 1., 0., -1.],
          [ 0., 1., -1.]])
   ≫> ls.getGammaMatrix()
   array([[ 1., 0., 1., 0.],
          [ 1., 1., 0., 1.]])

In addition, it is possible to obtain the conserved sums and conserved laws of the network by calling getConservedLaws and getConservedSums respectively.

   ≫>ls.getConservedLaws()
   (’ + ES + E’, ’ + ES + S1 + S2’)
   ≫>ls.getInitialConditions()
   ((’ES’, 10.0), (’S1’, 10.0), (’E’, 10.0), (’S2’, 10.0))
   ≫> ls.getConservedSums()
   (20.0, 30.0)

The function getFullyReorderedStoichiometryMatrix divides the N_R matrix into N_IC and N_DC matrices as shown in Fig 2.

   ≫> ls.getFullyReorderedStoichiometryMatrix()
   array([[ 1., -1., 0.],
          [ 0., 1., -1.],
          [-1., 1., 0.],
          [-1., 0., 1.]])
   ≫>ls.getFullyReorderedNrMatrix()
   array([[ 1., -1., 0.],
          [ 0., 1., -1.]])
   ≫> ls.getNICMatrix()
   array([[-1., 0.],
          [ 1., -1.]])
   ≫> ls.getNDCMatrix()
   array([[ 1.],
          [ 0.]])

Calculating elementary modes

To illustrate the evaluation of the elementary modes, consider a simple branched model. The representation of this model using Antimony syntax makes it easy to specify whether a given reaction is reversible or not. Reactions that are irreversible are indicated by => while reactions that are reversible are indicated with ->.

        J1: $Xo => A; v;   J2: A => B; v;
        J3: A => C; v;     J4: B + E => 2 D; v;
        J5: $X1 => E; v;   J6: B => C + F; v;
        J7: C => D; v;     J8: D => $X2; v;
        J9: F => $X3; v;   v = 0;

If all reactions are irreversible, then the model admits only three elementary models. If all reactions are reversible then ten elementary models are possible (not shown). From the Antimony script, we can generate standard SBML which, as before, can be loaded into libStructural. Three elementary model methods are implemented, getElementaryModesInteger, getElementary-ModesDouble, and getgElementaryModes. The first two call Metatool integer and double respectively and the last method calls gEFM. For example, callling the getElementaryModesInteger function returns the following three elementary modes.

   ≫> ls.getElementaryModesInteger()
   [[ 1. 1. 0. 1. 1. 0. 0. 2. 0.]
    [ 1. 0. 1. 0. 0. 0. 1. 1. 0.]
    [ 1. 1. 0. 0. 0. 1. 1. 1. 1.]]

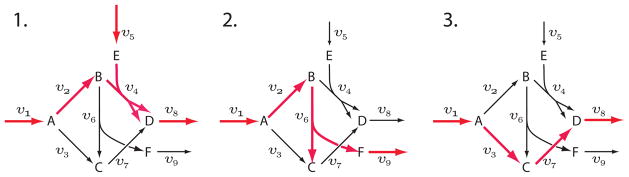
The elementary modes in the output are arranged in rows. The order of the columns in the output can be obtained by calling getReactionIds which returns the list of reaction names. To assist in visualizing the three modes, Figure 4 highlights the reactions involved in each of the modes. This shows there are three independent and thermodynamically feasible pathways in the network: 1) v₁ to v₉ via v₂ and v₄; 2) v₁ to v₈ via v₂ and v₆; and 3) v₁ to v₉ via v₃ and v₇. All possible thermodynamically feasible flux patterns can be obtained by linear combinations of these three.

Figure 4.

Three Elementary Modes in a Complex Pathway.

Availability

LibStructural is available either as source code or as pre-compiled modules for Windows and Mac OS X. The source code is available on GitHub (https://github.com/sys-bio/Libstructural). CMake (https://cmake.org/) configurations are supported to generate build systems for different compilers and platforms. SWIG (http://www.swig.org/) is necessary for generating Python wrappers. Extensive instructions on how to build libStructural are available at https://libstructural.readthedocs.io.

libStructural can be installed in Python via the Python packages manager pip. Support for Python 2.7 and 3.4+ is available and standard Python users should execute pip install libStructural at the command line. When using Tellurium [19], libStructural can be installed directly from the Python console via the installPackage function.

Methods

Details of the algorithms can be found in [24, 28]. Much of the analysis done in libStructural is based on Householder reflections [18] to compute the QR factorization of the stoichiometry matrix. The QR decomposition results in a very robust numerical scheme to extract the species and flux dependencies. We illustrate the approach using a number of large models obtained from the BiGG repository [22] (see http://bigg.ucsd.edu//). The results of these analyzes are shown in Table 1.

Table 1.

Results of analyzing a selection of large models from http://bigg.ucsd.edu/. Dep Rxns indicates the number of dependent reactions and Ind Rxns the number of independent reactions. sp is short-hand for species and rxn for reactions.

Model	# Conserved Moieties	# Dep Rxns	# Ind Rxns
RECON1 (3741 rxn, 2766 sp)	92	1067	2674
IJR904 (1975 rxn,761 sp)	18	332	743
IND750 (1266 rxn, 1059 sp)	77	284	982
iJO1366 (2583 rxn, 1805 sp)	39	817	1766
iNRG857 1313 (2735 rxn, 1311 sp)	60	852	1883
iYO844 (1250 rxn, 990 sp)	31	291	959
iYL1228 (2262 rxn, 1658 sp)	45	649	1613
STM v1 0 (2545 rxn, 1802 sp)	39	782	1763

Self-Test Routines

The library includes six tests to validate the conservation laws and the general integrity of the results. These tests need only be carried out for very large models where there the rare possibility of errors due to rounding errors. In such situations, the library tolerance setting can be reduced using the setTolerance method and the analysis and self-tests rerun.

Calling validateStructuralMatrices() returns a list of a true/false values or getTestSummary() which returns a string giving a more detailed account, for example, getTestSummary() will yield:

   Passed Test 1 : Gamma*N = 0 (Zero matrix)
   Passed Test 2 : Rank(N) using SVD (1) is same as m0 (1)
   Passed Test 3 : Rank(NR) using SVD (1) is same as m0 (1)
   Passed Test 4 : Rank(NR) using QR (1) is same as m0 (1)
   Passed Test 5 : L0 obtained with QR matches Q21*inv(Q11)
   Passed Test 6 : N*K = 0 (Zero matrix)

Tests for Elementary Modes

There are three tests we use to check that the software returns valid elementary modes. Due to the current state of understanding of elementary models, it is not possible to determine before-hand how many elementary modes to expect. Therefore it is not possible to know with certainty whether all elementary modes have been identified. This is particularly true for larger networks where the number of elementary modes can be extremely large. The tests we use include:

1. All elementary modes must satisfy Ne_i = 0.

2. For a given elementary mode, e_i, it must be true that:

   1. The null space of the submatrix of N that only involves the reactions of e_i is of dimension one and has no zero entries (elementarity).

   2. The elementary mode must be consistent with respect to the sign of the coefficient for irreversible reactions (thermodynamic correctness). That is, if a reaction is irreversible, its corresponding sign in e_i must be positive. A reversible reaction may be negative or positive.

The test file elementaryModes.py includes 30 models together with the required tests. All test files, documentation and source code can be obtained at https://github.com/sys-bio/Libstructural.