FIG. 2.

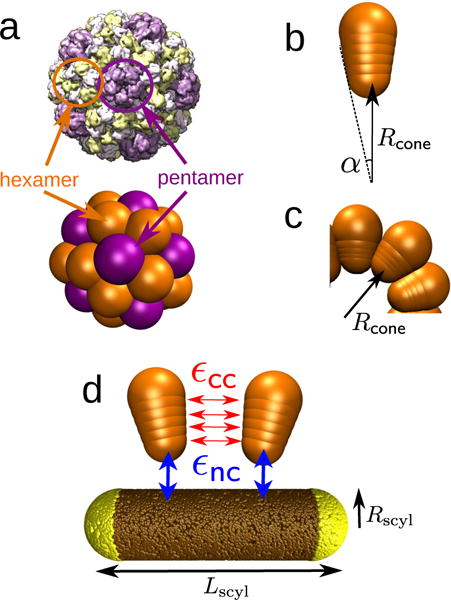
(a) Brome mosaic virus (BMV) capsid structure obtained from cyoEM (PDB ID: 3J7M) [79], compared with a capsid assembled from conical subunits in the absence of a nanoparticle. Each conical subunit represents a capsomer, and both pentamers (five neighbors, in purple) and hexamers (six neighbors, in orange) can be identified, showing icosahedral organization consistent with T=3 symmetry [22, 80]. (b,c) The cone angle α (b) sets the capsid spontaneous curvature radius R_cone (c), defined as the radial position of the capsomer bottom bead in the lowest energy capsid. (d) Capsomer model for R_cone = 9.5nm. Each of four interior beads (indices n = 1 … 4) interacts through a Morse potential of depth ε_cc with its counterparts in neighboring capsomers (red). The bottom capsomer bead experiences attractive interactions of strength ε_nc with the nanoparticle beads (blue). The equilibrium distance of the Morse potential between nanoparticle and capsomer beads, $r_{\text{eq}}^{\text{nc}}$, must be considered in the template curvature. The effective template radius is then given by $R_{\text{scyl}}^{\prime }=R_{\text{scyl}}+r_{\text{eq}}^{\text{nc}}$.