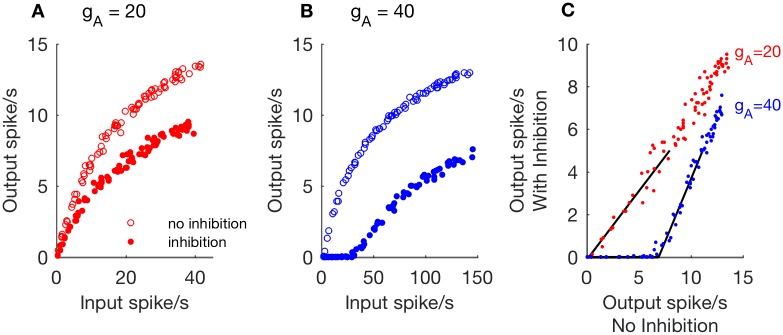
Fig 2. Examples of divisive and subtractive effects of inhibition in the one-compartment model.

A, B: Output firing rates as a function of excitatory input rate, computed from simulations without inhibition (empty circles, g_Syn,I = 0) and with inhibition (filled circles, g_Syn,I = 1 and r_I = 50 Hz). Excitatory synaptic strength is g_Syn,E = 0.5. In A: Divisive rescaling of the input/output relation with g_A = 20. In B: Subtractive shifting of the input/output relation with g_A = 40. C: Data from A and B are replotted with output firing rates in the absence of inhibition on the ordinate and output firing rates in the presence of inhibition on the abscissa. Threshold-linear functions are fit to simulation data (black lines). Rightward shift of threshold-linear function for g_A = 40 is characteristic of subtractive inhibition.