A biophysical modelling platform of the cochlear nucleus and other auditory circuits: from channels to networks

Abstract

Models of the auditory brainstem have been an invaluable tool for testing hypotheses about auditory information processing and for highlighting the most important gaps in the experimental literature. Due to the complexity of the auditory brainstem, and indeed most brain circuits, the dynamic behavior of the system may be difficult to predict without a detailed, biologically realistic computational model. Despite the sensitivity of models to their exact construction and parameters, most prior models of the cochlear nucleus have incorporated only a small subset of the known biological properties. This confounds the interpretation of modelling results and also limits the potential future uses of these models, which require a large effort to develop. To address these issues, we have developed a general purpose, biophysically detailed model of the cochlear nucleus for use both in testing hypotheses about cochlear nucleus function and also as an input to models of downstream auditory nuclei. The model implements conductance-based Hodgkin-Huxley representations of cells using a Python-based interface to the NEURON simulator. Our model incorporates most of the quantitatively characterized intrinsic cell properties, synaptic properties, and connectivity available in the literature, and also aims to reproduce the known response properties of the canonical cochlear nucleus cell types. Although we currently lack the empirical data to completely constrain this model, our intent is for the model to continue to incorporate new experimental results as they become available.

Introduction

The nervous system interprets and identifies objects in the acoustic environment using cellular substrates that are highly interconnected, non-linear, and time-dependent. These features endow the system with a diversity of complex and often unintuitive behaviors (Izhikevich, 2007; Rinzel and Huguet, 2013). Consequently, it can be difficult to predict the outcomes of specific manipulations, such as removing inhibition, at the cellular level, or the underlying causes of pathological conditions by simply extrapolating from the basal behavior of the system. However, computational approaches and modeling can help provide insights and generate predictions that can be experimentally tested, as well as provide support for the plausibility of existing interpretations of experimental results and underlying mechanisms. Here we describe a computational platform for investigating the behavior of neurons and neural circuits in the cochlear nuclear complex.

The cochlear nuclear complex (Osen, 1969) is composed of a large number of cell types. The principal cell classes (defined as cell types whose axons leave the cochlear nuclear complex) have been well studied both in vivo and in vitro. In particular, the intrinsic excitability (Bal and Oertel, 2001; Ferragamo et al., 1998; Golding et al., 1999; Hirsch and Oertel, 1988a; Hirsch and Oertel, 1988b; Kuo et al., 2012; Manis, 1990; Manis et al., 1994; Oertel, 1983; Oertel et al., 1990; Rodrigues and Oertel, 2006; Street and Manis, 2007; Zhang and Oertel, 1993a; Zhang and Oertel, 1993b), the ion channels that underlie the intrinsic excitability of the cells (Bal and Oertel, 2001; Cao and Oertel, 2011; Cao et al., 2007; Harasztosi et al., 1999; Kanold and Manis, 1999; Kim and Trussell, 2006; Manis and Marx, 1991; Manis et al., 2003; Rothman and Manis, 2003a; Rothman and Manis, 2003c; Rusznák et al., 1996; Rusznák et al., 1997), the kinetics of synaptic conductances (Gardner et al., 1999; Gardner et al., 2001; Harty and Manis, 1998; Kopp-Scheinpflug et al., 2002; Nerlich et al., 2014; Raman and Trussell, 1992; Raman et al., 1994; Xie and Manis, 2013; Xie and Manis, 2014) and the temporal dynamics of synaptic transmitter release (Kuo et al., 2012; Mancilla and Manis, 2009; Roberts and Trussell, 2010; Wang and Manis, 2008; Wang et al., 2010; Xie and Manis, 2013; Xie and Manis, 2017b; Yang and Xu-Friedman, 2008; Yang and Xu-Friedman, 2009) have been quantitatively described for several of the principal cell types. Connectivity amongst the cells within the territories of the cochlear nuclear complex is known qualitatively (Campagnola and Manis, 2014; Mancilla and Manis, 2009; Muniak and Ryugo, 2014; Munirathinam et al., 2004; Oertel et al., 1990; Ostapoff et al., 1999; Roberts and Trussell, 2010; Roberts et al., 2008; Wickesberg and Oertel, 1988; Wickesberg et al., 1991; Yaeger and Trussell, 2015; Yaeger and Trussell, 2016), and new methods are on the horizon to provide better quantitative measures of connections between identified neuronal classes (Deerinck et al., 2015; Denk and Horstmann, 2004; Holcomb et al., 2013; Joesch et al., 2016; Lees et al., 2017). The availability of computational representations for these cells and network components makes it feasible to build biophysically based models of the cells that can be used to test hypotheses and to perform a retrospective evaluation of the plausibility of particular interpretations of experimental results. Such detailed models can complement and extend simpler representations, such as those based on integrate-and-fire models of the neurons (Fontaine et al., 2013; Zhang and Carney, 2005). Furthermore, for some cell types, detailed morphological information is available that can be used to further refine the representations and explore the structure-function relationships of the neural circuits in more depth.

Many models of the cochlear nucleus neurons and circuits have been published previously (Arle and Kim, 1991a; Arle and Kim, 1991b; Banks and Sachs, 1991; Fernald, 1971; Ghoshal et al., 1992; Hancock and Voigt, 1999; Hewitt and Meddis, 1993; Hewitt and Meddis, 1995; Kalluri and Delgutte, 2003; Kanold and Manis, 2001; Kanold and Manis, 2005; Lai et al., 1994; McGinley et al., 2012; Nelson and Carney, 2004; Pressnitzer et al., 2001; Rothman and Manis, 2003a; Rothman et al., 1993; Rudnicki and Hemmert, 2017; Spencer et al., 2012; Wang and Sachs, 1995; Xie and Manis, 2013; Zhang and Oertel, 1993a; Zhang and Oertel, 1993b; Zheng and Voigt, 2006). Most of these models have generally been built with the explicit purpose of demonstrating the feasibility of a particular hypothesis or have focused on a single cell type or a limited portion of the circuit. Typically, such models only include the minimal set of components necessary to function, which raises the possibility that a more complete model might behave differently. Only a few models have included more complete representations of local circuits (Eager et al., 2004; Eriksson and Robert, 1999; Hancock and Voigt, 1999; Zheng and Voigt, 2006).

To facilitate the use of standardized model components, we have developed a platform for biophysically-based modeling of neurons and neural circuits in the auditory brainstem. In contrast to many previous modeling efforts, our platform is intended as a general-purpose, data-driven model that aims to incorporate many known biological constraints, provide flexibility for adding components as needed, and at the same time reproduce a broad set of known physiological functions. By building a model with constraints from a large set of biological mechanisms and functional parameters, we increase the likelihood that the model’s information processing capabilities will actually reflect those used in the brain. As we discuss the modeling platform and present simulation results, we will point out some major issues that arise in generating good models, and limitations of the data used to generate the models. We also provide examples of the model output and some usage cases.

Methods

A global overview of the structure of the CNModel platform is shown in Figure 1. The architecture consists of three primary layers. The lowest layer contains ion channels, presynaptic release mechanisms, and synaptic receptors. The next layer defines a set of cochlear nucleus cell types, which are implemented in Python as a set of rules describing the morphology, ion channel densities, and synaptic properties for each cell type. At the highest layer, we describe the distributions of cell properties across an entire population and the rules for connectivity between populations. This multi-layered approach allows complex models to be instantiated with little code, while still allowing fine-tuned control over properties at the lower layers. In addition, the platform includes a set of tests to ensure that the model output remains stable as we continue its development, and that it reproduces selected results from the literature.

Figure 1.

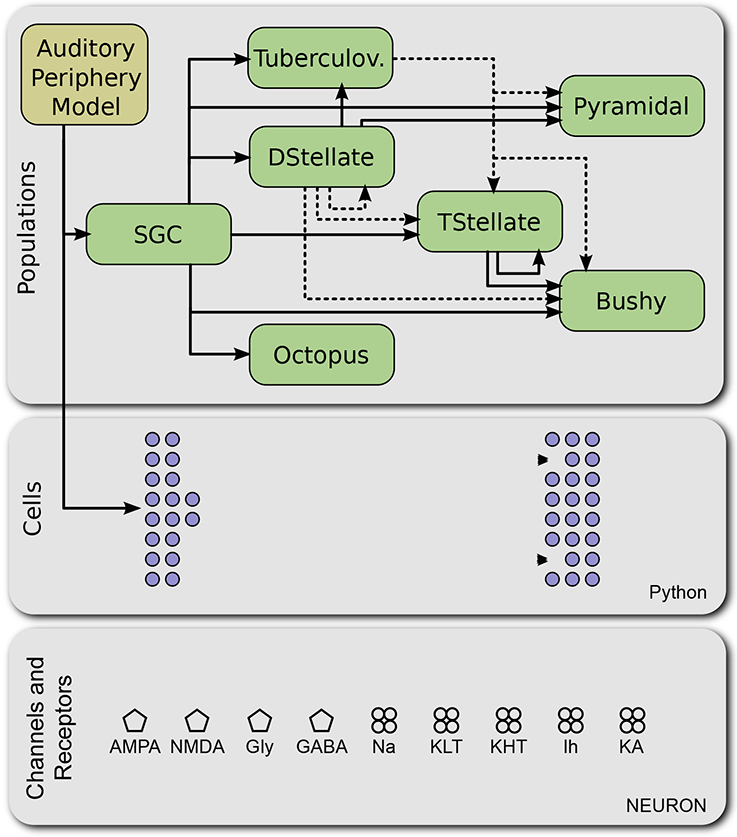
Architecture of CNModel. The modeling platform is divided according to conceptual levels and implementations. At the lowest level, the model includes specific mechanisms of ion channels, synaptic release mechanisms, and neurotransmitter receptors, implemented in NEURON (bottom container). At the next level, these components are combined to generate electrically excitable cells, as directed by a Cells class in Python (middle container). At the next level, Populations of cells can be combined into a circuit as specified in Python (top container). Excitatory connections are shown with solid lines; inhibitory connections are shown with dashed lines. An external auditory periphery model can be used to generate spike trains in spiral ganglion cells (SGC). Tuberculov.: Tuberculoventral cells.

Our platform is implemented in Python and builds on two existing simulation packages. The underlying computations use the NEURON engine (Hines and Carnevale, 1997; Hines and Carnevale, 2001) to simulate the non-linear and time-dependent current and voltage behavior of ion channels, to compute the current flows in complex neural arbors, and to simulate synaptic dynamics, transmitter release and receptors mechanisms at synapses. The platform also uses a Python implementation of the auditory periphery model of Zilany et al. (Rudnicki et al., 2015; Zilany et al., 2014; Zilany et al., 2009), to generate auditory nerve spike trains from sound stimuli.

Although CNModel is focused on the representation of neurons in the cochlear nucleus, the framework of the platform can be adapted to other cell types and synapses once appropriate measurements have been made.

Channels

At the lowest level, we provide a library of NEURON NMODL implementations of ion channels found in many brainstem neurons, as “generic” representations using Hodgkin-Huxley frameworks. These include well-established models of sodium, potassium, and calcium channels as well as some exploratory mechanisms. We also provide implementations of neurotransmitter receptors as state models based on various receptor models in the literature (Raman and Trussell, 1992), with kinetics tuned to match the kinetics of mammalian (primarily mouse) data (Xie and Manis, 2013). These mechanisms are based on experimental data to the extent that such data are available. The NEURON NMODL implementations (.mod files) are derived from both our work (Kanold and Manis, 2001; Liu et al., 2014; Rothman and Manis, 2003b) on channel kinetics, as well as from many published mechanisms that can be found in ModelDB (McDougal et al., 2017; Migliore et al., 2003) (www.senselab.med.yale.edu/ModelDB). In some cases, the mechanisms have been adjusted based on measurements from other published data (Bal and Oertel, 2000; Cao and Oertel, 2011; Cao et al., 2007; McGinley et al., 2012). Some published models from other labs have been adapted (for example, the mechanisms for cartwheel cells were adapted from a Purkinje cell model (Khaliq et al., 2003)) or modified to be consistent with our nomenclature.

Cells

At the next level (Figure 1, middle panel), we provide descriptions of several cell types in the cochlear nucleus. In CNModel, each cell type is represented as a Python class that defines the procedures for generating morphology, distributing ion channels across the membrane and setting their densities, and defining the properties of synapses. The cell type classes inherit most of their infrastructure from a base Cell class, which includes routines that manage and monitor the insertion of channels, determine the resting potential (zero current potential) for point models, provide stub routines for insertion of postsynaptic receptor mechanisms, set and verify the validity of the temperature for the simulation, and report on the channels and channel densities in different parts of the cells.

One instance of any of these cell type classes represents exactly one neuron. Cell classes may be further divided into a class hierarchy. For example, the base DStellate class is further inherited by DStellateRothman and DStellateEager classes that each implement different D-stellate models that have been published previously (Eager et al., 2004; Rothman and Manis, 2003b). Most cells in the library are “standard” models based on published data for bushy, T-stellate, octopus, and dorsal cochlear nucleus pyramidal cells. Ad-hoc models are included for spiral ganglion cells (SGCs) with either apical or basal-middle-like Ih currents, D-stellate cells, tuberculoventral cells, cartwheel cells, and medial superior olive principal cells. These models are constrained to match input resistances and firing patterns in published studies in mouse and guinea pig.

For most models, there are two possible levels of morphological description. The first is the “point” cell (really a sphere or a single isopotential equivalent cylinder in NEURON), which is useful for testing the functional importance of mechanisms and the consequences of varying their parameters. Many of the “standard” models are based on such point models because of their tractability and small parameter space. Point cell models include standardized parameter sets for published variants of the point models, and some ad-hoc parameter sets used to explore variations in mechanisms. The second level of description is to incorporate the cell morphology. Morphologically-defined models are instantiated in the same way as a point model, but use information from an imported HOC (the scripting language used by NEURON) or SWC file (Cannon et al., 1998) to establish a cable-based morphological scaffold. The morphology may be formalized as an approximate representation (“stick”, or procedurally-generated cells), or it may be more realistic, by using reconstructions from filled cells or serial block face electron microscopy.

After the cell morphology is established, the membrane is “decorated” with channels using a ChannelDecorator object, which specifies the density (or density gradient) of different kinds of channels in each of the compartments of the cell. Each cell type class may implement its own ChannelDecorator to customize the intrinsic membrane properties for cells created from that class. Adding dendritic trees and axons creates an additional complexity, however, in that we rarely know the actual density and distribution of channels in cell compartments other than the soma. Thus, this requires some educated guesses, and exploration of parameter spaces, and presents a challenge for future measurements. The platform is designed to allow such distributions to be explored in a limited way.

Synapses

Every synapse in CNModel is represented by an instance of the Synapse class, which encapsulates the details of presynaptic spike detection, neurotransmitter release, and postsynaptic receptor behavior. Synapses are created by calling the connect method of the presynaptic cell with the postsynaptic cell as an argument. Each cell type class may customize the routines that are used during synapse construction to determine the presynaptic release and postsynaptic response properties.

The following Python example demonstrates how to create a single spiral ganglion cell that is synaptically connected to a bushy cell:

from cnmodel.cells import Bushy, SGC
# Create a spiral ganglion cell and force it to spike four times.
sgc = SGC.create(model=‘dummy’, species=‘mouse’)
sgc.set_spiketrain([51.0, 54.5, 60.0, 68.1])
# Create a single bushy cell.
bushy = Bushy.create(species=‘mouse’)
# Create a synapse from the spiral ganglion cell
# to the bushy cell. The default creates a multisite synapse.
sgc.connect(bushy)

CNModel implements two different types of synapse. The first is a simple synapse based on the Exp2Syn function in NEURON, with an adjustable amplitude and double-exponential rise/fall kinetics. This synapse is efficient to compute, simple to configure, and should be used for most testing. The second synapse implementation is a physiologically detailed model (originally based on the work of (Graham et al., 2001)) that includes stochastic release from multiple release zones per terminal, synaptic cleft diffusion, and detailed receptor mechanisms as described previously (Xie and Manis, 2013). This synapse is computationally expensive but may capture important behaviors, including rate-dependent facilitation and depression of release, that are not available with the simpler implementation. The receptor mechanisms implemented in CNModel include the kinetic description of rapidly desensitizing AMPA receptors (Raman and Trussell, 1992) as modified for mouse bushy cells (Xie and Manis, 2013). The mechanism has been augmented by including polyamine block typical of GluR2-lacking receptors (Washburn et al., 1997; Woodhull, 1973)). Additional receptor types are glycine receptors, which are based on different mechanistic implementations that have been tuned against data from mouse cochlear nucleus neurons (Xie and Manis, 2013) and NMDA receptors (Kampa et al., 2004). Each receptor mechanism has its own defined equilibrium potential, which is implemented in the NEURON mechanism for the receptor, and can be set from the Synapse class.

Populations

The Population class is used to instantiate groups of cells and establish their connectivity (Figure 1, top box). Each cell type class has a corresponding Population class that implements the rules that determine how cell properties are distributed across the population and the rules for connectivity between and within populations.

Conceptually, a Population represents all cells of a particular type within the nucleus. When a population is created, the software initially specifies how many cells are represented and how to distribute specific properties across those cells. This allows populations to consist of cells that are not all identical, and is an important consideration when attempting to simulate biological processes. For example, an SGC population can describe 10,000 cells distributed uniformly across the tonotopic axis and evenly split between spontaneous rate groups. Initially, none of these 10,000 cells are actually created; rather, each cell exists as a virtual placeholder, and is only instantiated when it is explicitly requested or when it is required to satisfy the input requirements for another cell.

Populations are connected to each other in much the same way cells are, by invoking a connect method on the presynaptic population, with the postsynaptic population as an argument. Like the virtual cells, however, this connection does not create any synapses, but instead merely records the fact that one population of cells projects to another. Once the populations of interest are created and connected, the user then manually instantiates only the cells that they wish to record from, and the population provides a method that determines and creates the entire network of required presynaptic inputs.

Because populations manage the creation of synaptic connections between large groups of neurons, they are also responsible for ensuring that the appropriate patterns of connectivity are followed. For example, this allows us to ensure that bushy cells are automatically connected to auditory nerve fibers coming from a relatively narrow window across the tonotopic axis, whereas D-stellate cells integrate the same inputs across a broader window. Likewise, Population classes determine the convergence at each stage of the network and the cell-to-cell variability in convergence.

Data

One of the pitfalls we encountered while developing CNModel is that biophysical parameters (such as channel densities, synaptic strengths, and convergence numbers) that are written directly into the source code are difficult to track. In many cases, the provenance of each parameter may be inadequately documented, or it may be unclear whether a previously published result is represented in the code. To address this, we store all such parameters in human-readable tables that are separate from the Python source code but can still be accessed programmatically. The tables include annotations and references that define the provenance of the values for each parameter and which can indicate the level of confidence that might be placed on those values. The rationale behind using external human-readable tables is that the parameters of the model, such as the ion channel conductances, patterns of connections, synaptic strength and synapse kinetics, are all clearly specified in one location and easily evaluated, which helps remove any ambiguity and enforces documentation of the parameters. Where the data tables are incomplete, we have provided sensible placeholder values and made appropriate annotations. Future experiments will be needed to measure these properties.

Protocols and Acoustic Stimuli

A Protocol class provides support for various stimulation protocols such as responses to current injections, voltage clamp protocols on single cells and sounds. Sound stimuli are defined as subclasses of a Sound class. Each subclass of the Sound class defines the function for generating a sound waveform, but also provides a unique key that is used to store and retrieve auditory nerve spike trains that were generated with a particular stimulus and random number seed. Sound objects may be passed directly to SGC cells or SGC populations, and as needed, the necessary spike trains are automatically computed or, if the spike trains for a particular stimulus and random seed have already been computed, read from disk. This class currently implements functions for tone pips, noise, sinusoidal amplitude modulated tones and noise, and click trains.

Auditory nerve input

CNModel builds from the auditory periphery model developed by Zilany et al. (Zilany et al., 2014; Zilany et al., 2009). The periphery model takes waveform inputs (from the Sound class) and converts them into spike trains for auditory nerve fibers of a specific CF and SR group. Because the periphery model was originally developed in MATLAB®, CNModel uses a Python implementation of the periphery model called cochlea (Rudnicki et al., 2015). Alternatively, CNModel can invoke the original Zilany et al. model using a Python-to-MATLAB® bridge that runs in a background process..

Bypassing MATLAB® shortens computation time for the auditory nerve spike trains, which can be significant if the spike trains for a particular stimulus set and random number seed have not already been computed.

Unit Testing

The goal of this structured approach, which follows the form of the biology, is to ultimately simplify the top-level organization of the model and to help ensure some level of correctness in implementations. To further help with this, a group of unit tests has been developed to determine the correct operation of low-level operations, and to reproduce known data from the literature in the context of the present model. Several example simulations are available to demonstrate the capabilities of the model. Some additional tools are also available, including a set of routines that provide simple visualization of cells, their decoration patterns, membrane voltage changes with time, and display of the results of network simulations.

CNModel attempts to reproduce a large and complex set of published (and unpublished) observations. The complexity of the model makes it highly sensitive to changes in its physiological parameters. Small modifications to the code or underlying databases may have unexpected (and sometimes unnoticed) consequences in the output of the model. To help combat this unavoidable fragility, CNModel includes a battery of unit tests that are used to ensure the model output is stable across modifications and platforms, and that it does reproduce our target observations within reasonable limits for known cases. As such, any modification to the individual elements of the model should usually be followed soon after by running the unit tests.

The reference test results are stored in a database, which can be audited and updated when a particular model is considered to be stable. Stable parameter sets and results should be committed to a long-term repository. It is up to the user to perform the validation, and to add new tests for new models. The current suite (summarized in Table 1) matches published models of guinea pig ventral cochlear nucleus (VCN) cells (Rothman and Manis, 2003b), a rat pyramidal cell model (Kanold and Manis, 2001), and models from mouse VCN (Xie and Manis, 2013). Reference test results are also available and stored for the implementations of the ad-hoc model cells (guinea pig octopus cell, mouse cartwheel and tuberculoventral cells, and spiral ganglion cells). The synapse models for each cell type are also available. The list of reference test results can be easily updated or expanded as needed.

Table 1.

Base model cells implemented in the library in CNModel.

Species Cell type	Guinea pig	Mouse	Rat
Bushy	RM03, type IIm, type II-I	XM13, mGBC
T-Stellate	RM03, Type 1-t, Type 1-c	XM13
D-Stellate	RM03, type I-II	XM13
Octopus	RM03, “I-o” (ad hoc)
Pyramidal			KM01
Cartwheel		Ad-hoc
Tuberculoventral		Ad-hoc
SGC		Ad-hoc, LMD14

RM03: Rothman and Manis, 2003c; XM13: Xie and Manis, 2013; mGBC: modified mouse globular bushy cell; KM01: Kanold and Manis, 2001; LMD14: Liu et al., 2014. Responses of most of these models to current injection are shown in Figure 4.

Tracking of model parameters across runs is another area where careful record keeping is needed to ensure reproducibility. There are two ways to accomplish this. One way is to provide an output that reports all of the variables of a specific simulation run. We think that this latter approach is more error prone, as it depends on all of the variables being both accessible and included in the report. Although in CNModel we have collected the majority of the parameters in data tables as already descdribed, and other parameters are fixed in the NEURON NMODL files (which are compiled), there can be parameters that the user may adjust in a given simulation that are not readily captured this way. However, maintaining the individual simulations under a version control program is probably the best approach. An example of this is the package Sumatra (Davison et al., 2017), which works with several different version control systems, and is designed specifically to address issues related to reproducibility of simulations and their workflow. We have successfully performed limited tests of CNModel with Sumatra.

Platform

Because CNModel is coded in Python (V2.7) using standard libraries, it can run on any system that supports Python and NEURON. The simulations shown in this paper were run on a 3GHz 8 core Mac Pro with 16 GB (2013, running OSX 10.11.6), on a 2.13GHz Intel Core 2 Duo MacBook Air with 4 GB memory (2010, running OSX 10.11.6) and on a 3.5 GHz Intel Core i7 Macbook Pro with 16GB memory (2017, running OSX 10.13.1). and a Sony Vaio, with 8GB memory and an Intel Core I7–4500U processor, running Linux. Development and testing was performed under OSX and Ubuntu Linux. As described in the online documentation and the github repository (http://www.github.com/cnmodel), CNModel depends on numpy (1.11), scipy (0.19), PyQt4 (4.11.4), PyQtGraph (0.10), lmfit (0.9.3), matplotlib (2.0 or 1.5) and a Python-linked version of NEURON (7.4 or later). A C compiler is needed to compile mechanisms for NEURON. The auditory periphery model cochlea should be installed according to instructions (https://github.com/mrkrd/cochlea). Alternatively, the original model from Zilany et al. (2014) can be installed if MATLAB® is available.. We have also included the current version of the github repository (tagged as “hearing-research-2017”) as Supplementary Materials for archival reference; however, we recommend cloning CNModel from the repository. A shell script that generates the model data shown in Figures 2–7 in this paper is included in the examples subdirectory of the repository.

Figure 2.

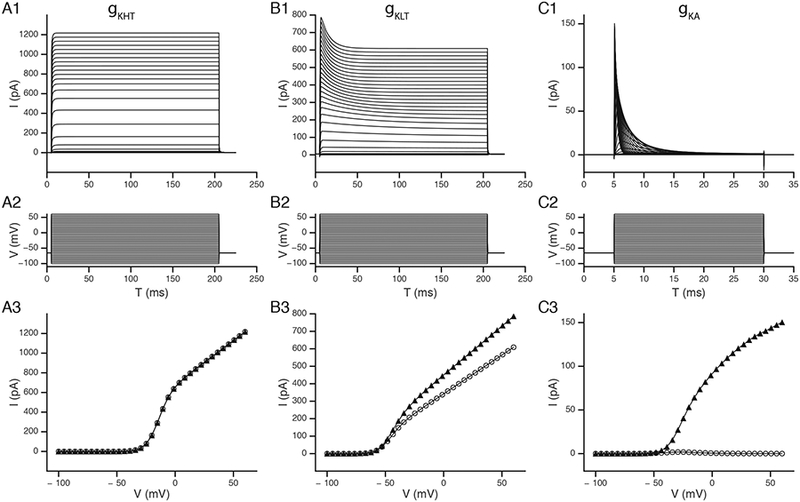
Examples of ion channel currents as implemented at the NEURON level. The voltage dependent currents as measured in voltage clamp from a simple point cell were used to demonstrate the high-voltage activated (gKHT; panels A1), low-voltage activated (gKLT; panel B1) and transient potassium (gKA; panel C1) currents from the model of Rothman and Manis (2003c). The middle row (A2, B2, C2) shows the command potentials, and the lower row (A3, B3, C3) shows the steady state (open circles) and maximum (solid triangles) currents for each type of conductance.

Results

We summarize the results from the model at different levels by showing examples of the usage of the platform and its performance on some basic tasks, followed by some more complex simulations. All simulations described below can be replicated by running the examples/figures script included in the source code.

Conductances

The most detailed models of ion channels and point cell representations are for the bushy and stellate cells of the guinea pig VCN. Figure 2 summarizes the currents generated by the 3 principal potassium currents measured in these cells as implemented in point cells under voltage clamp, reproducing our previous measurements (Rothman and Manis, 2003a). Each column shows, from top to bottom, a set of voltage clamp traces (Figure 2 A1, B1, C1), the command waveforms (Figure 2 A2, B2, C2), and the voltage dependence of the peak and steady-state currents (Figure 2 A3, B3, C3). Figure 2A1 shows traces of the high-threshold potassium conductance, with activation above −40 mV (Figure 2A3). Figure 2B1 shows the low-voltage activated (KLT) conductance, which activates near −60 mV (Figure 2B3). This conductance also shows a slow voltage-dependent inactivation, indicated by the time-dependent decrease in the currents which is faster and more prominent at the most positive command voltages. Figure 2C1 shows the activation and inactivation of a fast transient potassium conductance that was seen in some VCN neurons (Rothman and Manis, 2003b). Although the steady-state currents (measured 20–25 msec after the start of the step, Figure 2A3) are small, a very small “window” current is visible between −50 and −20 mV, corresponding to the voltages where there is overlap in the activation and inactivation functions.

Intrinsic Firing Patterns

Figure 3 summarizes the intrinsic firing patterns of the library of point model cells included in CNModel. Figure 3A-F shows traces from the original models (Rothman and Manis, 2003a) which are based on kinetic data measured from guinea pig cells at 22C. Figure 3F is a point octopus cell model, which has an elevated low-voltage activated potassium conductance. Figure 3G and H show mouse bushy and T-stellate models (Xie and Manis, 2013) at 34°C. Figure 3I shows a D-stellate cell model that is similar to the model shown in Figure 3C. This model includes a small amount of the low-voltage activated potassium conductance, which limits firing to only onset action potentials near threshold (Xie and Manis, 2017a). Figure 3J shows the rat DCN pyramidal cell model (Kanold and Manis, 2001). Additional point models that reproduce the bursting firing pattern of cartwheel cells (Figure 3K) and the regular firing of tuberculoventral cells (Figure 3L) have also been implemented. The cartwheel cell model is derived from a Purkinje cell model (Khaliq et al., 2003), with the conductances tuned to more closely replicate the mixed bursting and regular firing of DCN cartwheel cells. The tuberculoventral cell model is derived from the VCN T-stellate cell model, but uses a modified sodium channel that includes inter-channel gating cooperativity (Huang et al., 2012; Ilin et al., 2013) to increase the rate of activation and enable higher firing rates. The sodium and delayed-rectifier channel conductances for the tuberculoventral cell model were adjusted by exploring a large parameter space that was constrained against the firing rate at +600 pA, whereas the input resistance and the membrane time constant were adjusted by exploring the subthreshold voltage space while adjusting the leak and hyperpolarization-activated conductance. The constraining data were taken from the data from mouse tuberculoventral cells (Kuo et al., 2012). Figure 3G and H show two models for spiral ganglion cells. Both models are derived from the bushy cell model in Figure 3G (at 34C), and reflect the firing patterns of mouse SGCs in vitro (Liu et al., 2014; Mo et al., 2002). For these two point models, the hyperpolarization-activated conductance was replaced with either the kinetic model for apical SGCs, or for SGCs from the middle and basal cochlear regions (Liu et al., 2014).

Figure 3.

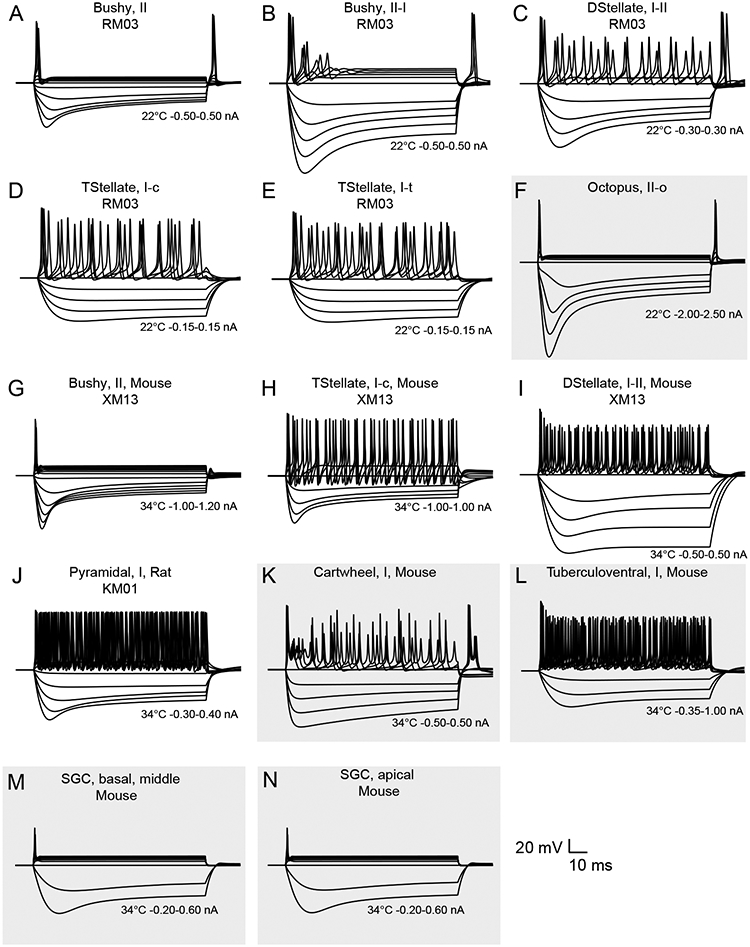
Intrinsic excitability of cells implemented in CNModel. Panels A-E are from the models of Rothman and Manis (2003c). Panel F shows an “Octopus, II-o” cell, which is a variation on the bushy cell, with a modified hyperpolarization activated current, and an elevated low-voltage activated potassium conductance. Simulations in A-F were all run at 22 °C. Panels G-I are simulations based on mouse cochlear nucleus neurons from Xie and Manis (2013). Panels J-L show DCN cell models. The simulation in J is from the model of pyramidal cells in rat (Kanold and Manis, 2001). K and L are ad-hoc representations constrained by current-clamp observations as described in the text. Panels M and N are spiral ganglion cell models, based on the mouse bushy cell model (G), but with the hyperpolarization-activated K current from Liu et al. (2014) for basal-middle (M) SGCs and apical (N) SGCs. Models in G-N were all run at 34 °C. Inset scale bar applies to all voltage traces. Temperature and current ranges are shown beneath the traces. Previously unpublished, ad-hoc models, are shown on a grey background.

Multiple-release site synapse

The synapses from the auditory nerve onto bushy cells, known as the endbulbs of Held (Manis et al., 2011) have multiple release sites. To better simulate the stochastic behavior of these synapses, and their release dynamics, we developed a NEURON mechanism that handles the release process (Xie and Manis, 2013). This mechanism was inspired by an earlier model of release at the calyx of Held in the medial nucleus of the trapezoid body (Graham et al., 2001). Briefly, this mechanism provides independent probabilistic release at each presynaptic site within the terminal, where the probability over time is governed by the history of activity of the terminal, using a robust kinetic description (Dittman et al., 2000). The parameters were estimated from simultaneous fits of the model to experimental data taken at stimulus frequencies from 50 to 400 Hz, which included recovery intervals after the stimuli out to > 2 seconds. The kinetics currently implemented are those for endbulbs of Held in the mouse VCN (Xie and Manis, 2013). In addition, a simple time-dependent latency mechanism is included, to replicate the slight increase in latency observed experimentally during regular trains of activity.

Figure 4 illustrates the synaptic currents under voltage clamp as measured in a model bushy cell as produced by the multisite model during a 100 Hz stimulus train applied to a presynaptic SGC. The simulation includes the postsynaptic receptor model that includes desensitization. Figure 4A shows the presynaptic voltage waveforms in the SGC in response to the train of current pulses. Figure 4B shows the train of EPSCs in the bushy cell, for 10 repeated trials (overlapped), illustrating some of the variability in the response amplitude. In Figure 4C, the latency to 20% and to 80% of the peak amplitude of the EPSCs are plotted for a single trial. Note that the latency slightly increases through the train, as a result of the time-dependent latency factor in the release mechanism. Figure 4D plots the EPSC width at half-height during the train, again for a single trial. Figure 4E shows the rise time (measured as the time from 20–80% of peak amplitude) fluctuations during the train. The rise time varies because the release latency for each site includes a small amount of jitter. This jitter is illustrated for all of the individual events across all trials in Figure 4F. The variable release latency for each site is drawn from a log-normal distribution according to the measurement of individual release events under conditions of low release probability (Isaacson and Walmsley, 1995). In addition, a time-dependent shift in the mean latency (visible in Figure 4F) can be included in the model, to mimic a similar shift seen experimentally. The histogram in Figure 4G shows the marginal distribution of individual release latencies in Figure 4F, across all trials.

Figure 4.

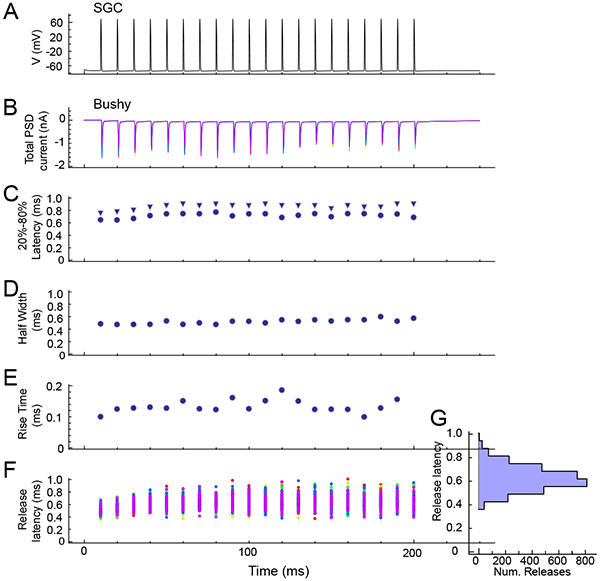
Multisite release model. Simulations are shown that combine a “dummy” SGC with a single multisite release synapse and a postsynaptic mouse bushy cell. A. A 100 Hz regular stimulus train was applied to the SGC. B. Synaptic currents in the bushy cell in voltage clamp (5 trials superimposed). Variability in the amplitude of the currents results from a combination of the stochastic release at individual sites, and variability in the release amplitude. C. 20% (circles) and 80% (triangles) of peak amplitude latency for events in a single trial. D. Width of EPSCs at half peak amplitude across a single trial. E. Measured rise-time of EPSCs for a single trial. F. Release latency for each active site across all trials (each trial is in a different color). Note the slight increase in latency (also visible in C) through the train, which is generated by including a time dependent latency shift in the model (see text). G. Marginal histogram of release latencies.

The multisite mechanism is computationally intensive, and may not be suitable for use in large scale simulations. However, it can be useful when attempting to replicate in vitro experimental data, and to understand the contribution of probabilistic release in auditory coding. As an alternative, the standard Exp2Syn mechanism from NEURON is also available, which provides fast, but deterministic, synaptic conductances, and should be preferred for most network simulations.

Channel Decoration

One goal of CNModel was to be able to simulate cells with their full morphology. Figure 5A shows a reconstructed mouse bushy cell. In addition to the soma and dendrites, a short portion of the axon hillock and initial segment is visible. After decorating the cell with ion channels (according to the densities described in Table 2), a set of responses to current injection were simulated (Figure 5B). Responses to current injections are similar to those of the point model (Figure 3), although in this simulation, the current-voltage relationship is more symmetrical around rest.

Figure 5.

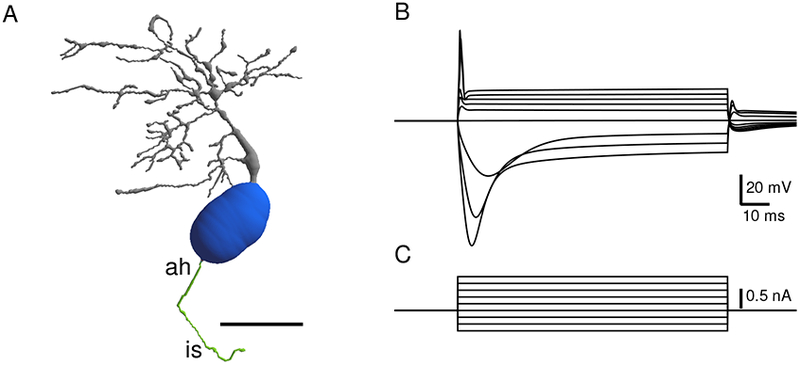
Excitability of reconstructed bushy neuron. A. Reconstruction of a fluorescently labeled mouse bushy cell from the data set of Campagnola and Manis, (2014). The cell was filled with the fluorescent dye AlexaFluor 488, and reconstructed from a multiphoton image stack using Neuromanitc (Myatt et al., 2012). The cell was then decorated with channels as indicated in Table 2. Grey: Dendrites, blue: soma, green: axon hillock (ah) and initial segment (is). Scale bar: 20 microns. B. Traces in response to current injections at the soma, showing canonical bushy cell response (parameters of channel decoration are shown in Table 1). C. Current steps for panel B.

Table 2:

Mouse bushy cell model used for cell decoration in Figure 4. Nominal conductance values for each type of channel in the bushy cell model are shown in the first row, based on scaling the total somatic conductance in the Xie and Manis (2013) model to somatic surface area.

Conductance	Na	KHT	KLT	Ih	leak
Reference value (mS/cm2)	34.6	2.01	2.77	1.04	0.069
Soma	0.65*	1.5	1.5	1.0	1.0
AH	2.0	3.0	1.0	0	1.0
IS	1.5	2.0	2.0	0.5	1.0
Dendrites	0.1	1.0	1.0	0.5	0.5
Dendrite spatial distribution	100 μm	100 μm	100 μm	None	None

Na: sodium channel conductance, KHT: high threshold potassium channel conductance, KLT: Low voltage activated potassium channel conductance, Ih: hyperpolarization activated cation channel conductance, leak: ohmic leak conductance. The conductances in each type of compartment (soma, axon hillock (AH), initial segment (IS) and dendrites) are then scaled by the multiplier in the subsequent rows. The conductances in the dendrite were further scaled linearly with distance along the path from the junction with the soma to a value of 0 at the distance indicated in Dendrite spatial distribution. The somatic scaling for the Na conductance (*) is based on Yang et al., 2016.

Effects of varying conductance levels on bushy cell responses to cur-rent and auditory nerve input

Cao and Oertel (2011) reported that across different strains of mice, and across different types of VCN cells, the magnitudes of the g_H and low-voltage activated conductances covaried, such that strains that exhibited a lower density of g_H also exhibited a lower density of g_KLT. This interesting observation suggests a co-regulation of the expression levels of these two conductances, which may also be linked to maintenance of a target cell resting potential (Cao and Oertel, 2017). Variations in the magnitudes of these two conductances would also be expected to influence excitability and synaptic integration. We therefore examined how variation of g_H and g_KLT affects the intrinsic excitability of the cells and spontaneous firing, and driven firing rates. For these simulations, we used the mouse bushy cell model (Figure 3G), with 3 multisite, stochastic auditory nerve inputs (endbulbs) at a fixed conductance (each synapse had an AMPA receptor conductance of 21.1 nS, with 100 release sites for each endbulb), with no synaptic depression. The results of co-varying the strength of g_KLT and g_H from 0.25 to 2 times the nominal values (conductance ratio relative to the standard at 1.0, gR) are shown in Figure 6. Figure 6A shows responses to current injections. At the highest conductance levels (g_R > 1), the spike threshold is elevated; however, the cells still have a canonical single-spike response to the current steps. At lower levels of g_H and g_KLT (gR < 0.5), spike threshold is lowered, and at the lowest level (gR = 0.25), the cell shows membrane potential oscillations following the first spike. Spike threshold was a monotonically increasing function of g_R (Figure 6B). Next, we generated responses to high-frequency (4 kHz) tones in high-SR auditory nerve fibers at 50 dB SPL in the AN model. Figure 6C shows the membrane voltage traces in the bushy cell model for single trials with different amounts of gH and g_KLT. At the lowest conductance levels, the cell fires in response to spontaneous EPSPs, but during the tone burst, when the EPSP rate increases, the membrane voltage depolarizes and the cell fails to generate spikes (defined by simple threshold detection as events crossing −20 mV with a positive slope), as the depolarization prevents removal of inactivation from the sodium channels. As the co-varied conductances increase (gR), spike repolarization enables firing through the stimulus, although the amplitude of the EPSPs also decreases because of decreased input resistance, and the firing rate decreases. PSTHs for 25 trials in response to the tone pip are shown in Figure 6D. This simulation shows that over a range of conductance values, from half to nearly twice the reference values, that the firing patterns and voltage response to current injection of the bushy cell are qualitatively similar. The PSTH resembles the patterns seen in mouse bushy cells, including a precisely timed first spike, followed by a “notch” (Roos and May, 2012). The spontaneous and the driven firing rates are a non-monotonic function of g_R (Figure 6E). At the lowest conductance level (g_R = 0.25), the cell has a very low spontaneous rate and a low driven firing rate during the stimulus (due to depolarization block). At the higher conductance levels (g_R > 1.5; see Figure 6E), the spontaneous and driven firing rates also decrease as the EPSP frequently fails to reach threshold. In this set of simulations, the strength of the synaptic input was held constant. However, some of the effects of varying the ionic conductances on the spontaneous and driven rates could be compensated by adjusting the synaptic strength.

Figure 6.

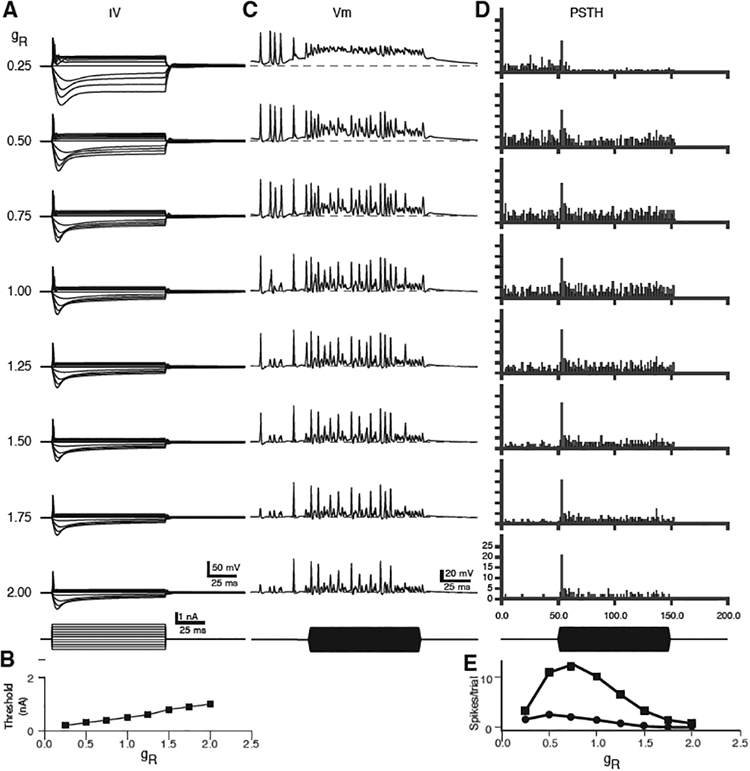
Model responses in bushy cells with varying levels of the low-voltage activated potassium conductance and the hyperpolarization activated cation conductance. g_KLT and g_H were varied together from 25% of their nominal values (g_R = 0.25) to 200% (g_R =2.0). A. Summary of responses to current pulses. B. Spike thresholds in nA for each level of g_R. C. Responses to 3 SGC inputs (endbulbs, 100 sites each) at different values of g_R. The SGC inputs were computed responses to 4 kHz tones in high-SR auditory nerve fibers at 50 dB SPL from the AN model. D. Post-stimulus time histograms (PSTH, 1 ms bin width) of cumulative spikes over 25 stimulus trials. E. Summary of spontaneous (circles) and driven (squares) spike counts for the PSTHs shown in D, as a function of gR. Calibration bars in bottom row of the left and middle columns apply to all traces in those columns. Values of g_R for each row in A also apply to traces in C and PSTHs in D.

Populations and Network Simulations

One of our ultimate goals when developing this platform was to simulate the activity of networks of neurons in the cochlear nucleus. For this purpose, the Population class provides tools for instantiating a network of cells that are connected to a particular target cell. Figure 7 illustrates how this class is used, and the kinds of results that can be obtained. The left panel shows a network that resulted from creating four populations and selecting a single bushy cell with a CF of 16 kHz. Once the selected bushy cell is created, the Population class resolves the pattern(s) of input cells and connections required to simulate the target cell. In this case, the network includes the 3 SGC endbulb inputs to the bushy cell, and generates populations of tuberculoventral neurons (Campagnola and Manis, 2014; Muniak and Ryugo, 2014; Wickesberg and Oertel, 1988) and D-Stellate neurons (Campagnola and Manis, 2014) that provide input to that bushy cell. For each of these cells, additional inputs were drawn from the SGC population as needed. Further resolving the required inputs would have recruited additional D-Stellate cells that contact the tuberculoventral cells (Arnott et al., 2004; Nelken and Young, 1994; Oertel and Wu, 1989), however those connections were not activated in this simulation. The middle column shows frequency response areas for three of the cochlear nucleus cells measured in 10-dB steps across the range from 4–32 kHz in 1/8 octave steps, averaged across 5 trials. Tonotopic convergence ranges are described in the CNModel data tables as standard deviations (σ) for a log-normal distribution scaled to the CF of the postsynaptic cell. Some of these values were determined from our prior glutamate uncaging studies (Campagnola and Manis, 2014). For example, in this simulation, the D-Stellate cells have a wide frequency response area, as their convergence from SGCs occurs across 0.4 σ, as compared to 0.1 σ for the tuberculoventral cells, and 0.05 σ for the bushy cell. On the right are shown a membrane potential trace for each cell type for the same frequency and intensity, just below the 16kHz CF, as indicated by the white box in the middle column. Shown beneath the traces are the spike times for every cell in the model that provided input to the target cell. Although there are several details of this simulation that should be explored further (for example, the distribution of spontaneous rates of the SGC inputs to different cells, incorporation of the D-Stellate input to the tuberculoventral cells, the relative strengths of inhibitory synaptic inputs), this simulation shows how CNModel can be used to study the responses and interactions among populations of cells in the cochlear nucleus in response to acoustic stimulation.

Figure 7.

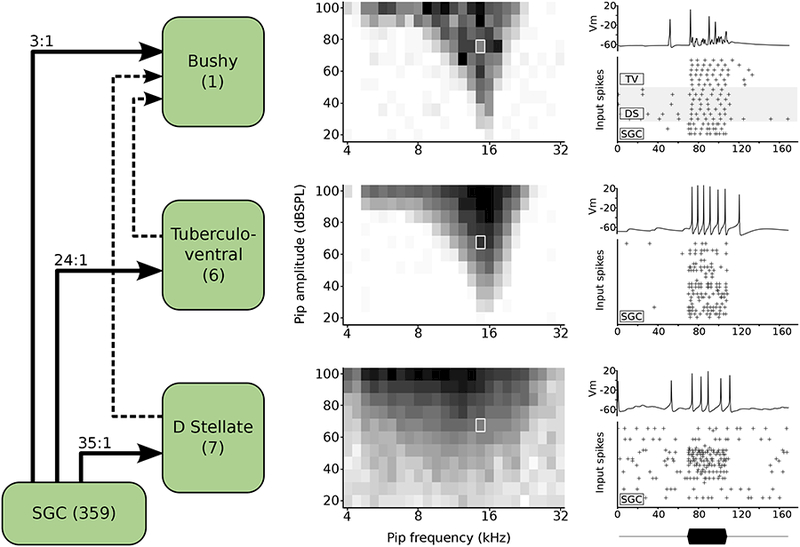
Model response to tone pips of varying frequency and intensity. Left: circuit schematic in a model of a single bushy cell and its synaptic inputs. The bushy cell has 3 medium-spontaneous rate (SR) SGC inputs, 6 TV inputs, and 7 DS inputs. Each DS cell receives 35 SGC inputs (selected from all SR groups), and each TV cell receives 24 SGC inputs (selected from low- and medium SR groups). For simplicity in this simulation, the TV cells receive inputs from the SGCs, but not from DS cells. Center column: response maps for a bushy (top), TV (middle), and DS (bottom) cell showing the firing rate (average of 5 trials) for each combination of sound level and frequency. Darker shades indicate higher firing rates, and each map is normalized to its highest firing rate. Right: A representative membrane voltage trace taken from a single trial (indicated by white rectangle in the center panel at 14,672 kHz and 76 dB SPL) and the corresponding presynaptic spike input times for each input source to that cell. The envelope of the tone pip is shown at bottom.

Timing

Here we summarize some timing of runs of the models shown in the figures. Except for Figure 7, the times are all for a 3.5 GHz i7 computer (see Methods for full descriptions of the computers used). Traces for Figure 2 required 0.76s for g_KLT, 0.71s for g_KHT and 0.34s for g_KA (without parallel processing, but including plotting of the traces). The generation of traces for all cells in Figure 3 was completed in 18.4s, using parallel processing. The stochastic multisite synapse simulations shown in Figure 4 completed in 7.1s for 5 repetitions, compared to 0.14s for a simple double-exponential deterministic synapse model. For the reconstructed cell in Figure 5, the complete current-voltage relationship completed in 20.3s, without parallel processing. Figure 6A required 3.1s (parallel processing), whereas Figure 6B required 472 s (parallel processing with precomputed AN spike trains). Figure 7 took approximately 9 hours for 5 repetitions on the Sony Vaio computer.

Discussion

As a computational platform, CNModel is not specifically designed to address a particular set of problems, but rather to facilitate the exploration of ideas using a robust framework while providing significant flexibility in model construction. As such, new data on mechanisms or connectivity can and should be incorporated as needed. In addition, the platform includes components that allow simulations to be run at several levels of complexity (point cells, “stick” cells, or morphologically realistic cells; stochastic synapses or deterministic synapses with or without activity-dependent dynamics). This provides a pathway for development, starting from simpler mechanisms and evolving to more complex and detailed simulations, that can facilitate confidence in the simulation results and allow the parameter space to be explored and constrained in a logical and sequential manner. Thus, we hope that this platform can be extended and facilitate general efforts to model specific functions in the auditory pathway.

In the remainder of this discussion, we address a variety of issues that must be considered when using this platform (or any other) to explore and make predictions about nervous system processing. Much of this discussion focusses on considerations related to the model parameters as abstracted from the literature. We preface this section by echoing how the limitations of our knowledge affect attempts at “realistic modeling” (Almog and Korngreen, 2016). In particular, quantitative information about many aspects of connectivity is lacking in the cochlear nucleus, and there is virtually no information about dendritic ion channel densities, although such measurements have been elegantly made in the medial superior olive (Scott et al., 2007; Winters et al., 2017). However, the present platform, in conjunction with detailed morphological structural information for single cells, can be used to explore specific questions and perhaps inform experimental strategies.

Decisions regarding model parameters.

Detailed electrophysiological models inherently have a large number of parameters, some of which are well constrained by data from the literature, and some of which must be determined by inspection, parameter space exploration, or by making assumptions.

Picking the appropriate parameters is critical when building models whose results intended to support existing data or generate new hypotheses. There are a number of limitations regarding the availability of specific parameters that must be considered. In general, models should be constructed through a process that builds from the known and measured biophysics and connectivity, in order to provide appropriate constraints and mimic the system under consideration. This might be viewed as a “forward” problem, in the sense that knowledge of the expected behavior is not implicitly incorporated into the selection of the parameters. On the other hand, when specific parameters are not yet known, or cannot be accurately determined from experimental measurements, a selective and thoughtful exploration of the parameter space(s) for multiple variables may be necessary to bring the model in compliance with other experimental measurements (for example, tuning potassium or sodium conductance levels to achieve appropriate spike thresholds, maximal firing rates, spike widths, and spike adaptation rate). Most of these factors should be approximately correct if a model is initially constructed based on careful and technically sound measurements of channel densities and kinetics. Other more advanced methods also exist for setting channel conductances. For example, genetic algorithms, in which an evolutionary approach is taken to select the best fit populations of model cells created with a range of conductance levels, can be used to find parameter sets that best align model responses to current pulses against specific examples of spike patterns and subthreshold voltages measured from experimental results (Druckmann, 2007; Druckmann et al., 2008). However, it is also important to recognize that multiple sets of parameters can often provide a satisfactory replication of a specific discharge pattern (Gjorgjieva et al., 2016; Schulz et al., 2006). In addition, although cochlear nucleus cells are often treated as canonical and distinct classes, in part based on their morphology and projections, their discharge patterns appear to form a continuum (Typlt et al., 2012), which may reflect variations in intrinsic excitability (Ahn et al., 2014) and the strengths of some of the conductances (Figure 5 and Rothman and Manis (2003c)).

There are some important limitations with regard to the data that is available to constrain the construction of models. First, the kinetic measurements for ion channels are of necessity made under “point” voltage clamp, that is, with a single electrode usually located on the cell soma. Unless the recorded cell is a small sphere without processes, the voltage clamp control of distal dendritic processes and axonal arbors is poor (Poleg-Polsky and Diamond, 2011; Spruston et al., 1993; Williams and Mitchell, 2008), and can distort the measured current time course and amplitude, even when single classes of channels are pharmacologically isolated. The most accurate measurements of voltage and time-dependent channel activation are made on isolated cells that are shorn of processes (Manis and Marx, 1991; Rothman and Manis, 2003a; Rothman and Manis, 2003c), or perhaps from outside-out patches that are pulled from specific regions of the cell membrane (Harty and Manis, 1998; Kanold and Manis, 1999; Raman and Trussell, 1992). However, because such measurements sample a small region of the membrane, and because channels and receptors are often clustered, many measurements are needed to estimate the channel density. Furthermore, channels in patches may be subject to physical forces from abnormal membrane curvature and tension (Hammami et al., 2009; Suchyna et al., 2009), or from disruption of the cellular protein scaffold that anchors channels, and these can affect channel gating. Measurements from intact cells (such as in brain slices) can be used to reveal the presence of different classes of channels, and can be used to derive estimates of channel densities for perisomatic channels. However, intact cells are suboptimal for measuring channel kinetics. Ultimately, the implementation of specific channel mechanisms relies on the precision of kinetic and conductance measurements. Because presently available techniques are limited in their ability to provide accurate measurements, exploration of the sensitivity of the models to variations in channel densities and kinetics, and comparison with experimentally-obtained intrinsic firing patterns of the cells are essential steps in constructing useful models.

Neurotransmitter receptor and presynaptic mechanisms (dynamics) are affected by many of the same experimental constraints. Fortunately, a number of carefully constructed models of receptors have been devised that account for binding, gating, desensitization and deactivation rates, largely based on kinetics measured in outside-out patches, and these are easily adapted for use in models when coupled with separate measurements of total synaptic conductances. One of the major issues in the implementation of models of presynaptic mechanisms is the use of high calcium concentrations in brain slice experiments. Originally, solutions with a high (2–2.5 mM) extracellular calcium concentration (and comparable magnesium) was adopted in hippocampal slice preparations, as it was found that recordings were more stable over time than in the presence of lower calcium concentrations (Gibson and McIlwain, 1965). However, as revealed from studies at the calyx of Held (Lorteije et al., 2009), these concentrations bias estimates of the resting release probability upward, and increase the visibility of synaptic depression relative to the situation in vivo, where calcium and magnesium in the extracellular space are generally thought to be lower (Borst, 2010). Comparisons at AN synapses onto VCN multipolar cells show that depression during high presynaptic rates is still present, though slightly reduced, at lower calcium concentrations (Xie and Manis, 2017a). Simulations indicate that modest depression is consistent with the experimentally measured entrainment in bushy cells over the range of convergence seen in cat (Rudnicki and Hemmert, 2017). In the future, measurements of release probability and synaptic dynamics should be made under conditions more closely approximating the normal extracellular divalent ion levels.

Temperature

The CNModel platform provides implementations of many basic mechanisms. Most of these have been subject to careful kinetic measurements at a single temperature (usually either 22°C or 33–34°C), but neither the kinetic variation of the rate constants nor the open conductance have been evaluated as a function of temperature. For example, the original measurements for the VCN potassium channels were obtained at 22°C(Manis and Marx, 1991; Rothman and Manis, 2003c). Based on other studies in the literature, scaling to 38°C was suggested to have a Q10 for rates of 3 and for conductance of 2 (Rothman and Manis, 2003b), but there is no experimental data to directly support this scaling. The maximal conductance for some channels has been measured in mouse (Cao et al., 2007) at 34°C, but kinetic measurements for the channel activation rates were not made. More detailed studies of the temperature dependence of conductances in the octopus cells have been made (Cao and Oertel, 2005), and the variations in the temperature dependence between conductances suggest that some care must be used when attempting to scale rates and conductance values in models.

Because temperature is such an important factor in the time course of ion channel kinetics, receptor and synaptic conductances, and synaptic dynamics, and because measurements have been made at multiple temperatures, CNModel limits the temperature range at which specific mechanisms can be used or combined. Each cell model or synaptic mechanism includes a read-only parameter that is set when the model is instantiated, and that value is checked against the specified run temperature. this minimizes the chance that mechanisms derived from measurements at different temperatures will be mixed together in the construction of a particular model.

Constraints from in vivo data

An important goal for any auditory neuron model is to reproduce the in vivo responses to sound with reasonable fidelity. A number of in vivo measurements can be used to constrain cellular models at different levels of analysis. For example, Rothman et al. (1993) used data from cat VCN neurons to compute the spike hazard function (probability of a spike occurring in time after a previous spike). The hazard function in turn is dependent on the absolute and relative refractory periods for spikes. In the construction of that model, we found that the standard Hodgkin-Huxley sodium channel, even when scaled to 38°C, had a slow recovery from inactivation that limited spike rates and made the refractory period too long. As the recovery from inactivation is voltage-dependent, it was evident that the inactivation rate near the resting potential was too slow. Thus, the sodium channel was adjusted so that it had a very fast recovery from inactivation for voltages just below the resting potential. That model works well for VCN neurons, but the spike shape does not accurately recapitulate the shapes of spikes recorded in vitro. Recent measurements of sodium channel voltage-dependence in bushy cells are a good step towards the development of better sodium channel models for some cochlear nucleus neurons (Yang et al., 2016).

Additional measures from in vivo data, such as latency, regularity (Young et al., 1988), adaptation to tone stimuli, phase locking and envelope locking and forward masking require that the neurons be embedded in a circuit that includes at least the auditory nerve input, and likely local inhibitory or excitatory connections. Many of these measurements are likely to depend on the convergence of auditory nerve fibers and the locations of those synapses on the cell because of dendritic filtering (White et al., 1994), as well as on the magnitude and time course of synaptic inhibition. We have not yet explored these factors in the current framework. One limitation is that although the auditory nerve responses to sound are statistically similar between the well-studied cat and mouse (Taberner and Liberman, 2005), currently we have only limited quantitative data for comparison for cochlear nucleus neurons in the mouse (Kopp-Scheinpflug et al., 2003; Ma and Brenowitz, 2012; Portfors and Roberts, 2007; Roos and May, 2012).

Species

Measurements that can provide data for cochlear nucleus modeling come primarily from mouse, guinea pig, and rat, along with more qualitative data from gerbils. CNModel currently incorporates detailed mechanisms from guinea pig and mouse studies. Models derived for one species, which may be constrained by specific target model behavior, may not easily apply to another species. For example, the magnitudes of the potassium conductances measured from isolated cells in guinea pig (Manis and Marx, 1991; Rothman and Manis, 2003c) are substantially larger than those measured in intact cells in brain slices in mouse (Cao and Oertel, 2011). In the process of developing our model for the VCN circuit (Xie and Manis, 2013), we found that the use of the conductance magnitude measurements made in guinea pigs failed to reproduce data obtained in current-clamp from the mouse cells. However, adjusting the conductances to those reported for the mouse allowed us to closely approximate the spike probabilities and jitter seen experimentally in response to auditory nerve stimulation in vitro. This points out the importance of scaling conductances and as appropriate for the species under investigation.

The time courses of activation, deactivation, inactivation and recovery from inactivation for the voltage-dependent conductances are also important to consider. These are experimentally more difficult to measure because of the difficulties with obtaining sufficiently rapid voltage clamp and the effects of voltage deviations on the activation state of channels that are remote (on dendrites or axons) from the recording site. The most accurate measurements are likely to be made from isolated cells, enucleated patches, or outside out patches, at room temperature. Defining the model and fitting kinetics is also a challenging exercise, although in the case of Hodgkin-Huxley style “macroscopic” models, a logical sequence of fitting against measurements at different voltages, recognizing the relationship between deactivation and activation kinetics, and careful attention to separation of kinetic components helps to achieve a useful model. Scaling to a useful temperature for a model is important, but accurate estimates for the temperature scaling is often lacking. In addition, as with the total conductance, there may also be species differences, or tonotopic differences. Such differences are important in the auditory system, having been shown in avian and mammalian cochlea.

Species with different hearing frequency ranges may have different densities of channels or kinetics of channels because the precision with which spikes are timed, or their synaptic convergence and synaptic integration requirements, are different. Mice, which have little hearing below 2 kHz, do not have much fine-structure phase locking. However, their central neurons in the inferior colliculus do phase lock to envelope information up to about 200 Hz (Geis and Borst, 2009; Walton et al., 2002), which suggests that neurons in the cochlear nucleus must have at least this range of locking to envelopes in the mouse. The spike time precision required to accomplish this does not require high levels of the low-voltage activated potassium channels. Employing lower channel densities may also reduce the energy requirements associated with a constant resting K⁺ leakage through those channels (discussed in Brownell and Manis (2014)). On the other hand, animals with good low-frequency hearing such as gerbils and guinea pigs, will need to have higher densities of g_KLT channels in order to minimize spike jitter, shorten refractory periods, and suppress supernumerary spikes (Gittelman and Tempel, 2006).

Summary

We have described a general-purpose platform for simulating the responses of single neurons and small neural networks, for single point cells and for morphologically reconstructed cells, in the cochlear nucleus, using biophysical mechanisms that are at least partially constrained by experimental measurements. This platform is easily extensible to include other cell types and patterns of connectivity, including binaural circuits, so it should not be considered to be limited to representing only neurons and synapses of the cochlear nucleus. In addition, in the construction of this platform, we recognize the need for additional measurements. Specific areas where data are lacking include quantitative measures of connectivity, spatial convergence patterns, and synaptic dynamics. Dendritic conductances also need to be evaluated for most cell types, although this is likely to be technically challenging. Nevertheless, we hope that this platform is useful in exploring the computational abilities and predicted sensory responses of neurons and networks of neurons in the auditory system.

Highlights.

1. A platform supporting biophysically-based modeling of cochlear nucleus neurons is presented.

2. The platform spans multiple levels, from channels to cell populations, and network connections.

3. Cells can be decorated with channels and synapses from morphological reconstructions.

4. The simulations can use auditory nerve models that convert sound waveforms to spike trains.

5. Example simulations, from channels through small spiking networks, are shown.